que resumen la transformación que será llevada a cabo de un sistema de coordenadas a otro.
Primero que nada, empecemos por visualizar a las cuatro variables (x,y,z,t) como un vector en cuatro dimensiones. Este vector tendría una representación en la forma de un vector renglón como la siguiente:
[x_y_z_t]
En realidad, este vector es una matriz que consta de un renglón y cuatro columnas, o sea es una matriz 1x4.
La representación matricial anterior dada a las cuatro variables de las ecuaciones de transformación de Lorentz adolece de un defecto: revuelve peras con manzanas. En efecto, las coordenadas x, y y z son longitudes medidas en metros, mientras que la cuarta coordenada es una dimensión medida en segundos. Pero esto tiene un remedio fácil, ya que todo lo que tenemos que hacer es multiplicar la cuarta coordenada por la constante universal absoluta que es la velocidad de la luz, por c, con lo cual obtenemos la coordenada ct que también está expresada en metros. De este modo, tenemos un vector renglón en el que todos sus componentes son peras (o manzanas):
[x_y_z_ct]
Repasemos ahora las ecuaciones de transformación de Lorentz:
____x = γ(x’ + Vt’)
____y = y’
____z = z’
____t = γ(t’ + Vx’/c²)
A continuación reescribiremos estas ecuaciones de transformación para preparar el sistema para su representación matricial, multiplicando la cuarta coordenada (la del tiempo) por la constante absoluta universal que es la velocidad de la luz c con la finalidad de que el vector de cuatro componentes a ser transformado de un sistema de referencia a otro contenga las cuatro coordenadas en dimensiones de metros:
____x = γx’ + 0y’ + 0z’ + γ(V/c) ct’
____y = 0γx’ + 1y’ + 0z’ + 0(V/c) ct’
____z = 0γx’ + 0y’ + 1z’ + 0(V/c) ct’
____ct = γ(V/c) x’ + 0cy’ + 0cz’ + γct’
Para aquellos con alguna experiencia previa en matrices el arreglo rectangular de la representación matricial requerida casi salta a la vista, ya que lo que queremos es convertir el vector [x’, y’, z’, ct’] al vector [x, y, z, ct], o sea:
[x’, y’, z’, ct’] → [x, y, z, ct]
Si hacemos las siguientes designaciones:
A = [x, y, z, ct]
A’ = [x’, y’, z’, ct’]
A’ = [x’, y’, z’, ct’]
entonces lo que estamos buscando es un operador Λ que aplicado sobre el vector A lo transforme al vector A’. En notación matricial (el operador usualmente se escribe a la izquierda del operando sobre el cual actúa, aunque hay algunos textos en los que por la falta de una convención universal se escribe primero el operando que va a ser transformado e inmediatamente después el operador que llevará a cabo la transformación) esto se representa con la siguiente ecuación:
A = ΛA’
Obsérvese que para representar al operador matricial propio de las transformaciones de Lorentz estamos utilizando la letra griega lambda (Λ) cuyo equivalente latino es la letra L.
Tomando en cuenta la forma en la cual se lleva a cabo la multiplicación de dos matrices A y B (cada elemento en el renglón i y en la columna j de la matriz resultante C se puede obtener de la suma de los productos apareados respectivos de los elementos de la matriz A del lado izquierdo a los cuales apunta horizontalmente el dedo índice de la mano izquierda en el renglón i por los elementos de la matriz B del lado derecho a los cuales apunta verticalmente el dedo índice de la mano derecha en la columna j):
determinamos de inmediato que las operaciones matriciales de transformación, representando a los vectores A y A’ como vectores columna, están indicadas por la siguiente ecuación matricial:
Con un simple intercambio en el orden de los renglones y en la posición de unas variables en las ecuaciones de transformación de Lorentz:
____x = γx’ + + γ(V/c) ct’ + 0y’ + 0z’
____ct = γ(V/c) x’ + γct’ + 0cy’ + 0cz’
____y = 0γx’ + 0(V/c) ct’ + 1y’ + 0z’
____z = 0γx’ + 0(V/c) ct’ + 0y’ + 1z’
podemos obtener la siguiente ecuación matricial que es un poco más reveladora:
Tenemos, en efecto, una submatriz, resaltada con fondo color amarillo, la cual transforma las coordenadas (x’, ct’) a las coordenadas (x, ct) dejando intactas a las coordenadas del eje-y y del eje-z en virtud de que entre los sistemas de referencia S’ y S no hay un movimiento relativo en los ejes-y y en los ejes-z, el único movimiento es en el eje-x. Entresacando dicha submatriz de la matriz general, obtenemos la matriz que verdaderamente proporciona la transformación en el eje-x, una transformación conocida como un boost (empuje) en la dirección del eje-x:
No se requiere de mucha imaginación para darse cuenta de que en caso de que el marco de referencia móvil S se esté moviendo a lo largo del eje-y en lugar de moverse a lo largo del eje-x, las ecuaciones de transformación serán:
____x = 1x’ + 0y’ + 0z’ + 0ct’
____y = 0x’ + γy’ + + 0z’ + γ(V/c) ct’
____z = 0x’ + 0y’ + 1z’ + 0ct’
____ct = 0x’ +γ(V/c) y’ + 0z’ + γct’
La representación matricial de este sistema de ecuaciones lineares es la siguiente:
Y cuando el movimiento relativo entre ambos marcos de referencia se esté dando en el eje-z, las ecuaciones de transformación serán:
____x = 1x’ + 0y’ + 0z’ + 0ct’
____y = 0x’ + 1y’ + 0z’ + 0ct’
____z = 0x’ + 0y’ + γz’ + γ(V/c) ct’
____ct = 0x’ + 0y’+ γ(V/c) z’ + γct’
La representación matricial de este sistema de ecuaciones lineares es la siguiente:
Obsérvese que, en cada caso, podemos entresacar una submatriz, la cual será siempre la misma cuando el movimiento ocurre a velocidad V a lo largo de solo uno de los ejes coordenados. Esta matriz es conocida como la matriz simple de Lorentz.
Utilizando el símbolo β definido como β = V/c, obtenemos una representación más compacta de la matriz simple de Lorentz:
Por razones de conveniencia que pronto serán obvias, haremos el cambio notacional a = γ y b = βγ, con lo cual nuestra matriz de Lorentz adquiere el siguiente aspecto:
Consideremos ahora las ecuaciones de la transformación inversa de Lorentz, utilizadas para efectuar el cambio de las coordenadas (x, y, z, ct) del marco de referencia S a las coordenadas (x’, y’, z’, ct’) del marco de referencia S’:
____x’ = γ(x - Vt)
____y’ = y
____z’ = z
____t’ = γ(t - Vx/c²)
Para poder obtener la submatriz que nos interesa, podemos ignorar las dos transformaciones intermedias que en realidad son transformaciones triviales, concentrándonos únicamente sobre las transformaciones que realmente nos interesan:
____x’ = γx - γ(V/c) ct
____ct’ = - γ(V/c) x + γct
No cuesta trabajo darse cuenta de que para la transformación inversa la submatriz será:
En notación matricial compacta, si A = [x, ct] entonces para obtener A’ = [x’, ct’] la operación matricial estará representada por la siguiente ecuación;
A’ = ΛA
Puesto que Λ es la transformación matricial que usamos para convertir las coordenadas del sistema de referencia S al sistema de referencia S’, y Λ es la transformación matricial que usamos para convertir las coordenadas del sistema de referencia S’ al sistema de referencia S, si aplicamos a un vector A primero la operación Λ y después la operación Λ debemos obtener el mismo vector A con el que habíamos comenzado originalmente:
ΛΛA’ = Λ (ΛA’) = Λ A = A’
(ΛΛ) A’ = A’
(ΛΛ) A’ = A’
Esto solo puede ser cierto si el producto matricial ΛΛ es igual a la matriz identidad I:
Se recuerda, por si se ha olvidado, o se informa, por si no se sabe, que por lo general la multiplicación de dos matrices no es una operación conmutativa, el orden de los factores sí altera el producto. El producto de dos matrices Q1 y Q2, tomado en el orden Q1Q2, producirá una matriz diferente a la que producen las mismas matrices tomadas en el orden Q2Q1:
Cuando son conmutativas, el producto de ambas resulta ser la matriz identidad I, ya que una de las matrices es la inversa de la otra.)
Todo lo anterior nos conduce a concluír que Λ tiene que ser la matriz inversa de la matriz Λ, lo cual representamos notacionalmente como Λ = Λ-1. Siendo así, entonces se debe cumplir la condición ΛΛ = I:
Llevando a cabo la multiplicación matricial del lado izquierdo de la igualdad e igualando componente a componente con la matriz del lado derecho, además de obtener la obvia condición trivial ab = ba obtenemos otra condición que no es trivial:
a² - b² = 1
Esto nos permite definir, formalmente y de modo riguroso, a una matriz simple de Lorentz como toda aquella matriz que tenga el aspecto
o el aspecto
para la cual se cumpla la condición
a² - b² = 1
El interés que podamos tener en las propiedades de las representaciones matriciales de las transformaciones de Lorentz va más allá de la afición que pueda haber en nosotros hacia las curiosidades de las matemáticas. Las transformaciones de Lorentz tienen un aspecto casi único, distintivo, característico de lo que llamamos un espacio-tiempo plano propio de la Teoría Especial de la Relatividad. Eventualmente llegará el momento de dar el salto hacia marcos de referencia no-inerciales, acelerados, en los cuales el espacio-tiempo no es plano sino que adquiere una curvatura. Y las matrices de transformación volverán a aparecer nuevamente pero bajo un aspecto más elaborado, propio de la Teoría General de la Relatividad. Pero tales matrices características de un espacio-tiempo curvo se reducen a las matrices características de las transformaciones de Lorentz cuando el marco de referencia acelerado que corresponde a los campos gravitacionales se puede considerar en una región pequeña del espacio como Lorentziano.
Existe otra forma de representar lo mismo que lo que representan las matrices cuadradas (rectangulares, de orden 2) en cuatro dimensiones, renombrando a las cuatro coordenadas bajo un esquema conocido como coordenadas generalizadas (x1, x2, x3, x4) y prescindiendo de matrices usando en lugar de ello sumatorias y dobles sumatorias, pero esto quedará postpuesto para cuando se lleve a cabo una discusión sobre el cálculo tensorial. De antemano se señala aquí que ambas formas de representación son completamente equivalentes, están representando lo mismo, y cada una de ellas tiene sus propias ventajas.
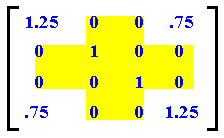
PROBLEMA: Determinar si la siguiente matriz
es una matriz de Lorentz.
Extraemos primero la submatriz que nos interesa tachando los renglones y las columnas que contienen únicamente unos y ceros:
La matriz de interés es la siguiente:
Haciendo a = 1.25 y b = .75, la matriz dada ciertamente tiene la configuración de una matriz Lorentziana. Sin embargo, falta ver si se cumple la condición principal:
a² - b² = (1.25)² - (.75)² = 1.5625 - 0.5625
a² - b² = 1
a² - b² = 1
Se concluye que la matriz es Lorentziana, y en los lugares en donde esta matriz aplica se cumplirán los postulados de la Teoría Especial de la Relatividad.
Al tratar el tema de las transformaciones de Lorentz, para derivar dichas ecuaciones de transformación se supuso, como se ha hecho desde un principio, que el movimiento relativo entre los dos marcos de referencia usuales S y S’ se lleva a cabo con uno de los marcos moviéndose a una velocidad constante V a lo largo del eje-x. Esto se hace con fines de simplificación. Los marcos de referencia pueden estarse moviendo el uno con respecto al otro en tal forma que no sólo haya un movimiento relativo entre ambos marcos a lo largo del eje-x, sino también que haya un movimiento relativo entre ambos a lo largo del eje-y e inclusive a lo largo del eje-z. De este modo, podríamos hablar de tres componentes de velocidad, Vx, Vy y Vz en lugar de una sola. En la situación clásica en donde utilizamos las transformaciones de Galileo, esto no presenta problema alguno porque allí las componentes de velocidad a lo largo de cada eje son independientes la una de la otra por completo. De este modo, si las transformaciones clásicas de un marco de referencia a otro cuando el movimiento relativo entre ambos marcos ocurre sólo a lo largo del eje-x son:
x = x’ + Vt’
y = y’
z = z’
y = y’
z = z’
entonces cuando el movimiento relativo entre ambos marcos ocurre a lo largo de los tres ejes las transformaciones de Galileo serán simplemente:
x = x’ + Vx t’
y = y’ + Vy t’
z = z’ + Vz t’
y = y’ + Vy t’
z = z’ + Vz t’
Desafortunadamente, en el caso de la Teoría Especial de la Relatividad, el asunto de ampliar la cobertura cuando el movimiento relativo entre ambos marcos ocurre a lo largo de los tres ejes en lugar de uno solo no es un asunto tan sencillo en virtud del requerimiento estricto del segundo postulado de la Teoría Especial de la Relatividad que nos dice que la velocidad de la luz medida por observadores situados en ambos marcos debe seguir siendo exactamente la misma. De este modo un rayo de luz, que tendrá tres componentes de velocidad proyectados sobre cada uno de los ejes en ambos marcos de referencia, debe tener el mismo valor constante por dondequiera que se le mire. La transformación general de Lorentz para esta situación, recurriendo a la ayuda de matrices con el fin de simplificar la notación, es la siguiente (se recomienda ampliar la imagen para poder leer mejor la ecuación matricial):
Como es de esperarse, la obtención de la transformación general de Lorentz es un asunto laborioso al que sólo se recurre cuando algún maestro que disfruta de su fama de “cruel” lo deja como tarea a sus alumnos (algo así como el draconiano Profesor Charles W. Kingsfield que aparece en la película The Paper Chase, protagonizado por John Houseman). El lector no deberá tener dificultad alguna en verificar la transformación general de Lorentz que se ha dado arriba tomando en cuenta que la designación de las coordenadas es un asunto arbitrario, haciendo por ejemplo βy = βz = 0 con lo cual se debe obtener como caso especial la transformación de Lorentz cuando el movimiento relativo ocurre únicamente a lo largo del eje-x, tras lo cual se puede hacer βx = βz = 0 para comprobar el segundo caso (movimiento relativo a lo largo del eje-y), y finalmente βx = βy = 0 (movimiento relativo a lo largo del eje-z).
En realidad, si estamos realmente interesados en derivar las relaciones que corresponden a la transformación general de Lorentz cuando los marcos de referencia están en movimiento relativo el uno con respecto al otro a través de tres ejes coordenados en lugar de uno solo, la demostración se puede simplificar enormemente si recurrimos a notación vectorial clásica denotando como el vector posición x a la ubicación de un punto en el sistema coordenado S:
x = (x, y, z)
y denotando la ubicación del mismo punto en el sistema coordenado S’ como:
x’ = (x’, y’, z’)
simbolizando asimismo a la velocidad relativa V que hay entre los dos marcos de referencia como un vector V (con letra negrita) con componentes relativos en cada uno de los tres ejes Cartesianos:
V = (Vx, Vy, Vz)
Lo anterior lo hacemos en conjunción con la notación vectorial del producto punto ó producto escalar entre dos vectores:
x · V = (x, y, z) · (Vx, Vy, Vz) = xVx + yVy + zVz
Con esta notación, la transformación general de Lorentz que estamos buscando tanto para las componentes espaciales como para la componente temporal se puede resumir vectorialmente en las siguientes dos fórmulas:
Resta decir que para la derivación de estas dos fórmulas debemos aferrarnos estrictamente de principio a fin al manejo matemático vectorial que se acostumbra darle a los problemas típicos de la mecánica clásica en los que se manejan cantidades vectoriales.
Habiendo visto una representación matricial para la transformación generalizada de Lorentz, no debe causarnos ningún asombro el hecho de que la siguiente matriz también sea una matriz de Lorentz:
Esto nos debe dejar en claro cuál es la diferencia entre una matriz simple de Lorentz como las que vimos arriba, y una matriz de Lorentz ordinaria.
Determinar si una matriz 4x4 como la de arriba es una matriz de Lorentz no es un asunto complicado. Ello requiere derivar primero tres relaciones generales a partir de lo que vendría siendo la invariancia de la ecuación del cono de luz (en referencia a los diagramas de Minkowski). Pero para ello tenemos que tener en claro cuál es esa invariancia a la que nos estamos refiriendo, razón por la cual este asunto debe quedar postpuesto hasta que no haya sido desarrollado dicho tema.
La multiplicación de dos matrices A y B tiene desde luego una definición más formal que la definición intuitiva que se ha dado arriba, y es la siguiente:
Este enunciado nos dice que para dos matrices A = (apq) y B = (brs), siendo A una matriz de p renglones y q columnas, y siendo B una matriz de r renglones y s columnas, el producto de las mismas definido en el orden AB es tal que cada elemento cij de la matriz resultante deberá ser obtenido de acuerdo a la relación anterior, para lo cual es requisito indispensable que el número de columnas de la matriz A sea igual al número de renglones de la matriz B, o sea q = r.
En la definición formal que se acaba de dar para el producto de dos matrices, obsérvese un detalle interesante: la sumación se lleva a cabo sobre el sub-índice que está repetido, en este caso k. Si alguien borrara el símbolo Σ de la sumatoria en la expresión de arriba, no tendríamos dificultad alguna para reestablecerlo junto con el índice que fue borrado. Tan sólo tendríamos que fijarnos en el sub-índice que aparece repetido.
PROBLEMA: Escribir la expresión para evaluar el elemento c47 resultante del producto AB de dos matrices A y B si la matriz A es una matriz de cinco renglones y nueve columnas (representado como 5x9), y la matriz B es una matriz de nueve renglones y ocho columnas (representado como 9x8).
En este caso, el producto matricial está definido, puesto que el número de columnas de la matriz A es igual al número de renglones de la matriz B, o sea:
[5x9] [9x8]
Podemos ver también aquí que la sumatoria deberá correr desde n =1 hasta n = 9 y que la matriz resultante será una matriz 5x8.
Utilizando la definición formal dada arriba, el elemento c47 estará dado por la siguiente sumatoria:
c47 = ______________________________________
a41b17 + a42b27 + a43b37 + a44b47 + a45b57 + a46b67 + a47b77
a41b17 + a42b27 + a43b37 + a44b47 + a45b57 + a46b67 + a47b77
PROBLEMA: Si postmultiplicamos una matriz A cuyo tamaño es 5x4 por una matriz B cuyo tamaño es 4x7, y el producto resultante los postmultiplicamos por otra matriz C cuyo tamaño es 7x3, ¿cuál será el tamaño de la matriz resultante?
[5x4][4x7][7x3]
Podemos ver que la matriz resultante será una matriz 5x3.
PROBLEMA: La siguiente cantidad
cΔt² - x² - y² - z²
resulta ser de gran utilidad en el análisis de problemas propios de la Teoría Especial de la Relatividad. Representar dicha cantidad en forma matricial.
Formando un vector renglón [ cΔt, x, y, z ] y tomando la transpuesta del mismo para formar el vector columna correspondiente, la cantidad
cΔt² + x² + y² + z²
quedaría representada matricialmente por el siguiente producto matricial entre una matriz que consta de un renglón y cuatro columnas (1x4) y una matriz que consta de una columna y cuatro renglones (4x1):
Pero queremos además la selección de signos que se nos han indicado. Esto se logra injertando entre las dos matrices de arriba una matriz intermedia:
En notación matricial más compacta y haciendo X = [ cΔt, x, y, z ], lo anterior se puede escribir como XAXT en donde A es la matriz intermedia y XT es la transpuesta de la matriz X. Llevando a cabo el producto matricial ya sea en el orden (XA)XT multiplicando primero las dos matrices de la izquierda y multiplicando la matriz resultante por la matriz a la derecha, o en el orden X(AXT) multiplicando primero las dos matrices de la derecha y multiplicando la matriz resultante por la matriz de la izquierda, podemos ver que esta representación matricial nos produce la expresión deseada.
La matriz intermedia A del problema representa los 16 componentes de un objeto que se conoce como el tensor métrico de un espacio-tiempo plano (Lorentziano), el cual se representa en forma abreviada ya sea como g = (gij) usando sub-índices o como g = (gij) usando super-índices. El concepto del tensor métrico es generalizado hacia un espacio-tiempo curvo en la Teoría General de la Relatividad.
Llevaremos ahora a cabo la post-multiplicación de un vector renglón U de tres elementos:
por una matriz cuadrada g de tamaño 3x3:
post-multiplicado todo por un vector columna V de tres elementos:
Procedemos a formar el producto matricial UgV de la manera siguiente:
Llevaremos a cabo la multiplicación de estas tres cantidades multiplicando primero la segunda por la tercera siguiendo la regla para la multiplicación de matrices dada arriba:
El resultado final de la operación UgV resulta ser una sola cantidad, la cual viene siendo evaluada a fin de cuentas de la siguiente manera:
UgV =_______________
a1 g11 b1 + a1 g12 b2 + a1 g13 b3
+ a2 g21 b1 + a2 g22 b2 + a2 g23 b3
+ a3 g31 b1 + a3 g32 b2 + a3 g33 b3
a1 g11 b1 + a1 g12 b2 + a1 g13 b3
+ a2 g21 b1 + a2 g22 b2 + a2 g23 b3
+ a3 g31 b1 + a3 g32 b2 + a3 g33 b3
La evaluación de esta cantidad la podemos obtener sin ayuda de representaciones gráficas con la ayuda de dos sumatorias:
No cuesta mucho trabajo convencerse de que, si llevamos a cabo las dos sumaciones, obtendremos el resultado final del producto triple UgV. No importa que se lleve a cabo primero la sumación sobre p y después la sumación sobre q, o bien primero la sumación sobre q y luego la sumación sobre p, porque es cosa fácil de comprobar el hecho de que en una sumatoria múltiple el orden en que se llevan a cabo las sumaciones no altera el resultado final.
Al llevar a cabo el producto UgV, empezamos con dos vectores y una matriz, y terminamos al final con un solo número. ¿Significa esto que hubo una metamorfosis en la cual terminaron perdiéndose los paréntesis cuadrados? Bueno, no precisamente. Podemos ver simbólicamente que el resultado de estos productos será una matriz 1x1:
En pocas palabras, para la matriz UgV el resultado final será:
[1x3][3x3][3x1] = [1x1]
De este modo, el número solitario que llamamos escalar en realidad sigue siendo una matriz, una matriz que consta de un solo renglón y una sola columna, una matriz de tamaño 1x1 que consta de un solo elemento, pero al fin y al cabo una matriz. Naturalmente, si este elemento representa una temperatura o una frecuencia, prescindimos de la formalidad simbólica y utilizamos a dicho elemento en cálculos posteriores como si fuese un número cualesquiera. Pero no hay que olvidar que, formalmente, todas las operaciones llevadas a cabo con vectores y matrices siempre terminan produciendo otros vectores y matrices.
Ahora bien, vamos a considerar al vector renglón U como lo que verdaderamente es, una matriz que consta de un renglón y tres columnas, o sea, una matriz 1x3. En tal caso, podemos formalizar la representación de cada elemento agregando un 1 a cada sub-índice, de modo tal que el elemento a11 es el elemento que corresponde al primer (y único) renglón en la primera columna de la matriz, el elemento a12 es el elemento que corresponde al primer renglón en la segunda columna de la matriz, y el elemento a13 es el elemento que corresponde al primer renglón en la tercera columna de la matriz:
Haremos también algo similar con el vector columna V, lo vamos a considerar como lo que verdaderamente es, una matriz que consta de tres renglones y una columna, o sea, una matriz 3x1. En tal caso, podemos formalizar la representación de cada elemento poniendo un 1 después de cada cada sub-índice, de modo tal que el elemento b11 es el elemento que corresponde al primer renglón en la primera (y única) columna de la matriz, el elemento b21 es el elemento que corresponde al segundo renglón en la primera columna de la matriz, y el elemento b31 es el elemento que corresponde al tercer renglón en la primera columna de la matriz:
Con este ligero cambio notacional, el producto UgV se escribe en notación matricial de la siguiente manera:
La representación del producto matricial triple mediante una doble sumatoria será entonces:
Un momento de reflexión nos revela que si en lugar del vector U de tamaño 1x3 tenemos una matriz de tamaño ix3, y que si en lugar del vector V de tamaño 3x1 tenemos una matriz de tamaño 3xj, entonces el resultado final del producto de las tres matrices será una matriz M = (mij) de tamaño ixj, y para calcular el valor de cada elemento mij de dicha matriz todo lo que tenemos que hacer en la doble sumatoria de arriba es reemplazar el primer sub-índice 1 en la variable a por i, y reemplazar el segundo sub-índice 1 en la variable b por j, obteniendo la siguiente relación:
Lo que se acaba de hacer aquí es la obtención de la definición formal del producto de tres matrices. Obsérvese que en los límites superiores de las sumatorias para esta definición que acabamos de obtener el tamaño intermedio ya no está limitado hasta p = q = 3, podemos utilizar matrices del tamaño que queramos siempre y cuando dichos tamaños estén en concordancia con la definición de compatibilidad que se ha dado para productos matriciales (no podemos multiplicar una matriz 4x3 por una matriz 2x5 en ningún orden).
Obsérvese también otro detalle interesante. Si alguien borrara los símbolos Σ de las sumatorias en la expresión de arriba, no tendríamos dificultad alguna en reestablecerlos. Tan sólo tendríamos que fijarnos en los sub-índices que están repetidos. De este modo, si lo que vemos escrito es lo siguiente:
aip gpq bqj
entonces con tan sólo mirar los sub-índices que están repetidos (en este caso los sub-índices p y q) podemos volver a poner las sumatorias en el orden que queramos (que al fin y al cabo el orden en el cual se lleven a cabo las sumaciones no altera el resultado final de la sumación). Esto será de utilidad posteriormente cuando entremos en el estudio del análisis tensorial que a su vez es requerido para formular los principios y resolver los problemas que corresponden a la Teoría General de la Relatividad. Mientras tanto, en base a lo que acabamos de ver, podemos hacer unívocamente la siguiente afirmación sin temor a equivocarnos:
El resultado final de todo producto matricial múltiple (involucrando dos o más matrices) puede ser representado no sólo gráficamente mediante matrices sino también con la definición formal basada en el uso de las sumatorias.
De este modo, contamos ya con dos representaciones distintas para la misma cosa.
Tomando en cuenta que el producto de dos matrices no es una operación conmutativa salvo en casos especiales, esta es una buena ocasión para señalar que para que una sumatoria múltiple pueda ser representada en forma alterna como el producto de varias matrices cuando tal cosa sea posible, ayuda mucho el acomodar los factores de la sumatoria de modo tal que la conversión a la representación matricial se pueda llevar a cabo directamente. A modo de ejemplo, en la siguiente sumatoria múltiple:
no resulta nada claro cuál podría ser la representación matricial correspondiente. Pero si reacomodamos los factores de la sumatoria de la siguiente manera usando como guía el requerimiento de que los sub-índices tienen que estar apareados conforme son leídos de izquierda a derecha en la sumatoria ya transformada:
la representación matricial salta a la vista casi de inmediato, la cual en notación matricial compacta resulta ser:
XTΛT G Λ X
Obsérvese cuidadosamente que para poder lograr esta representación matricial, tomando en cuenta que la sumatoria múltiple debe producir al final un número (que matricialmente viene siendo una matriz que consta de un solo renglón y de una sola columna, algo que tenemos que saber de antemano para evitarnos mucho trabajo), la necesidad de aparear los sub-índices nos obligó a tomar la transpuesta de la matriz Λ, la cual representamos de color rojo como ΛT; y también nos obligó a usar la representación del vector columna X como el vector renglón tomando la transpuesta de X y representándolo como XT. Esto significa que en la sumatoria múltiple preparada para su representación matricial en donde aparecen XT y ΛT de color rojo como corresponde a las transpuestas, si bien en lo que respecta al componente xi dentro de la sumatoria el cambio no tiene efecto alguno, el componente λir en caso de llevarse a cabo la sumación sobre esa expresión tiene que ser interpretado no como el elemento dentro de la matriz Λ que está en el renglón i y la columna r sino como el elemento dentro de la matriz que está dentro del renglón r y la columna i.