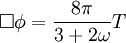Para resolver y estudiar esta cuestión, Einstein formuló un principio sobre el cual descansa toda la Teoría General de la Relatividad a la cual nos podemos referir simplemente como la Relatividad General: el principio de equivalencia, el cual nos dice lo siguiente:
Principio de Equivalencia: Para una persona situada dentro de una caja herméticamente sellada, no existe diferencia entre el estar en el espacio con la caja acelerándose y otra persona situada en una caja similar reposando en un campo gravitacional.
Puesto de otra manera, si la persona está encerrada en una caja blindada del exterior, la persona no tiene forma alguna de saber si la caja está en el espacio acelerándose o si la caja está en presencia de un campo gravitacional. Ambas condiciones son equivalentes para cualquier tipo de experimento que pretenda llevar a cabo. Esto lo podemos ilustrar de la siguiente manera:
En el dibujo de la izquierda, tenemos a un astronauta cuya nave espacial está acelerándose hacia arriba. Si el astronauta suelta una pelota, la pelota caerá hacia abajo como consecuencia de la aceleración. Y en el dibujo de la derecha, tenemos a una persona cuya caja en la que se encuentra está en reposo en un campo gravitacional. También esta persona, si suelta una pelota, la verá caer hacia abajo pero esta vez como consecuenciade la atracción ejercida por el campo gravitacional. Ambas personas ven caer la pelota hacia abajo. Y si la caja en la que están encerradas es una caja herméticamente sellada y blindada, no tienen forma de saber en base a cualquier experimento que pretendan llevar a cabo si están en una caja que se está acelerando en el espacio o si están en una caja que está en reposo en un campo gravitacional.
En el experimento hipotético considerado en la entrada “El germen de una idea” con nuestro proverbial viajero montado en un carrousel que va pasando a velocidades cada vez mayores frente a dos esferas metálicas que a causa de la contracción de longitud relativista propia de la Teoría Especial de la Relatividad parecen irse acercando la una a la otra como si hubiese una fuerza de atracción mágica entre ellas, la objeción podría formularse de que al pasar frente a las esferas metálicas el viajero está experimentando una aceleración lineal, constante, y lo que vería serían las esferas metálicas acercándose la una a la otra a una velocidad constante, no a una aceleración constante propia de una atracción gravitacional. Pero se recuerda aquí que la aceleración producida por la gravedad de la Tierra en su superficie (de 9.8 metros/segundo²) es válida únicamente en la superficie de la Tierra. A distancias cada vez mayores de nuestro planeta esa aceleración va disminuyendo hasta tomar prácticamente un valor de cero, de modo tal que esta aceleración gravitacional no es constante. Del mismo modo, si la aceleración que experimenta el viajero cada vez que pasa frente a las esferas metálicas no es constante sino que va aumentando en forma graduada, el viajero verá a las esferas metálicas “atraerse” en forma acelerada, propia de un campo gravitacional. Y esto justifica ya la equivalencia de un campo gravitacional como consecuencia directa de efectos relativistas.
Detrás del Principio de Equivalencia subyace algo que inclusive el mismo Newton había ya sospechado y considerado en su época, la equivalencia entre la masa inercial y la masa gravitacional de un cuerpo. La masa inercial es esencialmente la resistencia que presenta un cuerpo flotando en el espacio a ser acelerado, precisamente es a lo que se refiere la ley de la inercia de Newton cuando nos dice que todo cuerpo de masa m presenta una resistencia a que se le cambie su cantidad de movimiento, resistencia al cambio ocasionada precisamente por su masa inercial mi. Por otro lado la masa gravitacional es la atracción que ejerce un campo gravitacional sobre un cuerpo que medida nos indicaría una masa mg para dicho cuerpo. La masa inercial es la que posee un cuerpo que está flotando en el espacio vacío interestelar, es la característica propia del cuerpo que se resiste a ser acelerado sacándolo de su estado inerte o estado de reposo poniéndolo en movimiento (regresándolo “a la vida”) cuando se le aplica una fuerza, mientras que la masa gravitacional es la que determina el peso de un cuerpo en reposo descansando sobre la superficie de un planeta, es la que determina que una persona sea más ligera sobre la superficie de la Luna que sobre la superficie de la Tierra, y más pesada sobre la superficie de Saturno. Clásicamente, en el espacio vacío, la fuerza F requerida para provocar una aceleración a sobre un cuerpo está dada por la fórmula:
F = mi a
mientras que sobre la superficie de la Tierra el peso W de un cuerpo está dado por una fórmula semejante:
W = mg g
siendo g la aceleración que tendría un cuerpo al ser dejado caer en la superficie de la Tierra.
La masa inercial es una medida de la resistencia de una masa al cambio de velocidad, mientras que la masa gravitacional es la medida de la fuerza de atracción gravitatoria que experimenta una masa en relación a la demás de acuerdo con la fórmula Newtoniana para la fuerza gravitatoria entre dos partículas. Einstein lo que hizo fué, en efecto, adoptar matemáticamente la relación:
mi = mg
elevándola al grado de postulado básico para usarla como punto de partida para su Teoría General de la Relatividad.
Es importante aclarar que no hay razón a priori para suponer que la masa inercial de un cuerpo sea igual a su masa gravitacional del mismo modo que no hay razón a priori para suponer que un kilogramo de masa gravitacional de un bloque metálico de hierro tenga las mismas propiedades físicas que la masa gravitacional de un bloque metálico de níquel (independiente del tipo de elemento del que está formado el bloque), y del mismo modo que no hay razón alguna para suponer de antemano que la cantidad de átomos que contenga un gramo de azúcar sea igual a la cantidad de átomos que contenga un gramo de agua. Este tipo de datos son información que se recaba experimentalmente, de la experiencia. Hasta donde nos lo han permitido numerosos experimentos efectuados con un grado de precisión muy alto, la masa inercial y la masa gravitacional se pueden tomar como si fueran iguales; si no lo son posiblemente no exista en la actualidad un experimento con la suficiente sensibilidad que nos permita detectar esa mínima diferencia que pudiera haber entre ambas (por ejemplo, de una parte en 1080, lo cual estaría fuera de nuestro alcance).
El principio de equivalencia nos permite partir de la base que ya tenemos, la Teoría Especial de la Relatividad, en donde se ha supuesto que el espacio-tiempo es plano, considerando fenómenos de aceleración dentro de dicha teoría y dando por hecho que, si la aceleración es la misma, el comportamiento de un cuerpo será el mismo ya sea que esté siendo acelerado en el espacio libre mediante la aplicación de una fuerza (masa inercial) o que se encuentre en estado de reposo en un campo gravitacional que le pueda provocar la misma aceleración si se le deja caer (masa gravitacional). El efecto de las aceleraciones es incorporado dentro del modelo matemático de la Teoría de la Relatividad dejando atrás el modelo plano del espacio cuatri-dimensional propio de la Teoría Especial de la Relatividad, para permitirle al plano tomar una curvatura. En efecto, el continuum tiempo-espacio puede adquirir una curvatura. ¿Y qué es lo que puede provocar tal curvatura en un modelo plano en el que únicamente aplicaban los principios de la Teoría Especial de la Relatividad? La presencia de masa. En donde hay alguna masa, el espacio-tiempo resiente una deformación, la cual será mayor tanto mayor sea la masa que está produciendo la curvatura. La imagen típica con la cual se intenta transmitir esta idea es la de una malla flexible con la cual se intenta simbolizar un espacio-tiempo plano de Minkowski, sobre la cual se coloca una esferita metálica que provoca el hundimiento que nos representa la curvatura:
Sin embargo, es importante no tomar muy a pecho esta representación pictórica de la curvatura introducida en un espacio-tiempo plano por la presencia de una masa, en virtud de que lo que se está tratando de representar es una curvatura que ocurre en cuatro-dimensiones, utililizando para ello no una representación gráfica cuatri-dimensional, ni siquiera una representación tri-dimensional, sino una representación plana como la que tenemos arriba. La imagen sirve únicamente para los fines de transmitir una idea, la idea de una curvatura en el espacio-tiempo plano, pero no tiene intención alguna de ser interpretada literalmente.
Como en base a uno de los resultados básicos de la Teoría Especial de la Relatividad, la masa y la energía son equivalentes, ambas son manifestaciones diferentes de la misma cosa, pudiendo referirnos a ambas como la masa-energía, dentro de la Relatividad General podemos afirmar que toda presencia de masa-energía introduce una curvatura en el continuum espacio-tiempo. En donde no hay masa-energía (en castellano, en donde no hay nada de masa ni de energía) cercana no habrá tampoco ninguna curvatura en el espacio-tiempo, y las fórmulas propias de la Teoría Especial de la Relatividad son las únicas que necesitamos para estudiar los fenómenos que se presenten en dicha región. Expresado sin recurrir a fórmula alguna:
curvatura = concentración de masa y energía
Esto es simbolizado de manera más formal con la ecuación más importante de la Teoría General de la Relatividad:
Esta es la ecuación dimensionalmente correcta. Sin embargo, al igual que como ocurre en la Teoría Especial de la Relatividad para fines de análisis y para fines de representación esquemática en los diagramas espacio-tiempo de Minkowski, dada la enorme magnitud de la cifra que representa la velocidad de la luz se acostumbra por convención hacerla igual a la unidad, o sea c = 1, con lo cual tenemos a la ecuación en una de sus representaciones más populares:
En el lado izquierdo de la ecuación tenemos una entidad conocida como la curvatura, representada por el símbolo G. Y del lado derecho tenemos tenemos otra entidad que representa todo lo que tiene que ver con la masa-energía, absolutamente todo, simbolizada como T. La constante G es la constante de gravitación universal que en el sistema de mediciones métrico decimal es igual a 6.674215 x 10-11 m3/kg-seg², una constante que debe ser medida y obtenida experimentalmente; se trata de la misma constante universal que Newton requirió usar para que su fórmula de atracción gravitacional entre dos cuerpos concordase con los fenómenos astronómicos analizados bajo la mecánica Newtoniana. Puesto que 8 y π son también constantes (numéricas) el factor 8πG en sí no es más que una constante, de la cual si prescindimos tenemos una relación cualitativa que del lado derecho nos está simbolizando la curvatura en el espacio-tiempo y del lado derecho nos está simbolizando el contenido en masa-energía y momentum que está produciendo la curvatura señalada. Debe enfatizarse el hecho de que la curvatura en la carta (manifold) espacio-tiempo es una curvatura de un espacio en cuatro dimensiones, y por lo tanto no es una curvatura que podamos percibir geométricamente de manera directa. Esta curvatura la percibimos a través de los efectos que produce tales como la rotación de los planetas alrededor del Sol. La curvatura en el espacio-tiempo le dice a la masa-energía cómo y en qué sentido debe moverse, mientras que la masa-energía le dice al espacio-tiempo cuánto y de qué manera debe “curvearse”. Esta ecuación lo que nos está diciendo esencialmente es que cuando T no tiene un valor de cero (en todas sus componentes), G tampoco lo tendrá (en todas sus componentes) y por lo tanto habrá una curvatura en el continuum tiempo-espacio. El lector avispado tal vez empiece a percibir aquí un problema: si A le dice a B cómo debe moverse, y si B le dice a A cómo debe “curvearse” para que B a su vez le diga a A cómo debe moverse, ¿entonces cómo vamos a resolver las ecuaciones que nos describan cualquier tipo de situación? Es aquí que tenemos que confrontar una dura realidad: los problemas postulados dentro del marco de la Teoría General de la Relatividad, hablando en términos generales, son irresolubles matemáticamente, sólo se pueden obtener soluciones exactas para casos particulares o recurriendo a aproximaciones. Afortunadamente, hay algunos casos particulares, especialmente aquellos en los que tomamos ventaja de la simetría esférica, en donde podemos obtener soluciones exactas a las ecuaciones de Einstein. Pero el caso general, sobre todo el caso en el que tenemos que recurrir a simulaciones computarizadas a causa de la no-linearidad de las ecuaciones diferenciales involucradas, es algo que inclusive justifica el tener que recurrir a las supercomputadoras de hoy en día para poder encontrar soluciones razonablemente aproximadas.
Siguiendo una idea propuesta inicialmente por Max Planck de asignarle a las constantes físicas un valor unitario en vez de utilizar sistemas de medición concebidos artificialmente por el hombre que no están basados en algo válido en el Universo entero que sea independiente de criterios arbitrarios, en lo que Max Planck llamó “unidades naturales” y que en la Teoría de la Relatividad se conoce como unidades geometrizadas a la constante de gravitación universal G se le asigna también un valor de 1. Con esto, la ecuación más importante de la Teoría General de la Relatividad se nos presenta frecuentemente en muchos textos y trabajos científicos de la siguiente manera simplificada:
Hay que tener mucha precaución con esta que podemos considerar la fórmula fundamental de la Teoría General de la Relatividad, porque es una ecuación tensorial, y el nombre correcto de G es el de tensor de curvatura de Einstein, mientras que el nombre correcto de T es el de tensor energía-momentum ó tensor energía-tensión ó tensor energía-impulso, y cada uno de ellos requiere para su especificación completa un total de 16 componentes. Las ecuaciones del campo gravitacional o simplemente ecuaciones de campo de la Relatividad General, expresadas en su forma más explícita, tienen el siguiente aspecto en notación tensorial:
R - ½gR = 8πGT
en donde R = (Rμν) es el tensor de curvatura de Ricci, R es el escalar de Ricci, g = (gμν) es el tensor métrico y T = (Tμν) es el tensor energía-tensión o tensor energía-impulso (stress-energy tensor). En notación de sub-índices, la anterior ecuación se escribe de la siguiente manera:
En un espacio de cuatro dimensiones, cada uno de los tensores representa una cantidad física que consta de 16 componentes y la cual puede ser representada como una matriz 4x4. A manera de ejemplo, las 16 componentes del tensor T = (Tμν), expresadas en forma de matriz, tienen el siguiente aspecto:
En su formulación de la ecuación fundamental de la Teoría General de la Relatividad, Einstein siguió el ejemplo de Maxwell en su derivación de las cuatro ecuaciones básicas del electromagnetismo, para las cuales Maxwell utilizó notación vectorial con lo cual las fórmulas generales simplificadas se vuelven independientes del tipo de coordenadas (Cartesianas, polares, cilíndricas, esféricas, etc.) que se utilicen para describir algún fenómeno electromagnético en particular. Puesto que la formulación de la Teoría General de la Relatividad requiere de un espacio de cuatro dimensiones (cuatri-dimensional), el uso de vectores no es suficiente para la simplificación de todo hasta reducirlo a una fórmula (o a unas cuantas fórmulas), se requiere el uso de notación tensorial. Sin embargo, es importante señalar aquí que los vectores, esas magnitudes físicas que tienen dirección y sentido tales como la aceleración de un automóvil o la fuerza que se le aplica a una palanca, en realidad también son tensores, tensores de orden uno. Y de hecho, todas las demás magnitudes físicas conocidas como escalares, esas magnitudes físicas que no tienen dirección y sentido tales como la temperatura de un objeto, también son tensores, tensores de orden cero. Al estar hablando de tensores, debe ir quedando claro que tendremos que ir un paso más allá del cálculo infinitesimal ordinario que se enseña en los bachilleratos, tendremos que familiarizarnos con las técnicas del cálculo diferencial absoluto, hoy mejor conocido como el cálculo tensorial, inventado por el matemático italiano Gregorio Ricci y publicado por su alumno Tullio Levi-Civita en un libro que sigue siendo de actualidad hoy en día, The Absolute Differential Calculus.
La ecuación tensorial básica de la Relatividad General, expresada en función de coordenadas generalizadas (las cuales como ya se dijo pueden ser Cartesianas, polares, etc.) y escrita de la siguiente manera (usando subíndices):
Gμν = 8πGTμν
adquiere su forma más sencilla cuando en el espacio circundante no hay nada de masa ni energía presentes, en cuyo caso todos los componentes del tensor Tμν son iguales a cero, lo cual equivale a decir que el tensor T = (Tμν) es igual al tensor cero 0, o sea T = 0 lo que a su vez implica que G = 0. Para que el espacio-tiempo en alguna región del Universo sea plano, Lorentziano, propio de la Teoría Especial de la Relatividad, la condición fundamental es que el tensor de Einstein G sea igual al tensor cero.
Como ya se mencionó, el conjunto de ecuaciones representadas de esta manera (tensorial) es conocido como las ecuaciones de campo. Si utilizamos coordenadas Cartesianas (x1, x2 , x3), entonces como una de las coordenadas es la coordenada que corresponde a la variable tiempo t tanto la variable μ como la variable ν pueden representar a cualquiera de las cuatro coordenadas del espacio-tiempo (x1, x2 , x3 , t). Hasta aquí hemos estado utilizando coordenadas Cartesianas, rectangulares, pero podemos usar cualquier otro tipo de coordenadas adecuadas a nuestros propósitos. Si utilizamos coordenadas esféricas (r, θ, φ) para especificar la distancia radial, el ángulo del cenit θ y el ángulo azimutal φ, entonces en el espacio cuatri-dimensional (r, θ, φ, t) también tanto la variable μ como la variable ν pueden representar a cualquiera de las cuatro coordenadas en este espacio-tiempo especificado por estas coordenadas esféricas, de modo tal que varios valores típicos de Gμν y de Tμν vendrían siendo:
Grθ , Gθφ , Gφt
Ttθ , Trr , Tφθ
Ttθ , Trr , Tφθ
Es importante resaltar aquí que, por simetría Gμν= Gνμ, de modo tal que, por ejemplo:
Grθ = Gθr
Gφt = Gtφ
Gφt = Gtφ
Igualando los componentes respectivos de Gμν y Tμν en una ecuación tensorial para un caso particular, tenemos un sistema de ecuaciones con el cual en principio podemos resolver el problema matemáticamente, lo cual a primera vista parecería fácil. Desafortunadamente, las ecuaciones que involucran al tensor de curvatura de Einstein G son ecuaciones diferenciales, ecuaciones que involucran derivadas, así que el problema ya no es tan fácil. Peor aún, las ecuaciones diferenciales resultantes por lo general resultan ser ecuaciones diferenciales no-lineares, precisamente la situación matemática más difícil de todas. Para dar mayor detalle, la forma precisa de la curvatura del espacio-tiempo está determinada por un total de 12 ecuaciones del tipo que en matemáticas se conoce como ecuaciones diferenciales parciales hiperbólicas acopladas. Esto nos limita severamente la cantidad de problemas que pueden ser resueltos de manera exacta bajo algún sistema de coordenadas, llevándonos a considerar casos especiales como el caso en el que la masa de uno de un par de cuerpos es mucho mayor que la masa del otro cuerpo que tiene cerca. Aún así, hay triunfos espectaculares, como el logrado por Karl Schwarzschild, el cual en una solución matemática dada a las ecuaciones de campo de Einstein (una solución que impresionó a este último porque no creía factible la posibilidad de encontrar soluciones exactas a sus ecuaciones de campo) sentó las bases para la predicción de la existencia de los agujeros negros, regiones del espacio-tiempo con un campo gravitacional tan intenso que ni siquiera a la misma luz puede escapar.
El que el espacio-tiempo pueda ser objeto de una torsión (curvatura) causada por la cercanía de masa-energía tiene implicaciones directas tanto para el espacio medido por diferentes observadores como para el tiempo medido por diferentes observadores. En el caso del espacio, éste va experimentando una contracción relativista conforme un cuerpo se va acercando a un objeto de masa apreciable como la Tierra:
Del mismo modo, en el caso del tiempo, éste va experimentando una dilatación relativista conforme el cuerpo se va acercando a la Tierra:
El principio de equivalencia nos permite entender mejor algo que había quedado en cierta forma inconcluso y pendiente en una entrada previa titulada “Una teoría libre de asimetrías y de paradojas”, la paradoja de los gemelos. En dicha entrada se había señalado que la razón por la cual uno de los gemelos envejece más que el otro es porque existe una asimetría en la cual uno de los gemelos permanece en estado de reposo mientras que el otro que viaja en una nave espacial experimenta una aceleración para ponerse en marcha hacia la estrella (o el planeta) distante, experimenta otra aceleración para detenerse y dar la vuelta en sentido contrario (lo cual equivale a un cambio en los marcos de referencia) y experimenta otra aceleración para encaminarse de regreso hacia la Tierra. Como lo acabamos de ver, en un campo gravitacional el tiempo se dilata. Pero de acuerdo con el principio de equivalencia, desde el punto de vista relativista no existe diferencia alguna entre el estar en un campo gravitacional y el estar en un marco de referencia acelerado (ambos con la misma magnitud de aceleración). Entonces el tiempo medido por un viajero en una nave espacial que se está acelerando está dilatado igualmente que si se encontrara situado dentro de un campo gravitacional. Con ello, queda explicada cualitativamente la paradoja de los gemelos. Ponerle números al asunto requiere la formulación matemática precisa dada por Einstein, lo cual requiere acceder a las herramientas propias del cálculo tensorial.
A continuación tenemos una página del manuscrito escrito por Einstein dando forma a su Teoría General de la Relatividad:
En la misma publicación científica Annalen der Physik en donde en 1905 Einstein dió a conocer al mundo la Teoría Especial de la Relatividad, once años después se publicó en 1916 en Leipzig la primera introducción a la Relatividad General en el volumen 49 del Annalen der Physik, bajo el título “Die Grundlage der allgemeinen Relativitatstheorie”, un trabajo en la cual se avanzó por vez primera el concepto revolucionario de que la atracción de la gravedad es el resultado de una curvatura en el espacio-tiempo y no el resultado de una fuerza entre dos cuerpos como lo había propuesto Newton:
Por el interés histórico que pueda despertar en los estudiosos sobre el tema así como por la visión que nos puede dar sobre la manera en la cual Einstein fue dando forma matemática a su Teoría General de la Relatividad, se ha incluído como acompañante de esta obra un apéndice en el que se reproducen algunas de las páginas manuscritas del libro de apuntes (cuaderno de notas) de Einstein dentro del cual fue anotando las ideas conforme se iban desarrollando en su mente con el paso de los meses y los años, el cual ha sido puesto bajo el título “Relatividad General: Manuscritos originales”.
Como ya se señaló, el salto de un espacio-tiempo plano a un espacio-tiempo curvo requerirá de un uso intensivo no sólo de las herramientas del cálculo infinitesimal, requerirá del manejo de cuatro dimensiones a la vez mediante el cálculo infinitesimal extendido a las cuatro dimensiones, lo cual requerirá sistematizar las herramientas que ya teníamos dentro de otro conjunto de técnicas conocidas como el análisis tensorial o cálculo tensorial en el cual extendemos el concepto de magnitudes físicas como la temperatura y la masa sin dirección y sentido (escalares) así como de la velocidad y la aceleración (vectores) que poseen dirección y sentido a una nueva cantidad física: los tensores.
Las ecuaciones de campo de Einstein no son la única teoría concebida para explicar matemáticamente el fenómeno de la gravedad. Un ejemplo de otras teorías alternas lo constituye la teoría de gravitación Brans-Dicke (el principal competidor) desarrollada en 1961, la cual también es capaz de explicar la deflexión de la luz en presencia de un campo gravitacional así como la precesión de las órbitas de los planetas en torno al Sol, y contiene además características muy peculiares tales como el hecho de que la constante de gravitación universal G no es realmente una constante e inclusive lo que la sustituye dentro de la teoría Brans-Dicke puede variar de lugar así como en el tiempo. Esta teoría, a diferencia de la Relatividad General de Einstein que es una teoría de índole puramente tensorial, es una teoría escalar-tensorial en el sentido de que la interacción gravitacional depende tanto de lo que llamamos un campo escalar así como del campo tensorial propio de la Relatividad General. Ambas teorías concuerdan con los datos observados experimentalmente hasta la fecha. Sin embargo, en comparación con la fórmula tensorial básica de la Relatividad General G = 8πGT, las dos ecuaciones de la teoría Brans-Dicke:
en donde Tab es el tensor tensión-energía (o tensor energía-impulso) y φ es el campo escalar introducido en la teoría Brans-Dicke y que está ausente en la Relatividad General de Einstein, ciertamente muestran un aspecto mucho más intimidante. El consenso actual entre la mayoría de la comunidad científica es de que, a menos de que haya alguna razón importante para reemplazar a la Relatividad General Einsteniana con la más complicada teoría Brans-Dicke, no hay razones fundamentales de peso ni ventaja alguna en irnos de lo moderadamente complicado (Einstein) a lo más complejamente elaborado (Brans-Dicke y otras teorías) que, al menos filosóficamente, descansan sobre bases mucho más endebles.