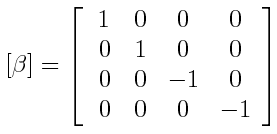Al hablar de una unificación de la Teoría de la Relatividad con la Mecánica Cuántica estamos hablando de una unificación de la Teoría Especial de la Relatividad con la Mecánica Cuántica, dejando fuera a la Relatividad General. Si bien la unificación de los conceptos básicos de la Mecánica Cuántica con las ecuaciones relativistas que describen un espacio-tiempo plano ha sido fructífera, los esfuerzos por llevar a cabo la incorporación de estos conceptos hacia un espacio-tiempo curvo ha resultado ser un verdadero dolor de cabeza sin que hasta la fecha haya producido las predicciones que en otros tiempos distinguieron a la Teoría de la Relatividad o a la Mecánica Cuántica consideradas por separado.
El primer científico en llevar a cabo la unificación de la Mecánica Cuántica con la Teoría (Especial) de la Relatividad fué Paul Adrien Maurice Dirac, mejor conocido como P. A. M. Dirac, considerado por muchos como el “padre” de la Electrodinámica Cuántica. Uno de sus más importantes logros fue la formulación de lo que podemos llamar la ecuación de onda relativista de Dirac, ecuación a la cual él mismo le dió solución mediante unos esquemas ingeniosos, logrando con ello predecir la existencia de electrones con carga positiva (antielectrones o positrones), prediciendo también que para toda partícula elemental debía existir su correspondiente antipartícula.
En este apéndice llevaremos a cabo la derivación de la ecuación de onda relativista de Dirac reproduciendo los pasos seguidos por él en lugar de utilizar el formalismo axiomático moderno que desafortunadamente tiene a obscurecer las ideas más importantes detrás de la obtención de tan importante resultado. Si bien el formalismo abstracto es más elegante, el método histórico es más intuitivo, y aquí en lo que estamos interesados es en la diseminación de las ideas fundamentales detrás del andamiaje matemático utilizado.
Aunque la explicación simplificada usualmente dada al público en general de este resultado obtenido por Dirac es que la relación “correcta” entra la masa y la energía no es la ecuación E = mc² dada por Einstein sino E² = m²c4, la cual al tomar la raíz cuadrada de ambos lados nos dá dos resultados siendo uno de ellos E = mc² (una energía positiva) y siendo el otro E = -mc² (una energía negativa), pronto se verá que esto en realidad es una sobresimplificación.
Antes de entrar en detalle sobre la ecuación de onda relativista de Dirac, es necesario repasar algunos conceptos esenciales sobre los cuales descansa la Mecánica Cuántica; específicamente la sustitución de observables (cantidades como la energía, la cantidad de movimiento, etc. que pueden ser medidas experimentalmente en el laboratorio) por operadores matemáticos, sobre lo cual el eminente físico Arno Bohm dijo lo siguiente: “La representación de observables físicas por operadores es uno de los más grandes logros de la ciencia”. Bajo este esquema, podemos tomar una ecuación de la física clásica, por ejemplo una ecuación en la cual aparezcan las tres componentes (en un sistema de coordenadas Cartesianas) del momento angular L de un cuerpo, o sea (Lx, Ly, Lz), y estas cantidades las reemplazamos por operadores matemáticos como los siguientes:
Obviamente, estos operadores matemáticos que involucran derivadas parciales de primer orden van a actuar sobre algo, van a actuar sobre un operando identificado con la letra Ψ conocido como una función de onda, y una vez que hemos montado un sistema de ecuaciones diferenciales dicho sistema puede ser resuelto para un caso en el cual las cantidades bajo consideración son cantidades muy pequeñas que corresponden al mundo sub-microscópico en el cual funcionan las reglas de la Mecánica Cuántica.
Aclarado lo anterior, estamos listos para ver cómo fue que P. A. M. Dirac obtuvo su ecuación de onda relativista. Dirac empezó con la ecuación fundamental que nos relaciona la energía total de una partícula con su momentum:
E² = (pc)² + (m0c²)²
En un sistema de coordenadas Cartesianas, el cuadrado del momentum efectivo p² es igual a la suma de los cuadrados de los componentes del momentum en los ejes Cartesianos respectivos:
p² = (px)²+ (py)²+ (pz)²
de modo tal que podemos poner la relación anterior en la siguiente forma (el subscrito cero que identifica a la masa en la expresión como una masa propia invariante será abandonado de aquí en adelante al entenderse que se trata de una masa propia):
E² = c² {(px)²+ (py)²+ (pz)² } + (mc²)²
Esto nos sugiere la forma en la cual entrarán los operadores dentro de la fórmula. Pero para ello necesitamos los operadores que nos proporciona la Mecánica Cuántica, la cual nos demuestra que las componentes rectangulares del momentum lineal pueden ser substituídas por los siguientes operadores:
en donde i = √-1. Interpretamos a un símbolo operacional como (px)² como la aplicación repetida del operador px sobre el operando:
Siendo así, entonces:
Podemos reconocer la expresión dentro del paréntesis como aquello que es usualmente simbolizado en forma abreviada con el operador de Laplace o Laplaciano:
Todo esto nos permite escribir nuestra expresión operacional tentativa:
E² = c² {-h²∇² + (mc)²}
Para escribir nuestra ecuación en forma operacional actuando sobre la función de onda, tomamos a continuación la raíz cuadrada:
E = c √-h²∇² + (mc)²
Por otra parte, de acuerdo con la Mecánica Cuántica la energía E puede ser substituída en la ecuación anterior por el siguiente operador:
Esto nos permite escribir nuestra ecuación operacional siguiente:
ih∂Ψ/∂t = c √-h²∇² + (mc)²Ψ
Aquí hemos metido ya la función de onda Ψ porque las cantidades observables han sido reemplazadas por operadores diferenciales en ambos lados. Para que esta expresión sea válida, se requiere que la función de onda sea una función tanto del tiempo como de las coordenadas Cartesianas:
Ψ = Ψ (x, y, z, t) = Ψ (r, t)
en donde r es el vector posición (x, y, z).
Al ver la expresión obtenida, Dirac concluyó que al no haber forma alguna de darle un significado físico a la raíz cuadrada de un Laplaciano la expresión dentro del radical tenía que ser forzosamente un cuadrado perfecto, de lo contrario la expresión carecía de significado. Fue así como Dirac propuso lo siguiente (hemos revertido aquí a la representación de los operadores cuánticos de los momentums como pi para simplificar el desarrollo):
(px)²+ (py)²+ (pz)² + m0²c² = (αxpx + αypy + αzpz + βmc)²
siendo αx, αy, αz, y β los coeficientes desconocidos a ser evaluados comparando la expansión del cuadrado perfecto con la fórmula original.
Expandiendo la expresión del lado derecho:
(αxpx + αypy + αzpz + βmc)² =
α²xpx² + αxαypxpy + αxαzpxpz + αxβpxmc
+ αyαxpypx+ α²ypy² + αyαzpypz + αyβpymc
+ αzαxpzpx + αzαypzpy + α²zpz² + αzβpzmc
+ βαxmcpzpx + βαymcpy + βαzmcpz + β²m²c²
Resulta obvio de inmediato que los coeficientes α no pueden ser números ordinarios. Para que las dos relaciones sean válidas, es necesario primero que:α²xpx² + αxαypxpy + αxαzpxpz + αxβpxmc
+ αyαxpypx+ α²ypy² + αyαzpypz + αyβpymc
+ αzαxpzpx + αzαypzpy + α²zpz² + αzβpzmc
+ βαxmcpzpx + βαymcpy + βαzmcpz + β²m²c²
α²x = α²y = α²z= β² = 1
Además, todos los coeficientes “fuera de la diagonal principal” (unidos a términos “cruzados” como pxpy) deben anticonmutar (a Dirac se le atribuye al invención de la palabra) para que se puedan cancelar mutuamente, o sea:
αxαy = - αyαz
αxαz = - αzαx
αyαz = - αzαy
αxαz = - αzαx
αyαz = - αzαy
Lo único en matemáticas que puede llenar tales requerimientos son las matrices, las cuales tienen la propiedad de que sus productos por regla general no son conmutativos (a menos de que una de las matrices sea la inversa de la otra, o que sea la matriz identidad o la matriz cero) y que multiplicadas por sí mismas pueden dar la unidad en caso de ser sus propias inversas. La pregunta obvia es ahora: ¿qué matrices pueden llenar estos requerimientos aquí? Como puede verse en lo que hemos desarrollado hasta este punto, Dirac estaba entrando ya en un terreno teórico que no había sido explorado previamente.
Dirac demostró que no existe un conjunto de cuatro matrices 2x2 como tampoco existe un conjunto de cuatro matrices 3x3 que puedan satisfacer los requerimientos arriba indicados. Dirac se vió entonces en la necesidad de recurrir a matrices 4x4 para poder encontrar los coeficientes α y β que hicieran posible la expresión obtenida. Después de estar trabajando un buen tiempo probando varias combinaciones posibles de matrices, Dirac encontró que las siguientes matrices podían resolver el asunto:
Estas cuatro matrices son conocidas como las matrices de Dirac. Obsérvese que cada una de estas cuatro matrices multiplicada por sí misma nos produce la matriz identidad (o matriz unitaria), cumpliéndose uno de los requerimientos señalados arriba. Obsérvese también que las matrices anti-conmutan. Además, una operación que emplea matrices 4x4 no puede ser efectuada a menos de que el operando, la función de onda Ψ, sea una cantidad que conste de cuatro componentes, como en un vector columna (una matriz 1x4):
Las funciones Ψi reciben el nombre especial de espinores (spinors).
Habiendo comprobado la existencia de un cuadrado perfecto para todo el término que aparecía bajo la raíz cuadrática, podemos reemplazar dicho cuadrado perfecto dentro de la raíz para así extraerla metiendo nuevamente tras esto los operadores del momentum px, py y pz obteniendo:
Esta es una ecuación cuántica-relativista dependiente del tiempo. Para hacerla independiente del tiempo, recurrimos a una técnica matemática usal en estos casos, la separación de variables, separando la variable original Ψn en el producto de una función ψn dependiente únicamente del vector posición r pero independiente del tiempo, multiplicada por otro factor dependiente del tiempo:
Ψn(r,t) = ψn(r) · e-iEt/h
que en nuestro caso para las cuatro componentes de la función de onda representada como un vector columna viene siendo:
La ventaja de utilizar la función e-iEt/h radica en el hecho de que al tomar la derivada parcial de dicha función con respecto al tiempo nos queda como factor la misma función, lo cual permite cancelarla al aparecer en ambos lados de la ecuación matricial.
En la simplificación que se está llevando a cabo, es necesario obtener como resultado intermedio los siguientes productos de cada matriz [αn] por el vector columna ψ en ese orden (recuérdese que el producto de dos matrices no es conmutativo, y en este caso estamos post-multiplicando cada una de las matrices 4x4 de Dirac por un vector columna que es en realidad una matriz 4x1, lo cual nos debe producir en cada caso una matriz 4x1):
Es así como se llegamos a la siguiente ecuación:
Esta es la ecuación de onda relativista de Dirac, conocida simplemente como ecuación de Dirac. Puesto que dos matrices son iguales cuando sus elementos correspondientes son iguales, la ecuación matricial de arriba en realidad corresponde a un conjunto de cuatro ecuaciones diferenciales parciales acopladas. En pocas palabras, la ecuación de Dirac en realidad es un conjunto de cuatro ecuaciones distintas y no una sola ecuación.
Como puede verse, una cosa es montar una ecuación como lo hizo Einstein con G = 8πGT, y otra cosa es desenvolver la ecuación encontrándole soluciones. Es aquí cuando los teóricos necesitan aplicar todo su ingenio al refinamiento o inclusive a la edificación del aparato matemático que se necesita para poder llegar a algún lado. Fue así como Newton se vió en la necesidad de tener que inventar por cuenta propia el cálculo infinitesimal (un mérito que se estuvo disputando con Leibnitz hasta el final de sus días) para poder obtener fórmulas básicas para la explicación del movimiento de los planetas en base a su ley de gravitación universal, y fue así como Einstein se vió en la necesidad de concebir trucos ingeniosos para poder obtener una solución al problema de las mismas órbitas planetarias descritas ahora por sus ecuaciones de campo.
Podemos obtener una solución a la ecuación de Dirac (o mejor dicho, al conjunto de ecuaciones diferenciales acopladas de Dirac) considerando el caso de una partícula libre viajando a lo largo de cierto eje (lo cual nos permite ignorar los otros dos ejes). Para una partícula libre que viaja a lo largo del eje-z, la ecuación de onda relativista de Dirac se reduce a lo siguiente:
El dilema ahora es determinar la manera en la cual vamos a representar matemáticamente una partícula libre. Cuando se trata de una partícula confinada dentro de un contenedor cerrado, esto no representa ningún problema, ya que en virtud de la naturaleza ondulatoria de la partícula en su dualidad onda-partícula, no puede haber cantidades fraccionarias de onda dentro del contenedor cerrado, solo puede haber múltiplos enteros de una frecuencia básica (al igual que en una guitarra cuando hacemos sonar una cuerda), esto es precisamente lo que determina la cuantización (o discretización) de los niveles de energía de la partícula. Pero cuando la partícula está libre viajando de un lugar a otro, no es fácil representarla como una onda viajera de una frecuencia específica. Para resolver este asunto, Dirac concibió una función que desde su creación no ha sido muy del agrado de los matemáticos por su naturaleza impropia, la función Dirac delta o función-δ de Dirac. Es una función límite que podemos imaginar como un rectángulo de área unitaria al cual le vamos acortando su base y le vamos agrandando su altura manteniéndo el “área bajo la curva” igual a la unidad, hasta que su anchura es infinitamente pequeña y su altura es infinitamente grande, manteniéndose el “área bajo la curva” igual a la unidad al hacer tender la anchura y la altura hacia lo infinitamente pequeño y lo infinitamente grande respectivamente. Esta función representa, en efecto, una discontinuidad en el espacio-tiempo suave que requiere la Relatividad General para poder funcionar. Toda partícula sub-atómica es, en efecto, una discontinuidad en el espacio-tiempo en la cual la maquinaria matemática utilizada por Einstein en su formulación de la Relatividad General deja de ser válida.
Una onda estacionaria (conocida en la literatura inglesa como standing wave) se puede representar con cualquiera de las siguientes dos funciones trigonométricas:
y(x) = A sen(x)
y(x) = A cos(x)
y(x) = A cos(x)
en donde A es la amplitud de la onda estacionaria. El siguiente gráfico muestra ambas con una amplitud de A = 1, con la onda senoidal en color rojo y la onda cosenoidal en color azul:
Podemos convertir una onda estacionaria en una onda viajera con la simple adición de un término que va cambiando con el tiempo:
y(x) = A sen(x - ωt)
y(x) = A cos(x - ωt)
y(x) = A cos(x - ωt)
En estos casos, tenemos ondas viajeras que se van desplazando de izquierda a derecha. Si queremos que las ondas se desplazen de derecha a izquierda, todo lo que tenemos que hacer es cambiar el signo negativo por uno positivo.
Podemos multiplicar en las ecuaciones de arriba la variable independiente por un factor de escala k sin que esto altere la esencia de la representación gráfica de las ondas viajeras:
y(x) = A sen(kx - ωt)
y(x) = A cos(kx - ωt)
y(x) = A cos(kx - ωt)
Empleando la relación de Euler:
eiθ = cos(θ) + i sen(θ)
podemos representar una onda viajera en su forma más general del modo siguiente:
ψ(x, t) = Aei(kx - ωt)
Sin embargo, esta relación nos representa una onda que se extiende con la misma amplitud hacia el infinito en dos direcciones, hacia la derecha y hacia la izquierda. Y nosotros lo que queremos representar matemáticamente es algo conocido como un paquete de onda (wave packet) que no se extiende hasta el infinito en dos direcciones opuestas:
como correspondería a una partícula que es esencialmente una onda de materia. Esto lo podemos lograr si nos damos cuenta de que la adición de dos ondas de frecuencias diferentes produce un “batido” repetitivo cuya frecuencia de repetición dependerá de las frecuencias de las ondas originales:
En el diagrama de arriba sólo hemos agregados dos ondas con frecuencias ligeramente diferentes. Si vamos agregando una cantidad adicional de ondas cada “paquete de onda” se irá alejando más y más de sus paquetes de onda vecinos, hasta que en los extremos cercanos al infinito nuestro paquete de onda se encontrará prácticamente solo. Eventualmente, la suma se convierte en una integral representándonos a la partícula como un paquete de onda viajero. De este modo, la partícula libre, como fue concebida por Dirac, es el resultado de una superposición de un espectro infinito de frecuencias que por efectos de cancelación y adición adquieren una amplitud máxima precisamente en la misma partícula. Existe una teoría matemática para justificar esta representación de una partícula en el dominio frecuencia en lugar del dominio tiempo. Se llama análisis de Fourier, y en dicha rama de las matemáticas (que no es más que una extensión de las series de Fourier en donde las sumatorias de las series son reemplazadas por integrales mediante las transformadas de Fourier), se puede tomar una función que varía con el tiempo f(t) y se puede encontrar su representación equivalente en el dominio frecuencia g(ω). Para una partícula libre caracterizada por un momentum preciso p = hk en donde k es el número de onda definido como k = 2π/λ (inversamente proporcional a la longitud de onda), dicha partícula puede ser representada como el paquete de onda de una función-δ. Matemáticamente, para una partícula viajando a lo largo del eje-z, la representación es la siguiente:
Ψ(z,t) = √2π ∫A(k) e-i(ωt - kz) dk
que en el caso que nos ocupa podemos escribir para cada una de las cuatro ecuaciones matriciales de Dirac como:
[Ψn(z,t)] = [An] e-i(ωt - kz) dk
[Ψn(z,t)] = [An] eikz e-iEt/h dk
[Ψn(z,t)] = [An] eikz e-iEt/h dk
Si substituímos esta última expresión en la ecuación de Dirac para una partícula viajando a lo largo del eje-z tendremos entonces lo siguiente:
Puesto que el vector columna de las amplitudes An no es igual al vector cero, el determinante de la matriz simétrica debe ser igual a cero. Obteniendo dicho determinante e igualándolo a cero tenemos entonces:
(E² - m²c4 - c4h²k²)² = 0
y puesto que p = hk, esto nos dá para la energía de la partícula:
E = ± {p²c² + m²c4} 1/2 = E±
A diferencia de otros problemas en la física clásica en donde descartamos mediante consideraciones lógicas una de las soluciones obtenidas tras la extracción de una raíz cuadrada con sus consecuentes dos signos, el positivo y el negativo, en este caso la raíz negativa nos dá soluciones con significado físico. El signo negativo puede ser identificado con el electrón que posee una carga eléctrica negativa y el signo positivo puede ser identificado con el positrón que posee una carga eléctrica positiva. Siendo así, la ecuación de onda relativista de Dirac predice la existencia del positrón. Y no solo esto, predice la existencia de la antimateria.
Para una partícula confinada dentro de una barrera de potencial con paredes infinitamente altas (lo cual se puede tratar como un problema en una sola dimensión) separadas por una distancia L, no presenta mucha dificultad el determinar que la ecuación de onda relativista de Dirac predice niveles de energía proporcionados por la siguiente relación:
W = ± {m0c² + h²k²π²/2m0L²}
Esta expresión difiere del resultado cuántico clásico (pre-relativista) por el término m0c² que representa la masa en reposo de la partícula. Y predice niveles de energía iguales pero opuestos en signo para la partícula y su antipartícula.
Tras la ecuación de onda de Dirac, no tardaron en llegar otras ecuaciones tales como la ecuación Klein-Gordon que pasarían a formar el catálogo de conocimientos hoy conocido como la Mecánica Cuántica Relativista. Pero todo este material está basado, ultimadamente, en la unificación de la Mecánica Cuántica con la Teoría Especial de la Relatividad como lo hemos visto aquí. La unificación con la Relatividad General es otro asunto que sigue pendiente de resolverse. El mismo Einstein no pudo visualizar cómo se podría llevar a cabo esto, si es que se puede llevar a cabo. Y si se puede llevar a cabo ya sea con la introducción de nuevos conceptos o con la invención de nuevas herramientas matemáticas, se pueden esperar predicciones de efectos tan espectaculares como los desarrollos teóricos previos han logrado materializar.