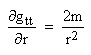Nuevamente, consideraremos una región del espacio en torno a una masa puntual estática, para la cual podemos suponer que la métrica tiene una simetría esférica perfecta e independiente del tiempo. Y con la finalidad de simplificar la derivación que será llevada a cabo, recurriremos al uso de unidades geometrizadas con las cuales se fija a la constante velocidad de la luz c con un valor igual a la unidad, o sea c = 1.
Aún sin conocer las ecuaciones de campo de la Relatividad General, es posible dar una derivación “heurística” (más artística que técnica) no totalmente rigurosa de la métrica de Schwarzschild conociendo de antemano la característica de la variación de la gravedad con el inverso del cuadrado de la distancia, el conocimiento previo de la tercera ley de Kepler para órbitas circulares, y los intervalos nulos para trayectorias luminosas.
Designaremos a r como la coordenada espacial radial (la distancia a la masa puntual) de modo tal que cada punto en una superficie de r constante tenga la misma geometría intrínseca y la misma relación a la masa puntual a la cual situamos en el punto r = 0. Designemos también como t a nuestra coordenada temporal. Cualquier superficie de r y t constantes debe poseer la geometría intrínseca bi-dimensional de una 2-esfera, y podemos graduar el parámetro radial de modo tal que el área superficial sea 4πr². (Puesto que a estas alturas el 4-espacio no es necesariamente Euclideano, no estamos afirmando que r sea la “distancia radial” desde la masa puntual. Más bien r es una coordenada radial arbitraria ajustada para darnos el área superficial Euclideana que corresponde a una 2-esfera.) Con este ajuste de escala, podemos parametrizar la 2-superficie para cualquier valor de r y de t mediante la métrica esférica ordinaria de “latitud y longitud”:
ds² = r² (dθ)² + r² sen² θ (dφ)²
en donde ds representa la distancia incremental sobre la superficie de una esfera ordinaria de radio r que corresponda a desplazamientos incrementales dθ y dφ. La coordenada θ representa la “latitud” con θ = 0 en el polo Norte y θ = π/2 en el Ecuador, y la coordenada φ representa la “longitud” relativa a cierto meridiano arbitrario. En base a esto podemos decir que la métrica completa del tiempo-espacio en la cercanía de una masa esféricamente simétrica debe tener la forma:
ds² = gtt(dt)² + grr(dr)² + gθθ(dθ)² + gφφ(dφ)²
en donde gθθ = - r² y gφφ = - r² sen² θ, y tanto gtt como gφφ son funciones desconocidas de r y de la masa central m. Naturalmente, si hacemos m = 0 entonces ambas funciones gtt y grr deben ser iguales a la unidad para que puedan darnos la métrica de un espacio-tiempo plano, Lorentziano, puesto que esperamos que la métrica se vaya aplanando a distancias lo suficientemente alejadas de la masa gravitacional.
Puesto que la métrica es diagonal, los componentes que corresponden al tensor métrico conjugado g-1 = (gab) están dados simplemente por gaa = 1/gaa. La diagonalidad de la métrica nos permite simplificar los símbolos de Christoffel a la siguiente relación (ni en gαα ni en ninguna otra parte de la ecuación hay sumación alguna implicada):
Por otro lado, las derivadas parciales de los coeficientes métricos que no terminan siendo cero son las siguientes:
ajunto con ∂gtt/∂r y ∂grr/∂r que están aún por ser determinados. Insertando estas derivadas parciales en la ecuación anterior encontramos que los únicos símbolos de Christoffel que no son cero son los siguientes:
De esto obtenemos los coeficientes para las cuatro ecuaciones geodésicas que corresponden a un 4-espacio en la cercanía de una masa esféricamente simétrica, que son:
Aquí suponemos que en ausencia de fuerzas no-gravitatorias, todos los movimientos naturales (tanto partículas con masa como fotones luminosos) siguen rutas geodésicas, de modo tal que este sistema de ecuaciones nos proporciona una descripción completa de los movimientos inerciales-gravitatorios de partículas de prueba en un campo esféricamente simétrico. Todo lo que nos queda por determinar son los coeficientes gtt y grr, y para lograrlo es aquí cuando recurriremos a la tercera ley de Kepler que nos dice: “Para cualquier planeta siguiendo una órbita elíptica, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del Sol) es directamente proporcional al cubo de la distancia media con el Sol (o la masa central que está ejerciendo la atracción gravitatoria)”. Esperamos que una posible solución a la métrica que estamos tratando de especificar sean órbitas Keplerianas circulares, lo cual significa que si consideramos a r correspondiendo al menos aproximadamente a la distancia Newtoniana radial al centro de la masa puntual, entonces debe de haber una ruta geodésica circular llevándose a cabo a una distancia r constante con una velocidad angular ω, y estas cantidades tienen que estar relacionadas -al menos aproximadamente- según la tercera ley de Kepler de acuerdo con la siguiente fórmula empírica para dicha ley:
m = r3 ω²
Si consideramos un movimiento puramente circular llevándose a cabo en el plano Ecuatorial (θ = π/2) a un valor de r constante, entonces la métrica se reduce a:
ds² = gtt(dt)² - r² (dφ)²
Recurriremos ahora al tiempo propio (tiempo local ) haciendo ds² = (cdτ)². Si hacemos c = 1 para fines de simplificación en la demostración, tenemos entonces lo siguiente:
dτ² = gtt(dt)² - r² (dφ)²
Puesto que dr/dt = o al no variar la coordenada radial conforme la partícula de prueba se mueve a lo largo de la ruta geodésica circular, las ecuaciones geodésicas para estas rutas circulares se reducen a:
Multiplicando al través por (dτ/dt)² e identificando a la velocidad angular ω con la derivada de φ con respecto a la coordenada temporal t, el lado derecho de esta última relación se convierte en:
Para que haya consistencia con la tercera ley de Kepler, tenemos que tener a ω² igual (o aproximadamente igual) a m/r3, de modo tal que llevamos a cabo esta substitución arriba para obtener:
Integrando esta ecuación encontramos que el coeficiente métrico debe ser de la forma:
k - (2m/r)
en donde k es una constante de integración. Puesto que gtt debe ser igual a 1 cuando m = 0 y/o cuando r tiende hacia el infinito, resulta claro que k = 1, de modo tal que:
Tenemos también que para un fotón alejándose en una dirección puramente radial de la masa gravitatoria dτ = 0, de modo tal que nuestra métrica para un rayo de luz puramente radial debe ser:
gtt(dt)² = - grr(dr)²
Considérese ahora una partícula radial de prueba situada a una distancia radial r. La ecuación de la métrica proporciona el elemento de línea de la línea del mundo (diagrama espacio-tiempo de Minkowski) de esta partícula de prueba:
dτ² = gtt dt²
y tenemos también la ecuación de la ruta geodésica radial para esta partícula:
El lado izquierdo de esta ecuación es la aceleración causada por la gravedad, dr²/dτ² en unidades geométricas (con c= G = 1), lo cual es considerado como la expresión del inverso del cuadrado de la distancia - m/r² (el signo negativo sirve para distinguir la fuerza atractiva en contraste con la fuerza repulsiva). Combinando esto con las relaciones anteriores obtenemos entonces:
gtt grr = - 1
Esto implica una “factorización perpendicular” de gtt = dr/dt y grr = - dr/dt en gtt(dt)² = - grr(dr)², lo cual nos dá grr = - 1/gtt, con lo cual tenemos ya la métrica completa de Schwarzschild:
dτ² = (1 - 2m/r)(dt)² - (1 - 2m/r) -1(dr)² - r² (dθ)² - r² sen² θ (dφ)²
en unidades geometrizadas en donde la masa m tiene unidades de longitud.
El que sea posible derivar la métrica de Schwarzschild a partir de las leyes de Kepler sin tener un conocimiento previo de las ecuaciones de campo de la Relatividad General es posible porque los resultados obtenidos mediante las ecuaciones de campo de la Relatividad General se deben reducir a los resultados clásicos cuando el campo gravitacional no es muy intenso. Naturalmente, esto tiene sus limitaciones, porque en el caso de la luz, careciendo los fotones de masa en reposo, la mecánica Newtoniana no produce efecto gravitatorio alguno sobre la luz, en contraposición directa con lo que predice la Relatividad General.
PROBLEMA: Obtener los símbolos de Christoffel de segundo género que sean diferentes de cero para la métrica de Schwarzschild dada como:
ds² = (1 - 2GM/rc²) c²dt² - [1 - 2GM/rc²] -1 dr² - r² dθ - r² sen² θ dφ²
De este elemento de línea ds² de la métrica de Schwarzschild obtenemos los componentes del tensor métrico g que corresponde a dicha métrica, cuya representación matricial es la de una matriz diagonal:
La fórmula general para la evaluación de los símbolos de Christoffel es:
Γαμν = gαβ (- gμν,β + gνβ,μ + gμβ,ν)/2
Γαμν = gαβ (- ∂gμν/∂xβ + ∂gνβ/∂xμ + ∂gμβ/∂xν)/2
o bien, mostrando explícitamente las diferenciaciones parciales sin recurrir a la abreviatura de la notación de la coma:
Γαμν = gαβ (- ∂gμν/∂xβ + ∂gνβ/∂xμ + ∂gμβ/∂xν)/2
Para la evaluación de Γ111 en cooordenadas generalizadas tenemos:
Γ111 = g11 (- ∂g11/∂x1 + ∂g11/∂x1 + ∂g11/∂x1)/2
o bien, haciendo a un lado las coordenadas generalizadas:
Aunque podemos evaluar todos los símbolos de Christoffel mediante la relación general, en la obtención abreviada de los símbolos de Christoffel de segundo género para un tensor métrico cuya representación matricial es la de una matriz diagonal podemos utilizar las relaciones de cálculo abreviado que se reproducen a continuación (no aplica en estas fórmulas la convención de sumación para índices repetidos):
El primer símbolo de Christoffel que obtendremos usando estos atajos será el que corresponde a Γttr que por la propiedad de simetría para los símbolos de Christoffel de segundo género es igual a Γtrt :
Ahora evaluaremos el símbolo de Christoffel que corresponde a Γrtt (en la segunda línea el signo negativo de la primera línea es cancelado por el signo negativo que va con grr):
El siguiente símbolo de Christoffel que obtendremos con los atajos será el que corresponde a Γ222 = Γrrr (al aparecer repetido grr, el efecto de los dos signos negativos se cancela):
A continuación obtendremos el símbolo de Christoffel que corresponde a Γrθθ (el signo negativo que porta grr se nulifica con el signo negativo que lleva gθθ):
El siguiente símbolo de Christoffel que evaluaremos será Γrφφ (el signo negativo que porta grr se nulifica con el signo negativo que lleva gφφ):
A continuación evaluaremos el símbolo de Christoffel Γθφφ (el signo negativo que porta gθθ se nulifica con el signo negativo que lleva gφφ):
Haremos ahora la evaluación del símbolo Γθθr:
Por virtud de la simetría en los sub-índices de los símbolos de Christoffel de segundo género, en base a este resultado tenemos también que Γθθr = Γθrθ.
A continuación evaluaremos el símbolo de Christoffel Γφφr (al estar repetido gφφ en la fórmula abreviada, el efecto de los dos signos negativos se cancela):
En virtud de la simetría en los sub-índices de los símbolos de Christoffel de segundo género, en base a este resultado tenemos también que Γφφr = Γφrφ.
Por último, evaluaremos a Γφφθ:
En virtud de la simetría en los sub-índices de los símbolos de Christoffel de segundo género, en base a este resultado tenemos también que Γφφθ = Γφθφ.
Todos los demás símbolos de Christoffel posibles son iguales a cero.
Con los símbolos de Christoffel disponibles para una métrica en particular, el montaje del sistema de ecuaciones geodésicas del movimiento para el 4-espacio relativista es directo e inmediato.
PROBLEMA: Obtener las ecuaciones geodésicas correspondientes a los símbolos de Christoffel de la métrica de Schwarzschild que sean necesarias para describir el movimiento planetario de un cuerpo sumergido en un campo gravitacional.
Al tratar el tema de la ruta geodésica, vimos que para el 4-espacio usando el tiempo propio (local) τ como el parámetro independiente, es el siguiente (en coordenadas generalizadas):
Para un campo esféricamente simétrico basado en las coordenadas (x1, x2, x3, x4) = (t, r, θ, φ), el sistema de ecuaciones geodésicas es el siguiente:
En cada una de las cuatro ecuaciones, por la convención de sumatoria para índices repetidos tendríamos en principio para el segundo término una expansión a 16 términos, y siendo cuatro las ecuaciones geodésicas del movimiento tendríamos que escribir un total de 4x16 = 64 términos adicionales para su posterior simplificación algebraica, lo cual puede parecer intimidante. Sin embargo, como podemos verlo en los símbolos de Christoffel que obtuvimos arriba para la métrica de Schwarzschild, en realidad hay tan solo unos cuantos que son diferentes de cero, de modo que el trabajo real es mucho menor de lo que aparenta ser.
Llevaremos a cabo la formulación de la primera ecuación geodésica, la que corresponde a la primera coordenada (temporal) t:
escribiendo simplemente 0 para representar los 14 términos que son iguales a cero en la sumatoria desarrollada sin tomarnos la molestia de escribirlos explícitamente:
Del mismo modo, para la coordenada φ la ecuación geodésica será obtenida de la siguiente manera:
La evaluación de la ecuación geodésica que corresponde a la coordenada radial r, con las sumatorias expandidas de acuerdo a como lo pide la convención de sumación para índices repetidos:
y que viene siendo igual a la siguiente expresión simplificada:
resulta ser la siguiente:
Podemos hacer una ligera simplificación de esta ecuación geodésica escribiéndola de la siguiente manera:
Si a estas alturas recurrimos a unidades geometrizadas (haciendo G = 1 y c = 1) con las cuales podemos acortar lo que tenemos que escribir, podemos escribir las siguientes ecuaciones geodésicas abreviadas para la métrica de Schwarzschild:
No hemos obtenido aún la ecuación geodésica que corresponde a d²θ/dτ². En realidad, no la necesitamos. Y no la necesitamos porque el movimiento del cuerpo en su ruta geodésica a través del espacio-tiempo curvo se lleva a cabo en un plano, requiriéndose por lo tanto una sola coordenada angular para continuar con el análisis. De cualquier modo, y con fines de completitud, a continuación tenemos la ecuación geodésica para la coordenada angular θ:
Obsérvese que si llevamos a cabo nuestro análisis en un plano de movimiento para el cual θ = π/2, el segundo término en esta última ecuación se desvanece en virtud de que cos(π/2) = 0, y la ecuación geodésica se reduce a lo mismo que lo que ya tenemos para la ecuación geodésica correspondiente a la coordenada φ, lo cual era de esperarse en virtud de que no hay razón por la cual un desplazamiento angular deba ser privilegiado sobre otro.
Continuaremos nuestro análisis recurriendo a las unidades geometrizadas que nos permiten tomar a la velocidad de la luz c y a la constante de gravitación universal G con valores iguales a la unidad, o sea c = G = 1. El uso de unidades geometrizadas está justificado cuando lo que queremos hacer es llevar a cabo un análisis cualitativo como lo haremos a continuación. Si lo que queremos es obtener resultados numéricamente exactos en unidades convencionales, entonces tenemos que revertir a los valores físicos reales de G y de c.
Podemos integrar de inmediato -con substitución de variables- la primera ecuación y la tercera ecuación geodésicas para obtener así, en unidades geometrizadas:
en donde k y h son constantes de integración determinadas por las condiciones iniciales de las órbitas. Por otro lado, si con el fin de seguir llevando a cabo nuestro análisis cualitativo (en lugar de un análisis cuantitativo con resultados numéricos reales) tomamos la métrica convencionalmente “correcta” de Schwarzschild:
ds² = (1 - 2Gm/rc²)(cdt)² - (1 - 2Gm/rc²) -1(dr)²
- r² (dθ)² - r² sen² θ (dφ)²
- r² (dθ)² - r² sen² θ (dφ)²
haciendo ds = cdτ:
(cdτ)² = (1 - 2Gm/rc²)(dt)² - (1 - 2Gm/rc²) -1(dr)²
- r² (dθ)² - r² sen² θ (dφ)²
- r² (dθ)² - r² sen² θ (dφ)²
y la expresamos en unidades geometrizadas haciendo G = 1 y c = 1:
dτ² = (1 - 2m/r)(dt)² - (1 - 2m/r) -1(dr)²
- r² (dθ)² - r² sen² θ (dφ)²
- r² (dθ)² - r² sen² θ (dφ)²
dividiendo tras esto a la métrica entre dτ², obtenemos entonces lo siguiente:
1 = (1 - 2m/r)(dt/dτ)² - (1 - 2m/r) -1(dr/dτ)²
- r² (dθ/dτ)² - r² sen² θ (dφ/dτ)²
- r² (dθ/dτ)² - r² sen² θ (dφ/dτ)²
Escogiendo para θ un valor constante θ = π/2, con lo cual dθ/dτ = 0, y con lo cual el último término se reduce simplemente a r² (dφ/dτ)², tenemos entonces:
1 = (1 - 2m/r)(dt/dτ)² - (1 - 2m/r) -1(dr/dτ)² - r² (dφ/dτ)²
Substituyendo aquí los resultados que obtuvimos de las integraciones de las dos ecuaciones geodésicas para la métrica de Schwarzschild, llegamos ahora a lo siguiente:
Podemos despejar para (dr/dτ)², obteniendo así:
Diferenciando esto último con respecto a τ y dividiendo entre 2(dr/dτ) obtenemos lo siguiente:
Haciendo dφ/dτ = ω para identificar a la velocidad angular propia (local), podemos identificar entonces que h = ωr², con lo cual esta última ecuación puede ser escrita de la siguiente manera:
Para el caso en el que la velocidad angular del cuerpo que está sumergido en la métrica es igual a cero, o sea ω = 0, esto nos dá la forma apropiada de la ley de la atracción universal de Newton en la cual la aceleración gravitacional varía en razón inversa al cuadrado de la distancia. Para el caso en el que ω no es igual a cero, el término ω²r corresponde a la aceleración centrípeta Newtoniana clásica para la cual, si definiéramos a la velocidad tangencial como el producto de la velocidad angular por el radio (v = ωr), sería igual a la expresión clásica v²/r. Este término sirve para contrarrestar de alguna manera la atracción causada por la gravedad, pero en la versión relativista exacta lo que encontramos no es ω²r sino ω²(r - 3m) en el tercer término de la ecuación de arriba. Para evitar confusiones, vale la pena notar que la cantidad ω²(1 - 3m/r) sería simplemente ω² si ω fuese definida como la derivada de φ con respecto al tiempo de coordenada de Schwarzschild (t) en lugar del tiempo propio τ. De este modo, la versión relativista de la tercera ley de Kepler para órbitas circulares es formalmente idéntica a la versión Newtoniana, pero solo si identificamos a las coordenadas Newtonianas con las coordenadas de Schwarzschild. Para valores de r mucho mayores que 3m -en unidades geometrizadas- esta diferencia puede ser ignorada, pero debe ser claro que conforme el valor de r se va aproximando cada vez más al valor de 3m podemos esperar encontrarnos con efectos no-clásicos, y naturalmente si r llega a ser menor que 3m esperamos encontrarnos con efectos de índole puramente relativista que no tienen absolutamente nada de clásicos. De hecho, esto corresponde al caso en el cual la partícula en órbita va cayendo en espiral hacia el centro. En la mecánica clásica Newtoniana, es imposible que una partícula en órbita pueda ir cayendo en espiral hacia el centro del cuerpo que produce el campo gravitacional porque sólo son posibles las órbitas elípticas. Aunque se nos vengan a la mente las imágenes de satélites en órbita que van cayendo en espiral hacia la Tierra (como el Skylab, precursor de la Estación Espacial Internacional, el cual cayó a la tierra el 11 de julio de 1979 tras ir perdiendo altura por varias semanas), la pérdida de altura en tales casos se debe a la oposición que va presentando la cada vez más densa atmósfera terrestre al satélite que está cayendo. La caída en espiral no sólo es posible sino que incluso es explicada y anticipada dentro de la mecánica relativista.
Puesto que las ecuaciones de arriba involucran únicamente potencias de (1/r), es conveniente hacer un cambio de variables haciendo u = 1/r. Diferenciando a u con respecto a φ nos dá du/dφ = -(1/r)²dr/dφ. También, puesto que r² = h/(dφ/dt), tenemos que dr/dτ = -h(du/dφ). Substituyendo los valores de dr/dτ y 1/r en la ecuación:
obtenemos la siguiente ecuación diferencial que nos relaciona a u con φ:
Diferenciando nuevamente con respecto a φ y dividiendo entre 2h² llegamos a lo siguiente:
en donde con la notación de doble punto estamos representando lo siguiente (no se trata de una segunda derivada con respecto al tiempo):
Lo que tenemos ahora es una ecuación cuadrática en u. Resolviendo dicha ecuación cuadrática tenemos entonces:
La cantidad dentro de los paréntesis bajo la raíz cuadrada típicamente es muy pequeña en comparación con la unidad, de modo tal que podemos aproximar a la raíz cuadrada con los primeros términos de la expansión en series:
Usando estas aproximaciones para expandir el lado derecho y reacomodando términos obtenemos entonces:
El valor de d²u/dφ² es numéricamente muy pequeño en problemas astronómicos típicos, varios órdenes de magnitud menor que la unidad, de modo tal que la cantidad 3m(d²u/dφ²) en el lado derecho puede ser ignorada en el análisis de los movimientos planetarios. Esto nos deja ya simplmente con un oscilador harmónico simple de la forma:
en donde M y F son constantes. Para alguna selección inicial de φ la solución general de esta ecuación puede ser expresada de la manera siguiente:
en donde k es una constante de integración. De este modo, revirtiendo al parámetro original r = 1/u, la relación entre r y φ es:
en donde:
Si la “frecuencia” ω del movimiento planetario fuese igual a la unidad, esto vendría siendo la ecuación en coordenadas polares de una elipse con el polo ocupando uno de los focos de la elipse (primera ley de Kepler), y la constante k sería la eccentricidad. Por su parte, el factor principal vendría siendo la distancia radial del foco a la elipse a un ángulo de π/2 radianes del eje mayor; o en otras palabras, vendría siendo el semilatus rectum. Sin embargo, el valor de ω es de hecho ligeramente menor que la unidad, lo que implica que φ debe ir un poco más allá de 2π para poder completar un ciclo de la distancia radial. Consecuentemente, para valores pequeños de m/h la trayectoria es aproximadamente Kepleriana, pero el eje está sujeto a una precesión como lo muestra la siguiente figura:
Esta figura muestra un caso mucho más severo que el que existiría para cualquier planeta en nuestro sistema solar, porque el perihelio de la órbita de este ejemplo está a únicamente 200m (en donde m es el radio gravitacional en unidades geometrizadas) del cuerpo central, lo cual significa que está a únicamente unas 100 veces del “radio del agujero negro correspondiente” (posteriormente se verá con más detalle el caso de los agujeros negros). La masa de nuestro propio Sol no está lo suficientemente concentrada para permitir este tipo de órbita con una precesión tan pronunciada, puesto que el radio gravitacional del Sol es de únicamente m = 1.475 kilómetros, mientras que su masa se extiende a una esfera de 696 mil kilómetros de radio.
Para determinar la predicción relativista para la precesión de las órbitas planetarias, podemos llevar a cabo la expansión de W del modo siguiente:
Puesto que m/h es tan pequeño, podemos tomar simplemente el término de primer orden, y observando que un ciclo de la función radial será completado cuando ωφ = 2π, podemos ver que φ debe incrementar en 2π/ω para cada ciclo radial, de modo que la precesión por revolución viene siendo:
A diferencia de la aproximación utilizada por Einstein para el cálculo de la precesión de Mercurio, la solución de Schwarzschild es una solución exacta, lo que significa que puede ser utilizada en el análisis de los movimientos planetarios en donde el cuerpo central puede ser un cuerpo masivo compacto produciendo un campo gravitacional mucho más intenso que el del mismo Sol. Si nos imaginamos tal objeto central extremadamente denso, cuya masa esté concentrada dentro de su radio gravitaciona, podemos obtener desviaciones mucho mayores de las órbitas Newtonianas. Si la razón de la precesión es aproximadamente igual a la razón orbital, entonces tendremos una órbita como la que se muestra a continuación:
Para una órbita con una energía ligeramente menor, la trayectoria tendrá un aspecto como el siguiente:
en donde el círculo interior punteado representa la órbita “ligera” con el radio r = 3m. Con suficiente momentum angular es posible hacer que órbitas persistentes tipo-tiempo (timelike) vayan descendiendo hacia el cuerpo central a cualquier radio provisto que se mayor que 3m, el cual a su vez es el radio más pequeño posible para una órbita circular (de cualquier modo, una órbita circular para un radio menor que 6m se vuelve inestable). Si una geodésica tipo-tiempo llega a pasar dentro de tal radio entonces recorrerá una trayectoria en espiral hacia el cuerpo central como lo muestra la siguiente figura:
En este ejemplo, el círculo punteado exterior representa el valor 3m (esto tiene que ver con algo que ha sido definido como la esfera de fotones y lo cual estudiaremos posteriormente con mayor detalle), mientras que el círculo interior está situado en el valor 2m justo en lo que se conoce como el horizonte de evento de los agujeros negros (en dimensiones “correctas”, el valor 2m viene siendo la distancia rs = 2GM/c² conocida como el radio de Schwarzshild y la cual estudiaremos posteriormente con mayor detalle) dentro del cual no le es posible a nada escapar ni siquiera a la misma luz. Una vez que una línea del mundo ha caído dentro de 2m, trátese o no de una geodésica, la coordenada radial de acuerdo con la solución de Schwarzschild debe ir disminuyendo monotónicamente hacia cero. El asunto de los agujeros negros es de una importancia tal que su discusión será tratada más a fondo posteriormente.
En relación a la caída en espiral hacia el cuerpo central generador del campo gravitacional, hay un precedente histórico curioso sobre esto. Algún tiempo antes de escribir su Principia en donde las bases de la mecánica Newtoniana gravitacional quedaron establecidas, Newton escribió una carta a Robert Hooke describiéndole la caída en espiral de un objeto hacia el centro de un cuerpo ejerciendo una atracción gravitacional. Años después cuando Principia había establecido la reputación de Newton, ambos se enfrascaron en una discusión acalorada sobre quién tenía el mérito del descubrimiento de las leyes (clásicas) de la gravitación universal, y Hooke frecuentemente citaba la carta de Newton como evidencia de que en ese tiempo Newton no había entendido lo suficientemente bien la naturaleza de la gravedad, en virtud de que la ley de la inversa del cuadrado de la distancia no permite caídas en espiral, sólo permite órbitas elípticas. Newton simplemente respondió argumentando que tal idea había sido simplemente un golpe desafortunado de su pluma. Resulta interesante notar que aunque en ocasiones hay gente que le atribuye a Newton la idea de los fotones basada en su errónea teoría corpuscular de la luz (los corpúsculos de Newton requerían estar formados de masa, y hoy se sabe que los fotones carecen de masa en reposo) jamás se ha sugerido que la “espiral negligente” de Newton haya sido una premonición de la caída en espiral predicha por la solución de Schwarzschild a las ecuaciones de campo de la Relatividad General.
En los desarrollos que hemos llevado a cabo, se ha supuesto que el campo gravitacional del cuerpo central que genera el espacio-tiempo curvo correspondiente a la métrica de Schwarzschild es de mucho mayor intensidad que la intensidad de los campos que provocan las curvaturas del espacio-tiempo que acarrean consigo los cuerpos que están orbitando en torno al cuerpo central o que están en caída libre hacia el mismo, de modo tal que podemos considerar que la curvatura del espacio-tiempo producida por el cuerpo central no es afectada de manera significativa por los cuerpos sobre los cuales ejerce su influencia el campo gravitacional del cuerpo central. De este modo, la masa-energía del cuerpo central (en este caso, el Sol) le dice al espacio-tiempo cómo se debe “curvear”, mientras que la curvatura de este espacio-tiempo le dice a los cuerpos sobre los cuales ejerece una influencia gravitatoria cómo se deben mover. Pero tratándose de dos cuerpos de masas del mismo orden de magnitud, la situación cambia y ya no es posible utilizar aproximaciones. Inclusive, ya ni siquiera podemos hablar de soluciones analíticas exactas, y el problema se complica de tal modo que se vuelve irresoluble por procedimientos manuales de cálculo. Afortunadamente, se pueden llevar a cabo simulaciones computarizadas para solventar nuestras limitaciones de cálculo manual, lo cual nos lleva al campo de la relatividad numérica. Pero aún con la ayuda de poderosas super-computadoras, los cálculos para problemas tan sencillos como el de dos cuerpos de masas iguales aproximándose (sin encontrarse directamente a lo largo de sus líneas de movimiento) puede terminar convirtiéndose en una tarea capaz de consumir varios días o inclusive semanas de super-cómputo continuo. Si en la mecánica Newtoniana el problema de los tres cuerpos es irresoluble por procedimientos matemáticos analíticos, en la mecánica relativista el problema de los dos cuerpos se vuelve irresoluble. Un ejemplo de un problema que involucra la interacción de dos campos gravitacionales que no se presta a un análisis sencillo es el del fenómeno de las mareas provocado por la atracción que ejerce la Luna sobre los mares de la Tierra:
En este caso, tenemos la interacción entre dos campos gravitacionales, el campo gravitacional de la Tierra que mantiene a los mares en el planeta, y el campo gravitacional de la Luna que “jala” a la masa de agua. Aunque estamos acostumbrados a hablar de una “atracción” gravitacional, en realidad tal atracción no existe porque la fuerza de atracción de la gravedad de Newton nunca existió. Lo único que existe, en la filosofía relativista, es la curvatura del espacio-tiempo que provocan la Tierra y la Luna en el 4-espacio intermedio que hay entre ambos cuerpos celestes, y esta curvatura no es algo que tenga una solución exacta como la que ofrece la métrica de Schwarzschild para un campo gravitacional simétricamente esférico y estático que no sea perturbado de modo significativo por los cuerpos a los que “atrae”. De cualquier modo, aún en la mecánica Newtoniana el análisis cuantitativo del fenómeno de las mareas usando números es un problema que no tiene solución exacta y tenemos que conformarnos con análisis de índole cualitativa o con simulaciones numéricas. Y si para llevar a cabo el análisis reemplazamos a la mecánica Newtoniana por la mecánica relativista, el problema se vuelve prácticamente irresoluble. Al igual que como ocurre en el estudio de fenómenos en los cuales las velocidades bajo consideración son considerablemente menores a la velocidad de la luz pudiéndose prescindir de la Teoría Especial de la Relatividad usando en su lugar la mecánica clásica no porque sea la correcta sino por su facilidad de uso, del mismo modo en el estudio de fenómenos en los que el campo gravitacional no es muy intenso se puede seguir utilizando la mecánica Newtoniana basada en su ley de gravitación universal que, aunque incorrecta, es mucho más sencilla de utilizar en una gran cantidad de problemas astronómicos, aunque eventualmente llega un momento en el que a la mecánica Newtoniana “se le acaba la gasolina” y no queda más opción que recurrir a la Relatividad General.