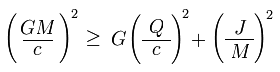Obsérvense los dos chorros emitidos en direcciones opuestas por el agujero negro. En la esquina superior derecha de la imagen tenemos una fotografía real tomada por el telescopio espacial Hubble de un agujero negro enorme que está situado en el centro de la galaxia NGC4261.
Existe la creencia generalizada de que el agujero negro estático, en caso de existir, no se produce tan fácilmente porque es el resultado del colapso de una estrella que se puede presumir que tenía algún movimiento de rotación similar al movimiento de rotación de la Tierra antes de colapsarse. Esta rotación implica la existencia de un movimiento angular J, mejor conocido como momento angular, el cual por el principio de la conservación de la cantidad de movimiento angular no se puede desvanecer hacia la nada sin dejar rastro, lo cual nos lleva a sospechar en la posibilidad de que el agujero negro creado por tal colapso gravitacional retiene dicha rotación, e inclusive en la posibilidad de que la solución matemática a tal agujero negro en rotación sea una solución exacta y no una aproximación. Este sería el agujero negro más realista de todos, este sería el que tendríamos mayores posibilidades de encontrar en el Universo. En 1963, el matemático neo-zelandés Roy Kerr logró resolver las ecuaciones de campo partiendo de la solución de Schwarzschild introduciendo el siguiente parámetro adicional de rotación:
a = J/M
que describe la rotación del agujero negro, el cual cuando toma el valor de cero se reduce a la descripción de un agujero negro estático sin rotación, siendo J la cantidad de movimiento angular del agujero negro en rotación y M el contenido total de masa-energía del mismo. La resolución del problema requirió recurrir a las coordenadas Boyer-Lindquist, las cuales son una generalización de las coordenadas usadas para la métrica del agujero negro de Schwarzschild.
La métrica Kerr que describe a un agujero negro en rotación es la siguiente:
en donde
ρ² = r² + a² cos θ
Δ = r² - 2Mr + a²
Δ = r² - 2Mr + a²
y (r, θ, φ) son las coordenadas polares usuales.
Obsérvese que si llevamos a cabo la expansión del quinto término (cuadrático) en la métrica de Kerr, obtenemos lo que se conoce como un término óblico, el término dtdφ. La aparición de este término en la métrica es responsable por lo que hoy se conoce como el efecto Lense-Thirring, con el cual los marcos de referencia cercanos al agujero negro en rotación son arrastrados junto con el mismo.
Esta característica interesante de que los agujeros negros en rotación sean capaces en la proximidad de su horizonte de evento de ir arrastando al espacio-tiempo la tenemos ilustrada en el siguiente graficado:
El “arrastre” producido por un agujero negro en rotación sobre el espacio-tiempo se puede visualizar mejor con el hundimiento del espacio-tiempo hacia la singularidad en el siguiente bosquejo:
El arrastre del espacio-tiempo en torno a la superficie de un agujero negro, similar al remolino que producen sobre el agua las aspas de una licuadora al ponerse en movimiento, es un efecto puramente relativista. Es imposible que esto pueda ocurrir en la mecánica clásica en donde el espacio absoluto, el tiempo absoluto y la atracción de la gravedad son cosas completamente independientes la una de la otra. Podemos definir una región afuera del horizonte de evento de los agujeros negros rotacionales conocida como la ergósfera o ergoesfera, una estructura de forma de forma elipsoidal coincidiendo su semieje menor con el eje de rotación de esta, achatándose en la dirección del eje de giro de manera similar a como lo hace la Tierra a causa de su rotación:
En la región de la ergósfera, el campo de gravedad del agujero negro rota junto con él arrastrando al espacio-tiempo. Dentro de la ergóesfera no existe el reposo, es imposible que un cuerpo no se mueva, pues el propio espacio gira en torno a la singularidad por lo que la materia que se encuentre en esa región rotará junto a ella. Dentro de la ergósfera, el espacio-tiempo es arrastrado en la dirección de la rotación del agujero negro a una velocidad mayor que la velocidad de la luz en relación con el resto del Universo. A causa de esto, los objetos dentro de la ergósfera no pueden permanecer estacionarios con respecto al resto del Universo a menos de que se estén moviendo a velocidades superiores a la velocidad de la luz, lo cual es imposible. Lo que sucede es que no son las partículas las que se estén moviendo con tal velocidad, es el espacio-tiempo de la ergósfera el que se mueve a velocidades superiores a la velocidad de la luz. Otra consecuencia del arrastre de los marcos de referencia es la existencia de energías negativas dentro de la ergósfera.
El límite exterior de la ergósfera es una superficie conocida como el límite estacionario. En este límite estacionario, los objetos que se estén moviendo a la velocidad de la luz permanecen estacionarios con respecto al resto del Universo, en virtud de que el espacio-tiempo justo en esta superficie límite está siendo arrastrado exactamente a la velocidad de la luz. Un poco fuera ya de este límite, el espacio-tiempo sigue siendo arrastrado, pero a una velocidad menor que la velocidad de la luz.
Puesto que la ergósfera está situada afuera del horizonte de evento, aún es posible que los objetos puedan escapar de la atracción gravitacional del agujero negro. De este modo, un objeto puede adquirir energía entrando en la ergósfera y tras esto escapar de la misma llevándose algo de la energía del agujero negro. En pocas palabras, el objeto puede salir con una mayor energía que la que tenía al entrar en la ergósfera. Esta posibilidad de extraer energía de un agujero negro en rotación fue propuesto por vez primera por el matemático Roger Penrose, y es conocido como el proceso Penrose. Teóricamente, la extracción máxima posible de energía de un agujero negro a través de su ergósfera es igual al 29% del total de la energía del agujero negro. Esta posibilidad de irle extrayendo a un agujero negro su energía a través de su ergósfera con la mira de aprovecharla para hacer un trabajo útil es precisamente lo que motivó el nombre de dicha región, derivado del griego ergon que significa “trabajo”. Sin embargo, no es posible estar extrayendo energía del agujero negro sin que ello tenga consecuencia alguna sobre el agujero negro. Al serle removida energía a través de su ergósfera, el agujero negro va disminuyendo su rotación, hasta que en un momento dado la ergósfera deja de existir habiendo dado el agujero negro todo lo que podía dar.
Un resultado interesante para el agujero negro tipo Kerr está dado por la fórmula que nos proporciona el área para el horizonte de evento de este tipo de agujero:
PROBLEMA: Si un agujero negro va perdiendo su rotación hasta detenerse por completo, ¿cuál será el área de su horizonte de evento de acuerdo con la ecuación de Kerr? ¿Está justificada esta conclusión?
Al perder un agujero negro su rotación, entonces J = 0 y el radical toma el valor de 1, con lo cual el área del horizonte de evento del agujero negro vendría siendo:
A = 16πG²M²/c4
Un agujero negro estático es esencialmente un agujero negro Schwarzschild con un horizonte de evento de radio rs = 2GM/c². La superficie esférica de su horizonte de evento será:
A = 4πrs² = 4π(2GM/c²)² = 16πG²M²/c4
Puesto que este resultado concuerda con el que obtuvimos a partir de la fórmula para el agujero negro de Kerr, entonces la conclusión dada por la fórmula de Kerr está justificada.
El interés que podamos tener en el área de la superficie de un agujero negro es propiciado por el siguiente esultado fundamental que es válido para cualquier tipo de agujero negro de la clase que sea:
Teorema del área: El área de la superficie del horizonte de evento de un agujero negro nunca puede disminuír. Después de cualquier proceso, el área sólo puede aumentar (o permanecer igual) con respecto al área inicial.
El teorema, expresado en terminología matemática, se puede escribir de la manera siguiente:
De acuerdo con el teorema, si dos agujeros negros se acercan y se fusionan bajo la influencia de su atracción gravitacional mutua, el área A del agujero negro resultante deberá ser mayor que las áreas A1 y A2 que tenían los dos agujeros negros antes de encontrarse:
A ≥ A1 + A2
El teorema del área será de enorme importancia cuando veamos la conexión que existe entre los agujeros negros y la segunda ley de la termodinámica.
Dos años después de conocerse la solución de Roy Kerr a las ecuaciones de campo, el matemático norteamericano Ezra Newman extendió la solución exacta encontrada por Roy Kerr para incluír agujeros negros en rotación que poseen una carga eléctrica denotada como Q.
Para que un agujero negro del tipo Kerr-Newman pueda ocurrir, debe cumplirse la siguiente condición esencial:
en donde M es la masa, Q es la carga y J es la cantidad del momento angular del agujero negro en rotación. Si se viola la desigualdad, aún es posible encontrar soluciones a las ecuaciones de campo para la familia de agujeros negros Kerr-Newman, pero estas soluciones nos describen singularidades “desnudas” en lugar de agujeros negros.
Habíamos visto anteriormente que cuando un agujero negro no es eléctricamente neutro, cuando tiene una carga eléctrica, encontramos que tenemos no uno sino dos horizontes separados, siendo uno de ellos el horizonte de evento usual y el otro un horizonte interno al horizonte de evento conocido como el horizonte de Cauchy. Tomando esto en cuenta, para el agujero negro más general de todos podemos definir tres superficies en torno a la singularidad situada en el centro, las cuales vistas “desde arriba” (la llamaremos una vista polar) son las siguientes.
y las cuales desde una perspectiva “ecuatorial” son las siguientes:
Resumiendo lo que hemos visto hasta ahora, existen cuatro soluciones matemáticas exactas a las ecuaciones de campo de la Teoría General de la Relatividad que permiten clasificar a los agujeros negros dentro de cuatro tipos posibles (posibles matemáticamente, físicamente la abundancia relativa que pueda haber de cada uno de ellos en el Universo es un tema propio de la filosofía de la astrofísica), dependiendo de que el agujero negro no tenga rotación alguna (J = 0) ó de que exhiba alguna rotación (J ≠ 0) y de que sea eléctricamente neutro (Q = 0) ó que posea alguna carga eléctrica (Q ≠ 0):