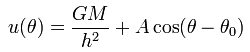Las tres leyes de Kepler
Primera Ley (1906): Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas, estando el Sol situado en uno de los focos.
Segunda Ley (1906): El radio vector que une el planeta y el Sol barre áreas iguales en tiempos iguales (de acuerdo con esta ley, el planeta orbitante en la figura de abajo se mueve más rápido del punto J al punto A que del punto D al punto E, siendo las áreas sombradas del segmento AJ y del segmento DE iguales) :
Tercera Ley (1906): Para cualquier planeta, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del Sol) es directamente proporcional al cubo de la distancia media con el Sol.
Kepler dedujo sus leyes a partir de observaciones astronómicas precisas obtenidas por Tycho Brahe, y aunque sabía que explicaban el movimiento planetario observado, no entendía las razones de este comportamiento.
En su libro conocido en castellano como “El sistema del mundo”, haciendo mención a la siguiente figura que aparece en su libro:
Newton se expresó de la siguiente manera al predecir por vez primera la posibilidad del hombre para poder crear satélites artificiales: “Si consideramos los movimientos de los proyectiles podremos entender fácilmente que los planetas pueden ser retenidos en ciertas órbitas mediante fuerzas centrípetras; pues una piedra proyectada se va apartando de su senda rectilínea por la presión de su propio peso y obligada a describir en el aire una curva, cuando en virtud de la sola proyección inicial habría debido continuar dicha senda recta, en vez de ser finalmente atraída al suelo; y cuanto mayor es la velocidad con la cual resulta ser proyectada más lejos llega, antes de caer a tierra. Podemos por eso suponer que la velocidad se incremente hasta que la piedra describa un arco de 1, 2, 5, 10, 100, 1000 millas antes de caer, de forma que al final, superando los límites de la Tierra, pasará al espacio sin tocarla... En la figura, se representa las curvas que un cuerpo describiría si fuese proyectado en dirección horizontal desde la cima de una alta montaña a más y más velocidad. Puesto que los movimientos celestes no son prácticamente retardados por la pequeña o nula resistencia de los espacios donde tienen lugar, supongamos, para conservar la analogía de los casos, que en la Tierra no hubiera aire, o al menos que éste está dotado de un poder de resistencia nulo o muy pequeño. Entonces, por la misma razón que un cuerpo proyectado con menos velocidad describe el arco menor y, proyectado con más velocidad, un arco mayor, al aumentar la velocidad, terminará por llegar bastante más allá de la circunferencia de la Tierra, retornando a la montaña desde la que fue proyectada. Y puesto que las áreas descritas por el movimiento del radio trazado desde el centro de la Tierra son proporcionales a su tiempo de descripción, su velocidad al retornar a la montaña no será menor que al principio, por lo que reteniendo la misma velocidad, describirá la misma curva una y otra vez, obedeciendo a la misma ley”.
Antes de entrar en el estudio de las orbitas planetarias desde el punto de vista de la Relatividad General, haremos un repaso sobre cómo es posible obtener las leyes de Kepler a partir de la ley de la gravitación universal de Newton.
Clásicamente, para el análisis del movimiento de un cuerpo que siempre se está moviendo bajo la influencia de una fuerza que siempre está dirigida hacia un punto central, se recurre al uso de coordenadas polares con el origen de las mismas coincidiendo con el centro de la fuerza, dejando abierta la posibilidad de que la órbita pueda ser circular o elíptica. En coordenadas polares, la componente radial de una aceleración es:
y la componente transversal (angular) de la aceleración es:
Puesto que la fuerza es completamente radial por estar dirigida hacia el centro de atracción que coincide con el origen del sistema de coordenadas, se concluye que la aceleración transversal debe ser cero, o sea aθ = 0, con lo cual:
Integrando la expresión:
Este es precisamente el enunciado matemático de la segunda ley de Kepler, que nos dice que la línea imaginaria que une a un planeta con el Sol barre áreas iguales en tiempos iguales. La constante de integración resulta ser h, el momento angular L del planeta por unidad de masa M. Entonces:
Aquí se ha introducido, siguiendo la costumbre usual, la variable auxiliar:
La fuerza radial f(r) por unidad de masa debe ser igual a la aceleración radial que se ha definido arriba, de acuerdo con la segunda ley de Newton F = ma. Resolviendo la ecuación diferencial de arriba con respecto al tiempo nos dá:
Aquí es precisamente en donde entra en acción la ley de la gravitación universal de Newton que nos dice que la fuerza de atracción gravitatoria entre dos cuerpos es igual a la inversa del cuadrado de la distancia que separa dichos cuerpos. Entonces (la masa m del planeta orbitante no aparece explícitamente porque la fuerza ha sido designada como la fuerza por unidad de masa):
siendo G la constante de gravitación universal y M la masa del cuerpo central que en este caso es el Sol. Substituyendo en la ecuación anterior obtenemos lo siguiente:
Obsérvese que el lado derecho de la ecuación es igual a una constante, en virtud de que la G, M y h son constantes (la constancia de h deviene del principio de la conservación del momento angular). De este modo, para una fuerza de carácter gravitacional, o en general para cualquier fuerza cuya magnitud disminuya en razón inversa del cuadrado de la distancia, el lado derecho de la ecuación será una constante fija. Resolviendo esta ecuación diferencial obtenemos la siguiente solución:
en donde A y θ0 = son constantes arbitrarias que nos resultan de la integración.
La ecuación para la órbita descrita por la partícula (o el planeta) es entonces:
en donde e está definida como:
Esta es una solución que puede ser reconocida como la ecuación de una sección cónica expresada en coordenadas polares (r,θ). Aquí podemos hacer la siguiente identificación:
Para el caso que nos ocupa, tratándose de una trayectoria cerrada ésta debe ser una trayectoria elíptica, con el centro de la fuerza ocupando uno de los focos de la elipse. Este es precisamente el enunciado matemático de la primera ley de Kepler.
Pero en la Relatividad General, la fuerza de la gravedad deja de existir, llevándose consigo a los museos a la ley de la gravitación universal de Newton. Ahora todo se explica en base a la curvatura del espacio-tiempo. Ya hemos visto que la presencia de toda masa-energía ocasiona una curvatura cuatri-dimensional en lo que de otras maneras sería un espacio-tiempo plano, capaz de desviar la trayectoria de un rayo de luz o de un cuerpo material que pase cerca de dicho cuerpo. Pero la curvatura cuatri-dimensional que puede ocasionar una masa-energía no sólo es capaz de “pandear” el espacio-tiempo en torno a ella en una forma capaz de desviar la trayectoria de los cuerpos que pasan cerca de ella como ocurre con los cometas que pasan cerca del Sol. La curvatura puede ser tal que inclusive el espacio-tiempo es capaz de cerrarse sobre sí mismo:
Un espacio-tiempo cerrado sobre sí mismo como el que vemos arriba en la figura de la derecha representa una superficie en la cual el potencial gravitacional Newtoniano clásico tiene el mismo valor. Una superficie tal es precisamente la que recorren los cuerpos en órbita como ocurre con la Luna girando en torno a la Tierra o los planetas girando en torno al Sol, si tienen la suficiente energía cinética para poder mantenerse viajando sobre dicha superficie. Y como debe ser obvio, bajo el concepto relativista de la curvatura del espacio-tiempo la fuerza de atracción universal entre dos cuerpos propuesta por Newton no existe, no hay fuerza de atracción tal, todo lo que hay son curvaturas en el espacio-tiempo 4-dimensional del Universo.
El problema fundamental con el nuevo esquema es que inclusive con dos cuerpos de masas diferentes aproximándose el uno al otro no necesariamente compartiendo un mismo plano de movimiento es que cada uno de ellos introduce su propia curvatura en el espacio-tiempo del Universo, y la interacción entre ambas curvaturas del espacio-tiempo conforme se van desplazando al irse aproximando los cuerpos que originan dichas curvaturas se convierte en un problema de difícil solución matemática excepto para casos especiales (como el caso de dos cuerpos de la misma masa orbitando como un sistema binario como si fuesen los extremos de una mancuerna girando libremente sobre su eje de rotación así como los demás casos que involucren algún tipo de simetría), el cual de hecho no tiene solución matemática exacta de carácter general, y frecuentemente es necesario recurrir a simulaciones computarizadas a partir de condiciones iniciales muy específicas para poder resolver un problema. Si en el esquema propuesto por Newton excepto para casos especiales la interacción gravitacional entre tres cuerpos era matemáticamente irresoluble (este es el problema conocido como el problema de los tres cuerpos) dando lugar a comportamientos como el que se muestra en el siguiente diagrama (la trayectoria de cada uno de los tres cuerpos está dibujada en color diferente) que son precisamente los que dan origen a la teoría del caos:
en el esquema propuesto por Einstein la interacción entre dos curvaturas del espacio-tiempo no necesariamente iguales (producidas por cuerpos con la misma masa) conforme se van aproximando los cuerpos se vuelve insoluble por procedimientos analíticos exactos. La única forma en la cual se puede resolver un problema analíticamente sin el beneficio de una computadora es recurriendo a aproximaciones.
En el caso del sistema solar, la primera aproximación obvia consiste en suponer que, debido a que la masa del Sol es mucho mayor que la masa de cualquiera de los planetas que giran en torno suyo (lo cual equivale a decir que la gravedad de cada uno de los planetas no tiene efectos significativos sobre el mismo Sol permitiendo anclar al Sol como un centro inamovible), la única curvatura apreciable en el espacio-tiempo del sistema solar es la introducida por el mismo Sol; del mismo modo en que podemos suponer que la curvatura producida en el espacio-tiempo en torno a la Tierra por los satélites artificiales lanzados por el hombre es mucho menos que la curvatura en el espacio-tiempo producida por la misma Tierra con la cual mantiene a sus satélites girando en torno suyo. Este tipo de aproximación fue precisamente lo que Einstein llevó a cabo cuando descubrió un efecto imposible de ser predicho por Newton para un sistema solar consistente en un solo sol y en un solo planeta: la precesión de las órbitas del planeta Mercurio que está girando en torno al sol. Las órbitas predichas de acuerdo con la ley de la gravitación universal de Newton son órbitas perfectamente elípticas por toda la eternidad, con la elipse orbitan manteniéndose exactamente en el mismo lugar por siempre. Esta es una situación en la cual las ecuaciones del movimiento planetario de la Relatividad General no pueden ser simplificadas para aproximar una predicción de por sí ausente en la mecánica celestial Newtoniana. Aquí no se puede llevar a cabo ninguna reducción a un límite clásico que no existe. La única forma bajo el esquema de Newton de producir una precesión en la órbita de un planeta que esté girando en torno a una estrella es introducir un segundo planeta que influya gravitacionalmente en el otro planeta. Bajo el esquema de Newton, tal cosa ocurre por sí sola sin la necesidad de introducir planetas adicionales.
Todos los planetas girando en torno al Sol tendrán una precesión en sus órbitas de acuerdo a la Relatividad General. Sin embargo, estos efectos sólo adquieren importancia tratándose de planetas como Mercurio que estén lo suficientemente cerca del Sol como para que los efectos relativistas puedan salir a relucir.
En la Relatividad General, suponiendo que tenemos un cuerpo central de masa M al cual consideramos fijo, la ecuación de movimiento relativista planetario para una partícula de prueba resulta estar dada por la fórmula:
en donde:
α = 3μ/c²
μ = GM
μ = GM
y los demás símbolos son como los que se han definido previamente.
La derivación de la ecuación de movimiento relativista, como el lector posiblemente lo sospecha ya, se hace a partir de la métrica sin recurrir a ninguna “fuerza de gravedad”, empleando para ello una métrica apropiada que describa una solución con simetría esférica a las ecuaciones de campo de Einstein, siendo la métrica de Schwarzschild una de las más utilizadas para tal efecto. El lector debería tomar una pausa para comparar la ecuación de movimiento planetario relativista con la ecuación de movimiento planetario clásico.
A continuación llevaremos a cabo la derivación de un efecto relativista relacionado con las órbitas planetarias: la precesión anómala de los planetas en sus órbitas en torno al Sol. Y lo haremos en una forma muy parecida a como lo hizo Einstein en su tiempo, sin contar con el beneficio de la solución exacta de Schwarzschild, recurriendo obviamente a aproximaciones.
En principio, todos los planetas del sistema solar poseen una precesión lenta de sus órbitas que impide que dichas órbitas sean perfectamente elípticas. En parte, esta precesión de las órbitas puede ser explicada con la mecánica Newtoniana mediante la influencia gravitacional causada por la presencia de los otros planetas del sistema solar. Pero en el caso de Mercurio, el planeta más cercano al Sol, la precesión es mayor de una manera que no puede ser explicada recurriendo a las fórmulas de Newton.
La solución aproximada encontrada por Einstein en 1915 difiere en el componente grr de la métrica “diagonal” especificada por la solución exacta dada por Karl Schwarzschild para un campo esféricamente simétrico:
ds² = gtt dt² + grr dr² + gθθ dθ + gφφ dφ²
ds² = (1 - 2GM/rc²) dt² + [1 - 2GM/rc²] -1 dr² + r² dθ + r² sen² θ dφ²
por el factor q = 1-(2GM/rc²) de la manera siguiente:
Como ya se ha dicho y se volverá a repetir aquí, todo el secreto de las soluciones a las ecuaciones de campo de la Relatividad General está en la métrica que se utilice, todo deriva de la métrica. Schwarzschild encontró una métrica exacta, pero Einstein sin contar con la solución exacta decidió probar su suerte sin tomar en cuenta el factor q. El error que se comete equivale a una diferencia de segundo orden para 2GM/rc². Usando su métrica aproximada para un campo en el vacío esféricamente simétrico, Einstein hizo algo que se puede hacer de inmediato cuando se tiene una métrica a la mano: evaluó los símbolos de Christoffel; tras lo cual dió el siguiente paso que se puede hacer una vez que se tiene a los símbolos de Christoffel a la mano: escribió las ecuaciones geodésicas del movimiento. De este modo llegó directamente (tal y como se acostumbra hacerlo en libros de texto contemporáneos) a la siguiente ecuación:
en donde x = 1/r es la inversa de la distancia radial al Sol, φ es la coordenada angular del plano de la órbita, los símbolos A y B son constantes de integración (B resulta ser el momento angular y A es una cantidad relacionada con la energía del cuerpo en órbita) y α = 2M en donde M es la masa del Sol en unidades geometrizadas. Si utilizamos la métrica exacta de Schwarzschild, esta ecuación sería exacta con q = 1, pero con la métrica aproximada de Einstein el valor de q viene siendo 1 - α²x². Dividiendo entre q, o lo que viene siendo lo mismo, multiplicando por 1 + α²x², la ecuación basada en la métrica aproximada de Einstein resulta ser:
Afortunadamente, Einstein reconoció que podía hacer q = 1 sin afectar el resultado Newtoniano de orden más bajo (o sea, el efecto más significativo), de modo tal que procedió a utilizar directamente la ecuación:
que es precisamente la ecuación correcta y exacta, aunque Einstein creía que era tan solo una aproximación. A partir de este punto, la mayoría de las demostraciones modernas llevan a cabo una diferenciación de esta ecuación con respecto a φ, lo cual nos produce una ecuación “harmónica” de segundo orden de la cual se puede inferir la precesión relativista del perihelio del planeta. Sin embargo, Einstein en lugar de hacer esto tomó la raíz cuadrada de la inversa de ambos lados de la ecuación, produciéndose con ello la integral elíptica del desplazamiento angular entre los dos parámetros radiales inversos extremos x1 y x2 (al decir extremos, nos estamos refiriendo al apogeo, la distancia a la cual el cuerpo en órbita se encuentra más alejado, y al perigeo, la distancia a la cual el cuerpo en órbita se encuentra más cercano, aunque tratándose del Sol las palabras correctas vendrían siendo afelio y perihelio):
Y por cierto, en caso de que llevásemos a cabo la integración sobre la distancia radial r en lugar de llevarla a cabo sobre la distancia radial inversa x, obtendríamos un factor de r² en el denominador, en virtud de que dx = -dr/r².
Determinar una solución explícita exacta en términos de funciones elementales para la integral elípítica que tenemos arriba no es algo que generalmente se pueda llevar a cabo, de modo tal que esta vía de solución no se antoja muy factible. De cualquier modo, Einstein pudo aproximar a la integral elíptica con el grado de precisión requerido. Para lograrlo, hizo uso del hecho de que los límites de la integración, x1 y x2, representan los recíprocos de las distancias del afelio y del perihelio en donde la derivada de r con respecto a φ se desvanece. Por lo tanto, tenemos que integrar entre dos cúbicas bajo el signo del radical. Tal y como lo hizo Einstein en su papel original, designaremos a estas dos raíces α1 y α2. Designaremos también como α3 a la tercera raíz, de modo tal que podemos escribir el polinomioque está bajo el signo de la raíz cuadrada de la manera siguiente:
Puesto que el coeficiente de x² en el polinomio mónico en el lado izquierdo es 1/α, tenemos entonces:
De este modo, el producto de α y de α3 se puede expresar de la manera siguiente:
Más aún, notando que las cantidades αx, αα1 y αα2 son extremadamente pequeñas en comparación con la unidad (esto viene del hecho de que cada una de ellas es aproximadamente igual al doble de la masa solar en unidades geometrizadas, que viene siendo una cantidad un poco menor que 1.5 kilómetros, divida entre el radio de la órbita de Mercurio, que es de aproximadamente 55 millones de kilómetros), podemos ver que el denominador 1 - αx en el segundo factor representa una corrección del orden de (αx)² al factor total, de modo tal que se puede considerar despreciable. De este modo, sin pérdida considerable de precisión, podemos escribir:
α(x - α3) ≈ (αx - 1) [1 - α(α1 + α2)]
y por lo tanto la integral elíptica se puede escribir de la siguiente manera:
Haciendo uso de la aproximación (1 - z) -1/2 ≈ 1 + z/2 para valores pequeños de z, podemos sacar el factor constante fuera de la integral, y subir el factor final, de modo tal que la integral se puede escribir del modo siguiente:
Esta es una integral analítica, que puede ser evaluada en forma cerrada, dando como resultado:
Esta es la distancia angular del arco del apogeo (afelio) al siguiente perigeo (perihelio), de modo tal que la longitud total del arco de un ciclo completo de un perigeo (perihelio) al siguiente es el doble de esta cantidad, y si substraemos 2π obtenemos la precesión por ciclo. Esta es precisamente la precesión relativista que tan afanosamente estaba buscando Einstein. El tercer término es despreciable, de modo que tenemos el siguiente resultado:
en donde L es el semi-latus rectum de la elipse de la órbita. Metiendo valores para la masa M del Sol en unidades geometrizadas (1.475 kilómetros) y el semi-latus rectum para la órbita de Mercurio en torno al Sol que es 55.4430 millones de kilómetros, esto nos dá 0.1034 arcos de segundo por revolución, y puesto que Mercurio acumula un total de 414.9378 revoluciones en torno al Sol por siglo, esto nos dá 42.9195 segundos de arco por siglo, lo cual concuerda de modo excelente con las observaciones astronómicas. Este fue el primer gran triunfo de la Relatividad General, pudiendo aclarar algo que la mecánica Newtoniana simple y sencillamente era incapaz de explicar.
La demostración llevada a cabo parecería depender de un conocimiento previo de la integral indefinida:
pero hay que tomar en cuenta que la expresión del lado derecho (la que se obtiene tras llevarse a cabo la integración) se simplifica considerablemente con la substitución de b o c por la variable x, porque para cualquiera de estos dos argumentos el segundo término se desvanece, y el primer término se reduce a lo siguiente:
Por lo tanto, la integral definida de x = b a x = c es simplemente:
Podemos ver que en el caso a = 0 la integral definida es simplemente igual a π. Este es un resultado tan elegante que muy posiblemente formaba parte ya del curriculum escolar de materias al finalizar el siglo XIX, y es muy posible que Einstein (o Michele Besso o Marcel Grossman, los dos colegas matemáticos de Einstein siempre disponibles para proporcionarle ayuda) haya tenido conocimiento acerca de esta integral definida. Por otro lado, no es muy difícil evaluar esta integral directamente si llevamos a cabo un cambio de variables a la variable ω en base a la siguiente relación:
La variable x cambia de b a c conforme la variable ω cambia de - π/2 a + π/2. Tomando diferenciales, de esta misma expresión obtenemos lo siguiente:
La substitución de esto último en la integral definida nos dá:
La integral de un término seno es un término coseno, que termina dando los mismos valores para los límites ω = ± π/2, de modo tal que esto se desvanece dejándonos únicamente con la ecuación:
Una discusión sobre la explicación relativista de la precesión anómala de Mercurio en torno al Sol utilizando la métrica exacta de Schwarzschild deberá esperar a que se cubra el tema de la solución de Schwarzschild, lo cual se llevará a cabo posteriormente.