El concepto de que la energía no se crea ni se destruye, de que la energía no puede salir de la nada, es un concepto tan esencial en el estudio de la Naturaleza que ni siquiera Einstein se atrevió a modificarlo en lo más mínimo. De este modo, tanto en la mecánica clásica como en la mecánica relativística, el principio de la conservación de la energía en una de sus formulaciones nos dice que la energía cinética K adquirida por un cuerpo debe ser igual al trabajo hecho por una fuerza externa F al aumentar la velocidad del cuerpo desde cero hasta un valor u. Por definición:
K = ∫F·ds
Para un movimiento unidimensional que se lleva a cabo a lo largo del eje-x:
K = ∫0 u Fdx
La fuerza relativística F está dada por el cambio del momentum relativístico P = γm0u con respecto al tiempo (siendo m0 la masa en reposo del cuerpo, la cual es una constante), de tal modo que:
K = ∫0 u [d/dt(γm0u)] dx
K = ∫0 u [d(γm0u)] [dx/dt]
K = ∫0 u [d(γm0u)] [u]
K = ∫0 u u·d(γm0u)
K = ∫0 u [d(γm0u)] [u]
K = ∫0 u u·d(γm0u)
En el factor de corrección γ es importante reemplazar la velocidad constante V por la velocidad variable u ya que como resultado de la aplicación de la fuerza F la velocidad del cuerpo estará aumentando constantemente:
γ = 1 / √1 - u²/c²
Tomando diferenciales de la cantidad γm0u usando la regla d(uv) = udv + vdu:
d(γm0u) = m0γdu + m0udγ
De acuerdo al cálculo infinitesimal, la diferencial dγ es igual a:
dγ = d (1 /√1 - u²/c²)
dγ = d {1 - u²/c²}-½
dγ = (u/c²) {1 - u²/c²}-3/2 du
dγ = d {1 - u²/c²}-½
dγ = (u/c²) {1 - u²/c²}-3/2 du
Con esto, la diferencial d(γm0u) resulta ser:
d(γm0u) = m0 [ {1 - u²/c²}-½ du + (u/c²) {1 - u²/c²}-3/2 du ]
Simplificando con un poco de álgebra, esto se reduce a:
d(γm0u) = m0 {1 - u²/c²}-3/2 du
Con esto, regresando a la expresión original de la energía cinética K:
K = ∫0 u u·d(γm0u)
K = ∫0 u u·{m0 {1 - u²/c²}-3/2 du)}
K = m0 ∫0 u { {1 - u²/c²}-3/2 u du)}
K = ∫0 u u·{m0 {1 - u²/c²}-3/2 du)}
K = m0 ∫0 u { {1 - u²/c²}-3/2 u du)}
Llevando a cabo la integración y tomando los límites:
K = m0c² [ (1 - u²/c²)}-½ - 1 ]
K = γm0c² - m0c²
K = γm0c² - m0c²
Este resultado nos dice que la energía cinética K de un cuerpo representa la diferencia entre lo que llamaremos la energía total E de la partícula en movimiento y la energía en reposo E0 de la partícula precisamente cuando la partícula está en reposo.
K = E - E0
en donde:
E = γm0c²
E0 = m0c²
E0 = m0c²
La conclusión que hemos dado a las definiciones anteriores es correcta ya que si la velocidad del cuerpo es cero, entonces V/c también es igual a cero y el factor γ = 1, con lo cual tendríamos que E = m0c² y por lo tanto K = 0, o sea una energía cinética de cero (un cuerpo en reposo no tiene energía de movimiento, su energía cinética K es cero). Habiendo definido la energía en reposo que posee el cuerpo cuando no se está moviendo ante nosotros de modo tal que
E0 = m0c²
nos vemos obligados a concluír que la masa de todo cuerpo en reposo equivale a cierta cantidad de energía dada por la ecuación anterior, la materia y la energía son dos cosas completamente equivalentes, son dos manifestaciones distintas de lo mismo. Así como los conceptos independientes del espacio y del tiempo fueron fusionados en un solo concepto único e indivisible bajo una sola palabra, el espacio-tiempo, también la masa y la energía han sido fusionadas como una sola cosa. Esta es indudablemente la conclusión más conocida de Einstein, su fórmula más famosa, obtenida completamente dentro del marco de la Teoría Especial de la Relatividad.
Toda cantidad limitada de materia es equivalente a cierta cantidad limitada de energía, y viceversa. Y resulta que una cantidad muy pequeña de materia es equivalente a una cantidad enorme de energía.
PROBLEMA: Verificar que la expresión relativista para la energía cinética de un cuerpo se reduce a la expresión clásica para velocidades suficientemente bajas en comparación con la velocidad de la luz.
Clásicamente, la energía cinética de un cuerpo está dada por la expresión:
K = ½ mv²
Para velocidades bajas en comparación con la velocidad de la luz, podemos recurrir al teorema del binomio para expandir el primer término en el lado derecho de la igualdad de la expresion
K = γm0c² - m0c²
K = (1 /√1 - u²/c²) m0c² - m0c²
K = {1 - u²/c²}-½ m0c² - m0c²
K = {1 + (½) (u²/c²) + ...} m0c² - m0c²
K = (1 /√1 - u²/c²) m0c² - m0c²
K = {1 - u²/c²}-½ m0c² - m0c²
K = {1 + (½) (u²/c²) + ...} m0c² - m0c²
Ignorando los términos de orden superior, tenemos que la expresión relativista se nos reduce a:
K = m0c² + (½) (u²/c²) m0c² - m0c²
K = ½ m0u²
K = ½ m0u²
lo cual está en acuerdo con la expresión clásica.
Una forma común de abreviar la expresión para la energía cinética relativista K, fácil de recordar, es la siguiente:
K = (γ - 1) m0c²
Sin embargo, esta expresión resumida no muestra en forma explícita la relación que hay entre la energía cinética relativista K, la energía total E y la energía en reposo, y debe ser considerada más bien como una ayuda mnemotécnica en la resolución de problemas.
PROBLEMA: Si la energía en reposo de un gramo de agua pudiera ser transformada completamente en energía, ¿cuánta agua podría ser calentada desde los cero grados centígrados (el punto de congelación del agua) hasta los cien grados centígrados (el punto de ebullición del agua)? Tómese 1 caloría = 4.19 joules.
Los cálculos serán llevados a cabo bajo el sistema MKS de unidades. Un gramo de agua es igual a una milésima de kilogramo, con lo cual la energía en reposo de un gramo de agua es igual a:
E0 = m0c²
E = (0.001 Kg) (3·108 metros/segundo)
E = 9·1013 Kg·metro²/segundo²
E = 9·1013 joules
E = 2.14·1013 calorías
E = (0.001 Kg) (3·108 metros/segundo)
E = 9·1013 Kg·metro²/segundo²
E = 9·1013 joules
E = 2.14·1013 calorías
Por la misma definición de lo que es una caloría, la capacidad calorífica del agua;
C = ΔQ/mΔT
es igual a la cantidad de calor requerida para elevar la temperatura de un gramo de agua en un grado centígrado, o sea C = 1 caloría/gramo·°C.
Si el calor ΔQ proviene de la energía en reposo E de un gramo de agua, entonces:
m = ΔQ/CΔT = E/CΔT
m = E/CΔT
m = (2.14·1013 calorías)/(1 caloría/gramo·°C)(100 °C)
m = 2.14·1011 gramos = 2.14·1011 Kg
m = 214,000,000 Kg.
m = E/CΔT
m = (2.14·1013 calorías)/(1 caloría/gramo·°C)(100 °C)
m = 2.14·1011 gramos = 2.14·1011 Kg
m = 214,000,000 Kg.
Podríamos calentar 214 mil toneladas de agua llevándolas desde su punto de su punto de congelación hasta su punto de ebullición con tan sólo la energía que podríamos obtener convirtiendo la masa de un gramo de agua en energía.
La enorme cantidad de energía que podemos obtener de una cantidad tan pequeña de materia es precisamente el medio mediante el cual nuestra propia estrella el Sol nos puede proporcionar diariamente abundantes cantidades de energía que hacen posible la vida en la Tierra. Cada día somos testigos de una de las confirmaciones más espectaculares de la Teoría Especial de la Relatividad.
PROBLEMA: Un electrón es acelerado en un ciclotrón hasta alcanzar una energía cinética K de 2 GeV (= 109 eV). ¿Cuál es la relación entre la masa del electrón que ha sido acelerado y su masa en reposo?
La relación entre la masa m del electrón que ha sido acelerado y su masa en reposo m0 se puede expresar como m/m0 o bien mc²/m0c². Tenemos además lo siguiente:
E = K + E0
mc² = K + m0c²
mc² = K + m0c²
Entonces:
m/m0 = mc²/m0c² = (K + m0c²) /m0c² = (2·109 eV + 0.511·106 eV) / 0.511 MeV
m/m0 = 3,914
m/m0 = 3,914
De este modo, una vez acelerado por el ciclotrón, el electrón se comporta como si tuviera una masa casi 4 mil veces mayor que la que tiene cuando está en reposo. Sin embargo, esta no es una masa real en el sentido de que el electrón haya aumentado su masa propia. Lo que sucede es que la energía que le ha sido impresa hace que experimentalmente se comporte como si tuvierse una masa mucho mayor que la que realmente tiene, en virtud de la equivalencia que hay entre la masa y la energía.
Lo que acabamos de obtener nos permite analizar los procesos de índole atómica o sub-atómica en los cuales por la desintegración de un átomo tengamos dos o más partículas resultantes cuyas masas sumadas no sean iguales a la masa del átomo original (lo que llamamos un defecto de masa) nos indica que, al no haber desaparecido dicha masa hacia la nada, necesariamente tuvo que haber sido convertida dicha masa ausente en energía pura, ya que el principio de la conservación de la energía sigue siendo completamente válido inclusive dentro de la Teoría de la Relatividad.
Antes de continuar, definiremos una unidad ampliamente utilizada en la resolución de problemas de índole atómica y sub-atómica, el electron-voltio simbolizado como eV. Es la energía E adquirida por la carga q de un electrón cuando es acelerado por una diferencia ΔV de potencial eléctrico de un voltio, bajo la fórmula E = qΔV, aplicándosele las mismas convenciones del sistema de unidades MKS, de modo tal que MeV representa una energía medida en millones de electron-voltios. Puesto que la carga de un electrón es igual a 1.6·10-19 coulombs en el sistema MKS de unidades, tenemos entonces el siguiente factor de conversión:
1 eV = (1.6·10-19 coulombs) · (1 volt) = 1.6·10-19 joule
PROBLEMA: ¿Cuál es la energía en reposo de un electrón, sabiendo que su masa en reposo el sistema MKS es de 9.1·10-31 Kg? Dar la respuesta tanto en joules como en MeV.
Este problema tiene una resolución directa:
E0 = m0c²
E0 = (9.1·10-31 Kg) (3·10-8 metros/seg)²
E0 = 8.19 10-14 joules
E0 = (9.1·10-31 Kg) (3·10-8 metros/seg)²
E0 = 8.19 10-14 joules
E0 = (8.19 10-14 joules) (1 eV /1.6·10-19 joule) (1 MeV / 106 eV)
E0 = 0.511 MeV
La energía en reposo dentro de la Teoría de la Relatividad es una forma nueva de proporcionar la masa en reposo de una partícula, lo cual tiene sus ventajas en estudios de física atómica y nuclear, como lo demuestra lo que veremos a continuación.
PROBLEMA: La energía en reposo de un protón es de 938.256 MeV, y la energía en reposo de un neutrón es de 939.550 MeV. Si la energía en reposo de un deuterón (una partícula nuclear formada por un protón y un neutrón unidos el uno al otro) es de 1875.580 MeV, ¿es factible esperar que el deuterón se pueda fisionar por sí solo descomponiéndose en sus partes elementales?
Sumando las energías en reposo del protón y el neutrón:
938.26 MeV + 939.55 MeV = 1877.81 MeV
encontramos que, por una diferencia pequeña, las energías en reposo de ambas partículas tomadas independientemente es mayor que la energía en reposo del deuterón, y por lo tanto el deuterón no se puede fisionar por sí solo. Se requiere suministrarle una energía al deuterón para provocar tal fisión, ya que la energía del enlace es:
1877.81 MeV - 1875.58 MeV = 2.23 MeV
Esta energía necesaria para romper el enlace puede ser suministrada ya sea bombardeando al deuterón con una partícula energética o con radiación electromagnética. Del mismo modo, cuando se forma un deuterón, se libera una cantidad de energía igual a los 2.23 MeV que serían necesarios para volver a descomponerlo en sus partes esenciales.
PROBLEMA: ¿Cuál es la velocidad adquirida por un electrón que es acelerado a través de una diferencia de potencial de 100 mil voltios?
La energía cinética (no la energía total que incluye la masa en reposo) adquirida por un electrón bajo una diferencia de potencial de 100 mil voltios es igual a K = qΔV = (1 electrón)(100 mil voltios) = 100 KeV. Entonces, empleando la relación relativista:
K = γm0c² - m0c²
K = (γ - 1) m0c²
K = (γ - 1) m0c²
La masa en reposo del electrón ya la obtuvimos en un problema previo, es de 0.511 MeV. Por lo tanto:
100 KeV = (γ - 1) (0.511 MeV)
γ - 1 = 0.1957
γ = 1.1957
1 / √1 - u²/c² = 1.1957
γ - 1 = 0.1957
γ = 1.1957
1 / √1 - u²/c² = 1.1957
u = 0.548c
PROBLEMA: Un mesón K0 en reposo decae en dos mesones π0:
K0 → π0 + π0
Si la energía en reposo del mesón K0 es de 498 MeV y la energía en reposo del mesón π0 es de 135 MeV, ¿cuál será la energía cinética K de cada mesón π0 suponiendo que toda la energía que resulta del decaimiento del mesón K0 será portada como energía cinética por ambas partículas π0 resultantes del decaimiento?
Si la energía en reposo de cada mesón π0 es de 135 MeV, entonces la energía en reposo de dos de dichas partículas será de 270 MeV, una diferencia de 228 MeV con respecto a la energía en reposo de 498 MeV del mesón K0. Por el principio de la conservación de la energía, la energía total inicial Einicial que es igual a la energía en reposo del mesón K0 debe ser igual a la energía en reposo de cada mesón π0 más la energía cinética K con la que sale disparado cada mesón en sentido contrario:
Einicial = Efinal
Einicial = (m2c² + K) + (m2c² + K)
Einicial = 2m2c² + 2K
498 MeV = 2 (135 MeV) + 2K
K = 114 MeV
Einicial = (m2c² + K) + (m2c² + K)
Einicial = 2m2c² + 2K
498 MeV = 2 (135 MeV) + 2K
K = 114 MeV
En el problema anterior, toda la energía aparentemente perdida termina siendo convertida en la energía cinética de las dos partículas resultantes.
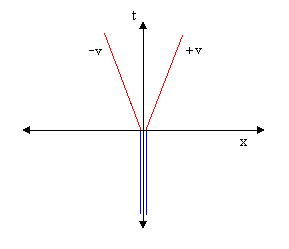
El diagrama espacio-tiempo para lo que acabamos de ver tendrá el siguiente aspecto en el cual una línea del mundo única para una sola partícula se rompe en dos líneas del mundo diferentes para dos partículas diferentes, una moviéndose en un sentido (hacia la derecha, en la dirección +x) y la otra moviéndose en el sentido contrario (hacia la izquierda, en la dirección -x):
PROBLEMA: Un cuerpo en reposo se rompe espontáneamente en dos partes que se mueven en sentidos opuestos. Las masas en reposo y las velocidades de las partes son m1 = 3 Kg a u1 = 0.8c y m2 = 5.33 Kg a u2 = 0.6c. Hallar la masa en reposo del cuerpo original.
Por el principio de la conservación de la energía:
Einicial = Efinal
La energía inicial es la del cuerpo que estaba en reposo, siendo ésta Einicial = mc². Las energías totales de las dos partes en las que se rompe el cuerpo están dadas E1 = γ1m1c² y E2 = γ2m2c²:
Entonces tenemos lo siguiente:
mc² = γ1m1c² + γ2m2c²
m = (√1 - u1²/c²) m1 + (√1 - u2²/c²) m2
m = (3 Kg / √1 - 0.64) + (5.33 Kg / √1 - 0.36)
m = 11.66 Kg
m = (√1 - u1²/c²) m1 + (√1 - u2²/c²) m2
m = (3 Kg / √1 - 0.64) + (5.33 Kg / √1 - 0.36)
m = 11.66 Kg
Así, al empezar teníamos una masa total de 11.66 Kg, y después de la desintegración terminamos con una masa total de 8.33 Kg. En la Teoría de la Relatividad no hay un principio de “conservación de la masa”. Lo que hay es un principio de conservación de la masa-energía.
Habiendo visto procesos de desintegración, veamos ahora procesos relativistas que involucran colisiones en las cuales dos cuerpos quedan trabados después del choque:
El análisis que llevaremos a cabo es completamente válido aunque el cuerpo absorbido no sea un cuerpo material sino un fotón de luz, como lo veremos en el siguiente problema.
PROBLEMA: Se pueden presentar argumentos para demostrar que un fotón no puede ser absorbido por un electrón libre. Sin embargo, puede ser absorbido por un electrón estacionario en la vecindad de un núcleo pesado. Si un fotón con una energía de 1 MeV choca con un electrón estacionario en la vecindad de un núcleo pesado, y si despreciamos la energía de retroceso del núcleo, ¿cuál será la velocidad del electrón después del choque al ser sacado fuera del átomo?
Apelamos nuevamente al principio de la conservación de la energía antes y después del choque:
Einicial = Efinal
Antes del choque, el sistema consiste en la energía Efoton de 1 MeV que lleva el fotón consigo mismo, más la energía en reposo del electrón mec² más la energía en reposo mnc² del núcleo pesado, y después del choque el sistema constará de la energía total del electrón en movimiento sumada a la energía en reposo del núcleo pesado:
Efoton + mec² + mnc² = γmec² + mnc²
1 MeV + 0.511 MeV = γ (0.511 MeV)
γ = 2.957
u = 0.941c
1 MeV + 0.511 MeV = γ (0.511 MeV)
γ = 2.957
u = 0.941c
Hay otros procesos de índole atómica en los cuales por la desintegración de un átomo también se tienen dos o más partículas resultantes cuyas masas sumadas no son iguales a la masa del átomo original (lo que llamamos un defecto de masa) pero en los cuales además de la energía cinética que se lleve consigo cada partícula resultante hay una energía pura liberada como energía radiante.
Existe una expresión muy útil que nos relaciona a la energía total E de un cuerpo con su momentum relativista p. Si la energía total del cuerpo es E = γm0c² = γE0 y su momentum relativista es p = γm0u, entonces usando E² = γ²E0² tenemos:
p² = γ²m0²u² = (γ² m0² c4) (u²/c4)
p² = γ² (m0c²)² (u²/c4) = γ² E0² u²/c4
Con esto:
E² - p² c² = γ² E0² (1 - u²/c²)
E² = p²c² + E0²
E² = p²c² + E0²
La relación anterior se puede memorizar mejor con la ayuda del siguiente “triángulo relativístico”:
El “triángulo relativístico” se traza empezando con el pie del triángulo que es la masa en reposo m0c² y levantando el otro cateto que representa la cantidad pc. Con un compás imaginario se tiende un arco hasta cortar a la hipotenusa. El segmento adicional a la longitud m0c² (que es la energía en reposo de la partícula) es el segmento K (que es la energía cinética de la partícula), segmentos que sumados dan la longitud total de la hipotenusa que es también la longitud total de la partícula. Aplicando entonces el teorema de Pitágoras a este triángulo rectángulo, obtenemos la siguiente relación:
(K + m0c²)² = (pc)² + (m0c²)²
PROBLEMA: ¿Cuál es la relación entre la energía y el momentum de un fotón de luz?
En virtud de que los fotones viajan a la velocidad de la luz, su masa en reposo, de acuerdo con la Teoría de la Relatividad, debe ser cero, y por lo tanto su energía debe ser totalmente cinética, energía radiante pura. Si un fotón existe, entonces debe estarse moviendo a la velocidad de la luz, y deja de existir en el momento en el que deja de moverse a esta velocidad (como cuando es absorbido por uno de los orbitales de un átomo de hidrógeno haciendo saltar a un electrón en dicho orbital a un nivel más alto de energía). Para una masa en reposo m0 igual a cero (y por lo tanto una energía en reposo E0 igual a cero), la relación relativista entre momentum y energía nos conduce a:
E² = p²c² + E0²
E = pc
E = pc
Se destaca aquí que esta relación es válida únicamente para un fotón, no para una partícula material.
PROBLEMA: Calcular la cantidad de movimiento de un electrón cuya velocidad es 0.8c, expresada en unidades MeV/c.
La cantidad de movimiento relativista está dada por p = γm0u. Entonces, con unas manipulaciones simples y usando el resultado anterior de m0c² = 0.511 Mev para el electrón:
p = γm0u = γm0c² (u/c²)
p = (1 /√1 - u²/c²) m0c² (u/c²)
p = (1 /√1 - (0.8)²) (0.511 MeV) (0.8/c)
p = 0.681 MeV/c
p = (1 /√1 - u²/c²) m0c² (u/c²)
p = (1 /√1 - (0.8)²) (0.511 MeV) (0.8/c)
p = 0.681 MeV/c
PROBLEMA: Calcular el momentum para un electrón de 1 MeV dando la respuesta en unidades MeV/c.
E² = p²c² + E0² = (pc)² + E0²
Se debe entender que la energía de 1 MeV es una energía cinética K. Entonces al electrón con energía cinética K = 1 MeV hay que sumarle su energía en reposo para obtener su energía total E ya que E = K + E0. Entonces:
(1 MeV + 0.511 MeV)² = (pc)² + (0.511 Mev)²
p = 1.42 MeV/c
p = 1.42 MeV/c
PROBLEMA: Calcular la energía cinética de un electrón cuyo momentum es de 3 MeV/c.
E² = p²c² + E0²
(K + E0)² = (pc)² + E0²
(K + E0)² = (pc)² + E0²
(K + 0.511 MeV)² = [(3 Mev/c) c]² + (0.511 MeV)²
K = √9.261 MeV² - 0.511 MeV = 2.53 MeV
K = √9.261 MeV² - 0.511 MeV = 2.53 MeV
PROBLEMA: Demostrar que la velocidad relativista de una partícula está dada por u = pc²/E.
Por un lado tenemos la expresión para el momentum relativista p = γm0u en donde el momentum p es una cantidad vectorial que tiene la misma dirección y sentido que la velocidad u de la partícula; y por el otro tenemos que la energía total E de la partícula es igual a γm0c². Entonces γm0 = E/c² y:
p = (E/c²) u
u = pc²/E
u = pc²/E
PROBLEMA: Demostrar que la rapidez de una partícula está dada por u = dE/dp.
Por un lado, de la definición de la magnitud del momentum relativístico, tenemos:
p = γm0u
Tomando diferenciales sobre lo anterior:
dp = d(γm0u) = m0d(γu) = m0 (γdu + udγ)
La expresión simplificada para ya la obtuvimos anteriormente, y es:
d(γm0u) = m0 {1 - u²/c²}-3/2 du
Por otro lado tenemos:
E = γm0c²
Tomando diferenciales:
dE = d(γm0c²) = m0c² dγ
La expresión para dγ también la obtuvimos ya con anterioridad, y es:
Entonces:
dE = m0c² (u/c²) {1 - u²/c²}-3/2 du
dE = (m0u) {1 - u²/c²}-3/2 du
La expresión para dγ también la obtuvimos ya con anterioridad, y es:
dγ = (u/c²) {1 - u²/c²}-3/2 du
Entonces:
dE = (m0u) {1 - u²/c²}-3/2 du
Dividiendo dE entre dp obtenemos:
dE/dp = {(m0u) {1 - u²/c²}-3/2 du} / { m0 {1 - u²/c²}-3/2 du}
dE/dp = u
dE/dp = u
En este problema hablamos de la rapidez de una partícula, en contraste con el problema anterior en el cual se habló acerca de la velocidad de la partícula, enfatizando el hecho de que la rapidez es una cantidad a la cual no se le asigna dirección y sentido en oposición a la velocidad que se representa vectorialmente por tener dirección y sentido. Así decimos que un carro tiene una rapidez u de 30 kilómetros por hora sin especificar dirección, pero el mismo carro tiene una velocidad u de 30 kilómetros por hora en el sentido Norte a Sur. La misma diferencia sutil manejada en la física clásica se sigue manejando en la Teoría de la Relatividad.