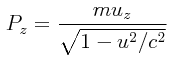Si bien hemos definido el momentum relativista y la energía relativista, es lógico suponer que ambas cantidades tomadas independientemente la una de la otra no permanecerán invariantes al pasar de un marco de referencia a otro. Podemos esperar que el simple momentum relativista P = γm0u cambie al pasar de un marco de referencia a otro en virtud de que con el cambio del marco de referencia la velocidad u de un cuerpo ya no será la misma para distintos observadores. Y de la energía relativista podemos afirmar otro tanto similar. Requerimos, pues, establecer las ecuaciones de transformación con las cuales dados el momentum relativista y la energía relativista de un cuerpo en cierto marco de referencia podamos obtener el momentum relativista y la energía relativista del mismo cuerpo en otro marco de referencia.
PROBLEMA: Obtener las transformaciones del momentum y la energía que deben ser utilizadas al pasar de un marco de referencia a otro cuando ambos marcos están moviéndose el uno con respecto al otro a una velocidad relativa V con respecto a sus ejes comunes alineados en x. Obtener asimismo las transformaciones inversas.
En el caso de la energía, puesto que la energía es una cantidad escalar que no posee dirección y sentido, sólo requerimos de una ecuación de transformación. En cambio el momentum, por ser una cantidad vectorial que definitivamente posee dirección y sentido, este momentum p tendrá tres componentes distintas en un sistema de coordenadas rectangulares (Cartesiano) que serán el triplete (px, py, pz).
Ya habíamos visto que el momentum relativista (dentro del marco de referencia S de un observador en reposo) de un cuerpo con masa propia m0 moviéndose a una velocidad u está dado por la relación:
p = γm0u² = m0u²/√1 - u²/c²
Por otro lado, ya habíamos visto también que la energía total del mismo cuerpo moviéndose a esa velocidad u está dada por la relación:
E = γm0c² = m0c²/√1 - u²/c²
Vamos a poner ahora a dicho cuerpo en un marco de referencia que está moviéndose a una velocidad V a lo largo del eje-x, dentro del cual el cuerpo tendrá una velocidad u’. Es importante recordar que esta velocidad u’ es una velocidad que no está confinada única y exclusivamente al eje-x, ya que puede tener componentes en los otros dos ejes que sumados vectorialmente nos dan la velocidad resultante u en el marco de referencia S’:
(u’)² = (u’x)² + (u’y)²+ (u’z)²
Obviamente, y del mismo modo, en el marco de referencia S:
(u)² = (ux)² + (uy)²+ (uz)²
Adoptaremos ahora una convención a la que nos aferraremos rígidamente. El símbolo γ lo reservaremos única y exclusivamente para denotar el movimiento relativo entre ambos marcos de referencia a lo largo de sus ejes comunes en la abcisa x a una velocidad V, o sea:
γ = /√1 - V²/c²
Lo anterior significa que, en ningún momento, intentaremos utilizar el símbolo γ para representar ya sea:
1/√1 - u²/c²
ó:
1/√1 - (u’)²/c²
Estas últimas dos expresiones las dejaremos tal cual. Esta aclaración es importante porque el tratar de asignarles el símbolo γ a cualquiera de ellas (ó ambas) puede ser causa de confusión posterior dificultando las derivaciones que estamos tratando de llevar a cabo.
Las componentes en un sistema de coordenadas rectangulares de la velocidad u del cuerpo en el marco de referencia S están relacionadas con las componentes en un sistema de coordenadas rectangulares de la velocidad u’ del cuerpo en el marco de referencia S’ de acuerdo con la suma relativista de velocidades que ya habíamos estudiado con anterioridad:
Dada la similitud de los cálculos algebraicos requeridos para obtener las transformaciones de momentum y energía de un marco de referencia a otro, llevaremos a cabo aquí una manipulación general que servirá para ambos casos. Podemos ver de ambas relaciones para el momentum y la energía que requerimos poner el denominador de ambas:
1/√1 - u²/c²
en función de u’x, u’y y de u’z, haciéndolo a través de u. Empezaremos primero por la relación:
u² = (ux)² + (uy)²+ (uz)²
introduciendo en la misma las tres transformaciones dadas arriba para la suma relativista de velocidades en cada uno de los tres ejes:
Elevando al cuadrado el lado derecho y poniendo todo bajo común denominador:
Entonces:
En el lado derecho de la igualdad, después de haber puesto todo bajo un común denominador, tenemos el siguiente numerador:
γ²c² (1 + Vu’x/c²)² - γ² (u’x + V)² - u’y² - u’z²
Como paso intermedio de simplificación, factorizaremos ahora a γ sacándolo del camino:
γ²[c² (1 + Vu’x/c²)² - (u’x + V)² - u’y²/γ² - u’z²/γ²]
Dentro de los paréntesis cuadrados, en relación a los dos últimos términos, tenemos 1/γ², que es igual a:
con lo cual:
Expandiendo los binomios cuadráticos y removiendo paréntesis:
Dentro de los paréntesis cuadrados, en relación a los dos últimos términos, tenemos 1/γ², que es igual a:
1/γ² = 1 - V²/c²
con lo cual:
γ²[c² (1 + Vu’x/c²)² - (u’x + V)² - u’y²(1 - V²/c²) - u’z²(1 - V²/c²)]
γ²[c² + 2Vu’x + V²u’x²/c² - u’x² - 2u’xV - V² - u’y² + V²u’y²/c² - u’z² + V²u’z²/c² ]
γ²[c² - V² + V²u’x²/c² - u’x² - u’y² + V²u’y²/c² - u’z² + V²u’z²/c²]
γ²[c² - V² + (u’x² + u’y²+ u’z²)V²/c² - (u’x² + u’y²+ u’z²)]
Para continuar simplificando el numerador, recurrimos a la relación dada arriba:
(u’x)² + (u’y)²+ (u’z)² = (u’)²
con lo cual podemos continuar adelante con la simplificación:
γ²[c² - V² + u’²V²/c² -u’²)]
γ²[c² - V² - u’²(1 - V²/c²)]
γ²[c²(1 - V²/c²) - u’²(1 - V²/c²)]
γ²[(1 - V²/c²)(c² - u’²)]
γ²c²(1 - V²/c²)(1 - u’²/c²)
Poniendo este numerador simplificado sobre el denominador:
γ²c² (1 + Vu’x ²/c²)²
entonces tras cancelarse mutuamente los factores γ²c² que hay arriba en el numerador y abajo en el denominador tenemos lo siguiente:
Invirtiendo ambos miembros de la igualdad y extrayendo raíz cuadrada:
Reestableciendo la cantidad γ subiendo √1 - V²/c² al numerador para formar 1/√1 - V²/c² :
Con esto, encontramos que la componente del momentum sobre el eje-x, Px, que está definida por la siguiente relación:
toma la siguiente forma con el resultado que obtuvimos arriba para 1/√1 - u²/c²:
Teniendo en mente que el desplazamiento relativo entre los marcos de referencia S y S’ ocurre únicamente a lo largo del eje-x, la componente del momentum sobre el eje-y, Py, está dada por:
Finalmente, la componente del momentum sobre el eje-z, Pz, está dada por:
En lo que respecta a la energía relativista, tenemos lo siguiente:
Utilizando las expresiones para el momentum y la energía en el marco de referencia S’, las expresiones anteriores pueden ser escritas de la siguiente manera:
Para obtener las transformaciones inversas simplemente despejamos de las transformaciones de energía y momentum obteniendo de este modo lo siguiente:
Las leyes de transformación para la energía y el momentum de un marco de referencia a otro no son difíciles de recordar en virtud de que son similares a las ecuaciones de transformación de Lorentz para la longitud y el tiempo. Comparemos las leyes de transformación para la energía y el momentum de un marco de referencia S a otro marco de referencia S’:
E = γ(E’ + Vp’x)
py = p’y
pz = p’z
px = γ(p’x + VE’/c²)
py = p’y
pz = p’z
px = γ(p’x + VE’/c²)
con las ecuaciones de transformación de Lorentz:
x = γ(x’ + Vt’)
y = y’
z = z’
t = γ(t’ + Vx’/c²)
y = y’
z = z’
t = γ(t’ + Vx’/c²)
Aunque se trata de cantidades físicas distintas, obsérvese la similitud entre ambos conjuntos de transformaciones. px se transforma como la coordenada espacial x, y la energía E se transforma como c²t. Esto nos hace sospechar que hay algo común de fondo en la similitud que hemos obtenido en las transformaciones.
Puesto que el tiempo y el espacio, ambos conceptos independientes en la física clásica, han sido unificados bajo un solo concepto en la interpretación geométrica de Minkowski de la Teoría Especial de la Relatividad, el concepto del espacio-tiempo, y han sido agrupados como componentes iguales bajo un solo vector cuatri-dimensional:
[ct, x, y, z]
entonces, ¿por qué no hacer lo mismo con el momentum y la energía relativistas, agrupándolos en igualdad de condiciones como los cuatro componentes de un vector cuatri-dimensional? Esto es precisamente lo que se ha hecho, adoptándose el uso del 4-vector energía-momentum conocido también como el 4-momentum:
P = [E/c, px, py, pz]
simbolizado con una letra P mayúscula, el cual también puede ser escrito como:
[E, pxc, pyc, pzc]
En ambos casos, las cuatro componentes del 4-vector energía-momentum ó 4-momentum deben tener la misma dimensión, ya sea de momentum o de energía.
Si escribimos las leyes de transformación del 4-vector energía-momentum utilizando notación de vectores columna:
entonces resulta obvio que podemos reescribir el lado derecho de esta ecuación vectorial como un producto de matrices:
que representa el siguiente sistema de ecuaciones:
E’ = γE - βγpxc + 0pyc + 0pzc
px’c = - βγE + γpxc + 0pyc + 0pzc
py’c = 0E + 0pxc + 1pyc + 0pzc
pz’c = 0E + 0pxc + 0pyc + 1pzc
px’c = - βγE + γpxc + 0pyc + 0pzc
py’c = 0E + 0pxc + 1pyc + 0pzc
pz’c = 0E + 0pxc + 0pyc + 1pzc
Esto amerita ser contrastado con la representación matricial de la transformación del 4-vector espacio-tiempo en un sistema de referencia S a un sistema de referencia S’:
Tanto en el caso en el que se involucra a 4-vectores energía-momentum como el caso en el que se involucra a 4-vectores espacio-tiempo bajo un esquema Lorentziano, la matriz de transformación resulta ser exactamente la misma.
De este modo, las definiciones como se han estado dando y las matemáticas del asunto nos indican que, de modo natural, todo lo que tiene que ver con la Teoría Especial de la Relatividad puede y debe ser manejado bajo un espacio cuatri-dimensional.
El haber juntado a la energía y el momentum como las cuatro componentes de un 4-vector está justificado también por la nueva invariante que nos produce. Ya habíamos anteriormente la siguiente expresión que nos relaciona la energía total de energía E de un cuerpo con la magnitud de su cantidad de movimiento p y su energía en reposo m0c²:
E² = (pc)² + (m0c²)²
Despejaremos a continuación el lado derecho de la ecuación dejando únicamente a la masa en reposo de dicho lado:
E² - (pc)² = (m0c²)²
El siguiente paso será dividir ambos miembros de la igualdad entre c² obteniendo:
(E/c)² - p² = m0²c²
Del lado derecho tenemos el producto de dos cantidades invariantes, porque la masa propia m0 de un cuerpo debe ser la misma en cualquier sistema de referencia, y la velocidad de la luz c también es una invariante absoluta de acuerdo con el segundo postulado de la Teoría Especial de la Relatividad. Entonces el lado derecho de la ecuación es una invariante, y en virtud de la igualdad el lado izquierdo de la ecuación también debe ser una cantidad invariante. Esto significa que para dos sistemas de referencia distintos S y S’ en los cuales para el mismo cuerpo:
E² = (pc)² + (m0c²)²
E’² = (p’c)² + (m0c²)²
debemos tener:
E² - (pc)² = E’² - (p’c)²
o bien:
(E/c)² - p² = (E’/c)² - p’²
Al haber obtenido una nueva invariante, además de otras que iremos obteniendo al adentrarnos en el tema de la Teoría General de la Relatividad, debe irse despejando la creencia de que en la Teoría de la Relatividad todo es relativo. Aunque el movimiento dejó de ser absoluto, Einstein introdujo un nuevo absoluto en su segundo postulado, la velocidad de la luz, tras lo cual fueron apareciendo nuevos absolutos como las invariantes que hemos estado descubriendo. Es falso, pues, que en la Teoría de la Relatividad todo es relativo.
La representación combinada de la energía y el momentum relativistas en un 4-vector nos resume dos principios fundamentales de la dinámica, la conservación del momentum y la conservación de la energía, en un solo paquete. Igualando los componentes de un 4-vector antes y después de un choque o de una interacción podemos resolver los problemas que requieren de dichos principios para su resolución. Un ejemplo de tales problemas es el de un fotón de energía E0 que choca contra un electrón inicialmente en reposo, saliendo en retroceso el electrón a un ángulo φ y a una velocidad V, mientras que el fotón es dispersado con una energía (menor) E a un ángulo θ: