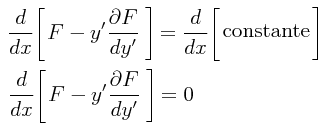PROBLEMA: Demostrar que la menor distancia entre dos puntos en un espacio tri-dimensional Euclideano es una línea recta.
En un espacio tri-dimensional Euclideano, el elemento de la distancia es:
ds² = (dx)² + (dy)² + (dz)²
O bien:
ds = √(dx)² + (dy)² + (dz)²
Para poder describir una una línea cualesquiera en el espacio tri-dimensional Euclideano necesitamos recurrir a ecuaciones paramétricas en las que en este caso cada una de las variables que representan los tres ejes coordenados dependerá de un parámetro independiente que llamaremos t, el cual podemos identificar como el tiempo para facilitar nuestra comprensión del problema. En otras palabras, cada una de las variables x, y y z serán funciones del parámetro t. Siendo así, entonces podemos llevar a cabo la integración de un punto t1 a otro punto t2:
Para poder utilizar la ecuación de Euler con la finalidad de determinar la ruta extrema entre t1 y t2, identificamos en este caso a la función F de dicha ecuación como la siguiente:
Obsérvese que estamos llevando a cabo una simplificación representando cada una de las derivadas con respecto a t mediante un punto colocado encima de cada variable y prescindiendo de la forma explícita de representar dichas derivadas.
En este caso, tendremos tres ecuaciones de Euler, las cuales son:
Obviamente, la función F ya no depende directamente ni de x ni de y ni de z, porque estas variables no aparecen como tales en la expresión para F (notacionalmente, una variable cualquiera es diferente de la misma variable que tenga un punto colocado encima, y no deben ser confundidas en el proceso de manipulación matemática). Con esto, tenemos que:
Entonces las tres ecuaciones de Euler originales se nos reducen a:
Substituyendo la relación para F en estas expresiones y llevando a cabo la integración con respecto al tiempo obtenemos:
Combinando las tres ecuaciones obtenidas, tenemos entonces:
Llevaremos ahora a cabo una integración sobre estas expresiones de un tiempo t1 a un tiempo arbitrario t, obteniendo lo siguiente:
Ahora repetiremos el procedimiento integrando las mismas expresiones pero de un tiempo t1 a un tiempo t2 obteniendo así:
Esto nos permite hacer las substituciones apropiadas para poder obtener los valores de las constantes de integración C1, C2 y C3 llegando a lo siguiente:
Esta es precisamente la ecuación de una recta en el espacio tri-dimensional Euclideano que pasa por los puntos P(x1, y1, z1) y Q(x2, y2, z2).
En algunos problemas es ventajoso recurrir a ciertos “trucos” que a veces se descubren accidentalmente y en otras ocasiones son el fruto de la experiencia y la madurez del que está trabajando sobre problemas de esta índole. Uno de dichos trucos será detallado a continuación.
PROBLEMA: Demuéstrese que si la función F en la integral:
es independiente de la variable x, entonces la integral es un extremo si:
Fy - y’Fy’ = constante
o bien, en forma explícita:
El diferencial total de F, cuando es una función de dos variables y y y’ es:
Obsérvese que el término (∂F/∂x) dx no fue incluído en la suma de términos puesto que la función F es independiente de x.
Dividiendo ambos lados entre el diferencial dx y simplificando mediante la toma de las derivadas:
Tomaremos ahora la expresión:
Fy - y’Fy’
y obtendremos la derivada de la misma con respecto a x, que viene siendo:
Tomaremos ahora la derivada con respecto a x del segundo término, y reemplazaremos en el primer término del lado derecho de esta ecuación la expansión obtenida arriba para dF/dx, cancelando los dos términos comunes que se anulan mutuamente (puestos en color rojo):
lo cual se nos simplifica a:
Factorizando y' tenemos que esto es igual a:
Entonces tenemos que:
Por otro lado, si:
Fy - y’Fy’
es igual a una constante, entonces la derivada de esto debe ser igual a cero:
Entonces lo que tenemos se nos reduce a:
Puesto que y’ = dy/dx se asume diferente de cero, esto sólo puede ser cierto si:
que es la ecuación de Euler, la condición esencial para que haya un extremo. Por lo tanto, si:
y si F es independiente de x, entonces la integral:
será un extremo.
PROBLEMA: Encontrar la geodésica que hay entre dos puntos situados sobre la superficie de una esfera.
Como siempre, el elemento de distancia en un espacio tri-dimensional está dado por:
ds² = (dx)² + (dy)² + (dz)²
o bien:
ds = √(dx)² + (dy)² + (dz)²
Para poder expresar el elemento de distancia en coordenadas esféricas recurrimos a las relaciones que conectan las coordenadas Cartesianas (x,y,z) con las coordenadas esféricas (r,θ,φ):
x = r sen θ cos φ
y = r sen θ sen φ
z = r cos θ
y = r sen θ sen φ
z = r cos θ
No es difícil demostrar mediante estas relaciones que el elemento de línea ds² está dado por:
ds² = dr² + r² dθ² + r² sen²θ dφ²
Puesto que estamos interesados en obtener la geodésica sobre la superficie de una esfera, en este problema el radio r se mantendrá constante en todo momento sin ser objeto de variación alguna. Esto significa que dr = 0. Entonces el elemento de línea sobre la superficie de la esfera está dado por:
ds² = r² dθ² + r² sen²θ dφ²
ds = r √dθ² + sen²θ dφ²
Entonces, sacando fuera del radical a dφ, la distancia entre dos puntos cualesquiera 1 y 2 sobre la superficie de la esfera será igual a:
Si lo que estamos buscando es la geodésica, la ruta extrema entre los puntos 1 y 2 (la cual puede ser un mínimo o un máximo) entonces bajo el criterio de la ecuación de Euler identificamos como F a:
Para poder continuar, utilizaremos la siguiente representación notacional:
con lo cual podemos escribir lo siguiente:
Utilizaremos ahora la “segunda forma” de la ecuación de Euler:
con la cual podemos escribir lo siguiente:
Diferenciando y multiplicando al través por F, tenemos entonces:
Esto puede ser resuelto para dφ/dθ (obsérvese que no estamos resolviendo para dθ/dφ, en virtud de que este ligero cambio nos resulta en una simplificación posterior para obtener la respuesta que buscamos), produciéndonos:
Despejando para φ y llevando a cabo la integración obtenemos la siguiente relación:
en donde κ es la constante de integración y α es utilizada para representar:
α² = (1 - C²)/C²
Reescribiendo lo anterior para ponerlo en función de θ, o mejor dicho cot(θ):
cot(θ) = α sen(φ - κ)
Este es un resultado en coordenadas esféricas que no nos ilustra mucho sobre la naturaleza de la geodésica. Para poder obtener mayor claridad, es necesario revertir a coordenadas rectangulares (Cartesianas) multiplicando ambos miembros por r senθ para obtener después de haber llevado a cabo la expansión de sen(φ - κ):
(α cos κ) r senθ senφ - (α sen κ) r senθ cosφ = r cosθ
Por razones que serán obvias pronto, no eliminaremos la variable r como podríamos hacerlo al aparecer como factor en ambos lados de la ecuación.
Siendo κ y α constantes, podemos compactarlas bajo los nombres de otras constantes que las agrupen:
A = α cos κ
B = α sen κ
B = α sen κ
Esto nos produce:
A (r senθ senφ) - B (r senθ cosφ) = r cosθ
Pero de las transformaciones de coordenadas esféricas a coordenadas Cartesianas se sabe que:
x = r senθ cosφ
y = r senθ senφ
z = r cosθ
y = r senθ senφ
z = r cosθ
Entonces lo que tenemos es esencialmente:
Ay - Bx = z
En el espacio tri-dimensional Euclideano, esta es precisamente la ecuación de un plano que corta a la esfera pasando por el centro de la misma. Se concluye que la geodésica es la curva que dicho plano forma con la intersección de la superficie de la esfera, en pocas palabras, un círculo máximo, definido como aquél que corta a una esfera en dos partes iguales:
Obsérvese que en el caso de la geodésica de la esfera, el círculo máximo incluye tanto la distancia máxima como la distancia mínima entre dos puntos cualesquiera de la superficie de la esfera, dependiendo del que entre dos puntos cualesquiera sobre la superficie de la esfera nos movamos siguiendo el camino en el cual recorremos el ángulo esférico más corto que hay entre dichos puntos (llamémoslo ω), o el ángulo máximo que hay entre dichos puntos (2π - ω), como nos lo muestra la siguiente figura en la cual tenemos a la izquierda (en color rojo) la ruta más corta posible a lo largo de la geodésica y tenemos a la derecha (también en color rojo) la ruta más grande posible a lo largo de la geodésica:
La distancia mínima será indudablemente aquella en la cual gastaremos la menor cantidad de gasolina si nos movemos en un vehículo motorizado para llegar de un punto a otro. ¿Pero y la distancia máxima? Aquí la cosa parecería menos clara, porque ciertamente hay muchas otras rutas que podemos tomar siguiendo la ruta contraria tomando muchas desviaciones en el camino. Sin embargo, sólo una de ellas será la ruta “más derecha” posible.
Este problema nos ilustra otra situación en la que los estudiantes expuestos por vez primera a la obtención de máximos y mínimos mediante las herramientas del cálculo infinitesimal no tienen problema alguno. En el cálculo infinitesimal, si queremos obtener el máximo o el mínimo de alguna función, tomamos simplemente la derivada de la función e igualamos a cero, y tras esto tomamos la segunda derivada para determinar mediante el cambio de signo si lo que tenemos es un máximo o un mínimo (o varios máximos y varios mínimos). En el caso de la ecuación de Euler, no existe un procedimiento general para saber de antemano si lo que hemos obtenido es un máximo o un mínimo, todo lo que sabemos es que hemos obtenido un extremo. Afortunadamente, en el caso que nos ocupa, la naturaleza del extremo será obvia por las circunstancias de cada problema que se vaya considerando.
Habiendo dejado en claro la forma en la cual trabaja la ecuación de Euler para obtener el extremo de una función F que aparece bajo el signo de una integral, y habiendo dejado en claro también la forma en la cual se obtiene dicha ecuación, estamos preparados para dar el salto del espacio tri-dimensional Euclideano al espacio 4-dimensional relativista, para lo cual la ecuación geodésica deberá formularse bajo el esquema más amplio posible, el esquema del cálculo tensorial. Pero antes de ello, haremos un repaso de la derivación de la ecuación de Euler con la pequeña diferencia de que en esta ocasión meteremos a la variable tiempo como tal.
PROBLEMA: Demostrar que una condición necesaria para que:
sea un extremo es que:
Obsérvese que estamos utilizando la notación del punto puesto encima de la variable x, lo cual en este caso indica que se trata de la derivada de x con respecto al tiempo, dx/dt, considerada en sí como una nueva variable.
Procedemos en esta derivación de la misma forma como lo hicimos para la ecuación de Euler en la que la variable tiempo no estaba involucrada explícitamente.
Sea x = X(t) la curva que hace a la integral I extrema entre los tiempos t1 y t2. Entonces cualquier otra curva estará dada por:
x = X(t) + αη(t)
en donde α es un factor de escala independiente del tiempo que nos dá la magnitud de la variación y η(t) es una función desconocida arbitraria excepto por el requerimiento de que todas las rutas alternas pasen también por los puntos t1 y t2 en donde la variación debe ser cero, o sea:
η(t1) = 0
η(t2) = 0
η(t2) = 0
Entonces, si la curva óptima que extremiza (minimiza) a la integral es x = X(t), cualquier otra ruta alterna estará dada por:
x = X(t) + αη(t)
Abreviaremos notacionalmente para simplicidad sin olvidar la dependencia sobre la variable x:
x = X + αη
Tomando diferenciales con respecto a la variable tiempo:
x’ = dx/dt = X’ + αη’
Al tomar la derivada con respecto al tiempo, en muchos textos y trabajos con la Relatividad General se acostumbra utilizar la notación de punto poniendo un punto encima de la variable en lugar de la comilla, y tal cosa haremos aquí también:
La integral I a ser extremizada es la siguiente:
y la condición para obtener un valor extremo en α = 0, análoga a la derivada dy/dx igualada a cero en el cálculo infinitesimal ordinario será:
[∂I(α) /∂α]α = 0 = 0
Extremizamos (minimizamos) ahora la integral tomando la derivada de la integral I con respecto al parámetro α manteniendo todo lo demás constante:
I'(α) = ∂I(α) /∂α
De nueva cuenta, esto requiere llevar a cabo una diferenciación metiendo al símbolo ∂ dentro del símbolo ∫, o sea efectuando una diferenciación bajo el símbolo de la integral, lo cual podemos hacer en virtud de que la diferenciación la estamos llevando a cabo con respecto a la variable α y no con respecto a la variable dt sobre la cual se efectúa la acción del integrando:
Al segundo término en esta integral se le puede aplicar una integración por partes:
Puesto que η(t1) = η(t2) = 0, la parte integrada es igual a cero, con lo cual:
Juntando esto nuevamente con el primer término de la integral original, tenemos entonces:
Para que esto sea cierto lo que tenemos dentro del paréntesis debe ser cero, ya que siendo η arbitrario si lo escogemos diferente de cero no hay otra forma de hacer la expresión de la izquierda igual a cero más que igualando todo lo que hay dentro de los paréntesis a cero. Se concluye de lo anterior que:
Este resultado se puede extender fácilmente a cualquier cantidad n de coordenadas repitiendo mecánicamente los pasos llevados a cabo arriba para una integral a ser extremizada que tenga la siguiente forma:
obteniendo no una sino varias ecuaciones de Euler, un total de n ecuaciones, una para cada coordenada:
El siguiente paso consistirá en extender el concepto de la geodésica de un espacio tri-dimensional Euclideano hacia la geodésica en un espacio 4-dimensional propio de la Teoría de la Relatividad, el espacio-tiempo curvo. Para ello, podemos extender sin dificultad alguna el concepto de la ecuación de Euler usado para encontrar la longitud más corta sobre una superficie en un espacio de tres dimensiones (como lo es el caso de una esfera) hacia el espacio de cuatro dimensiones, obteniendo así la ecuación de la geodésica entre dos puntos cualesquiera de dicho espacio 4-dimensional. No hay nuevos principios matemáticos involucrados ni nuevas ideas, se trata únicamente de extender el concepto de la geodésica hacia un plano multi-dimensional. Es precisamente así como se obtiene la ecuación general de la geodésica en un espacio-tiempo curvo propio de la Teoría General de la Relatividad.
No hay que perder de vista el hecho de que la geodésica, por ser a fin de cuentas una distancia, un número medido en metros, kilómetros o millas, sin dirección y sentido, es algo que esperamos que permanezca invariable bajo cualquier transformación de coordenadas.
PROBLEMA: Derivar las ecuaciones geodésicas para un espacio multi-dimensional que pueda ser Euclideano o no-Euclideano.
Empezaremos por la definición más general de todas que se le pueda dar a un elemento infinitesimal de distancia, en la cual interviene desde luego el tensor métrico g:
ds² = gpq xp xq
Cabe recordar, por la importancia de lo mismo, que aquí está siendo utilizada rígidamente la convención de sumación para índices repetidos. Esta definición general, dada por Bernhard Riemann, puede ser utilizada para definir una distancia Euclideana como la siguiente (teorema de Pitágoras extendido a cualquier número de dimensiones):
ds² = (x1)² + (x2)² + (x3)² + (x4) + (x5)²
o para definir un intervalo relativista en un espacio-tiempo plano:
ds² = (x1)² - (x2)² - (x3)² - (x4)
o cualquier otro tipo de distancia que queramos definir. Todo depende de la métrica.
Si en vez de utilizar simplemente ds utilizamos ds/dt, o sea la derivada con respecto al tiempo, entonces tenemos lo siguiente (la convención de sumación seguirá vigente en todo lo que resta de la solución del problema):
Tensorialmente hablando, lo que queremos encontrar es el extremo de:
Para ello, recurriremos a la ecuación de Euler, al igual que como lo hicimos en todos los problemas anteriores. Pero obviamente, esto requerirá no una sino varias ecuaciones de Euler para el caso más general que involucra varias variables, como lo es el caso de la Relatividad General.
Haciendo la identificación:
la especificación de cada una de las ecuaciones de Euler requeridas es inmediata. Cada una de las ecuaciones de Euler para cada una de las coordenadas xk estará dada por:
En el caso de la Relatividad General, puesto que tenemos un espacio 4-dimensional especificado mediante cuatro coordenadas generalizadas, tendremos un sistema de cuatro ecuaciones. El procedimiento que llevaremos a cabo será válido para cualquier espacio n-dimensional.
Obtendremos primero ∂F/∂xk:
Ahora procedemos a obtener la otra derivada:
Obsérvese que en esto se ha tenido que llevar a cabo un cambio en el sub-índice q de gpq haciéndolo gpk como lo muestra el siguiente paso intermedio que se empleó arriba:
en virtud de que dentro de la doble sumatoria (implícita en los sub-índices de acuerdo a la convención de sumación):
mientras que:
e igualmente:
viniendo el factor 2 del hecho de que el tensor métrico g es simétrico, o sea gij = gji.
De lo dicho arriba para ds/dt, usando:
tenemos entonces que las ecuaciones de Euler para cada una de las coordenadas xk estarán dadas por:
Tomando la derivada con respecto al tiempo e invirtiendo el orden de los términos (lo cual equivale simplemente a cambiar los signos):
Obsérvese que hemos utilizado aquí la notación del doble punto o punto repetido puesto encima de la variable para simbolizar la derivada de segundo orden de la coordenada xk. Aquí podemos introducir los símbolos de Christoffel. Escribiendo:
tenemos entonces la siguiente conclusión:
Si tomamos a la longitud s del arco como parámetro, de modo tal que:
el resultado obtenido se nos convierte en lo siguiente:
Si multiplicamos ahora todo por grk, en el primer término tendremos primero:
con lo cual el primer término quedará convertido en lo siguiente al llevarse a cabo la contracción sobre los índices repetidos p como lo marca la convención de sumación sobre la doble sumatoria:
mientras que en el segundo término el efecto de multiplicar grk por el símbolo de Christoffel de primer género será elevar el índice k de dicho símbolo convirtiéndolo en un símbolo de Christoffel de segundo género:
De este modo, obtenemos finalmente:
Estas son las ecuaciones geodésicas para un espacio multi-dimensional que puede ser Euclideano o no-Euclideano, el cual es mejor conocido como espacio de Riemann. Es un sistema de ecuaciones diferenciales de segundo orden que tiene que ser resuelto para poder determinar la trayectoria a lo largo de las geodésicas. Si llevamos a cabo un ligero cambio notacional haciendo r = β, p = σ y q = α, revirtiendo además hacia la notación de punto, podemos poner esto mismo en una forma que resultará familiar a quienes ya han hojeado o estudiado textos convencionales de Relatividad General:
Esta ecuación fácilmente memorizable es también conocida como la ecuación geodésica, junto con las ecuaciones de campo de la Relatividad General, nos dá una especificación matemática completa para el comportamiento de un sistema físico. De este modo, cualquier problema propio de la Relatividad General se convierte en un problema de índole meramente matemática. Pero es importante destacar que la ecuación es completamente general, y se puede utilizar para la búsqueda de geodésicas tanto dentro de la Relatividad General como en la resolución de problemas clásicos como los que ya hemos visto.
En una geometría Euclideana de cuatro dimensiones, en donde todas las dimensiones son dimensiones espaciales, la geodésica es “la línea más derecha posible de todas”. Esto es válido para toda geometría Euclideana en donde se cumple el quinto postulado de Euclides que nos dice: “a través de un punto externo a una recta dada sólo es posible trazar una recta paralela a la recta dada”. Pero obviamente el quinto postulado no se cumple en una geometría no-Euclideana como la que tiene lugar sobre la superficie de una esfera. En cualquier parte de la esfera, si trazamos dos rectas perfectamente paralelas (por ejemplo, formando ambas un ángulo de 90 grados con el Ecuador) y las extendemos indefinidamente sobre la superficie de la esfera, las rectas eventualmente se encontrarán:
De cualquier manera, aún en una geometría no-Euclideana, la geodésica sigue siendo “la línea más derecha posible de todas” entre dos puntos, sigue siendo la ruta que representa la menor distancia posible entre dichos puntos, la que nos llevaría el menor tiempo posible recorrer. En la geometría Euclideana, dos geodésicas inicialmente paralelas permanecen paralelas, nunca se cruzan ni divergen la una de la otra (como ocurre sobre la superficie de un hiperboloide con forma de silla de montar). Nosotros describimos esta situación diciendo que este tipo de geometría es una geometría plana. Por otro lado, sobre la superficie de una esfera dos geodésicas inicialmente paralelas convergen la una hacia la otra y eventualmente se cruzan. Nosotros describimos esta situación diciendo que este tipo de geometría es una geometría curva.
El lector debe prepararse ahora para una sorpresa.
Si bien en cualquier geometría Euclideana o inclusive en cualquier geometría no-Euclideana bajo cualquier número de dimensiones espaciales que se nos antoje postular la geodésica es la ruta que representa la menor distancia posible entre dos puntos cualesquiera, en la geometría no-Euclideana del espacio-tiempo relativista en donde tenemos tres dimensiones espaciales y una dimensión de tiempo la estructura de la geodésica es tal que aunque sigue siendo “la ruta más derecha posible de todas” la geodésica no es la trayectoria mínima sino la trayectoria máxima de todas las trayectorias posibles, en pocas palabras no es la menor distancia posible en el espacio-tiempo sino la mayor distancia posible. Esto tiene una consecuencia muy curiosa con la que todos estamos familiarizados. Un cuerpo que se mueva bajo la influencia de la gravedad se moverá recorriendo la ruta que le lleva el mayor tiempo posible recorrer de acuerdo con su reloj propio. En su libro ABC of Relativity: Understanding Einstein publicado en 1925, Bertrand Russell llama a esto la “ley de la pereza cósmica” - los cuerpos dejados a sí mismos se toman el mayor tiempo posible para llegar a su destino. Un cuerpo cualquiera, dejado a sí mismo, viaja de modo tal que el tiempo que le lleva efectuar el recorrido, de acuerdo con su propio reloj, es el mayor tiempo posible. Si hubiera viajado tomando cualquier otra ruta de un evento a otro, el tiempo sería menor.
¿Pero cómo es esto posible?, se preguntará el lector. En primer lugar, en los problemas matemáticos del cálculo de variaciones, una de las primeras cosas que confronta el matemático es el hecho de que la solución que obtiene a un problema es una solución extrema, la cual no necesariamente es un mínimo sino que puede ser también un máximo. La razón por la cual la solución matemática al problema del recorrido entre dos puntos resulta ser la que toma el mayor tiempo posible es porque el tipo de intervalo que estamos considerando no es un mero intervalo espacial sino un intervalo relativista que es más análogo a la dimensión del tiempo que a la dimensión de longitud. De este modo, la Luna en su movimiento de rotación alrededor de la Tierra escoge su ruta de modo tal que cualquier pedacito de dicha ruta representa una mayor “distancia” que cualquier otra ruta alterna. Pero esta es una distancia espacio-tiempo. Si nosotros pensamos que la geodésica está dada por la menor distancia posible entre dos puntos, entonces estamos pensando en una geodésica puramente espacial. Pero si pensamos que la geodésica está dada por la mayor distancia posible entre dos puntos, entonces estamos pensando en una geodésica espacio-tiempo, una geodésica relativista. Las trayectorias elípticas de los planetas alrededor del Sol son precisamente geodésicas relativistas. Las trayectorias parabólicas de los cometas que suelen visitarnos de vez en cuando son también geodésicas relativistas.
Pero si un cuerpo cualquiera dejado a sí mismo viaja de modo tal que el tiempo que le lleva efectuar cualquier recorrido, de acuerdo con su propio reloj, es el mayor tiempo posible, ¿no podría entonces tomarse un tiempo infinitamente grande para llegar de un punto a otro? Definitivamente, no, porque el recorrido tiene que hacerlo a lo largo de la geodésica 4-dimensional, o sea la ruta más corta posible en el espacio-tiempo relativista. Esto es similar a los arcos del circulo máximo que en el espacio Euclideano tri-dimensional representan la solución a la ecuación de Euler sobre la superficie de una esfera; entre dos puntos cualesquiera uno de los arcos cuyos extremos están situados en dichos puntos será un arco de menor longitud (mínimo) mientras que el otro será el de mayor longitud (máximo), las geodésicas fijan la ruta a seguir, y no hay infinitos involucrados.
Para poder estudiar en mayor detalle la forma en la cual hacemos un recorrido de un punto P a un punto Q en el espacio-tiempo relativista, debemos considerar cualquier recorrido que llevemos a cabo como un recorrido formado por una cantidad infinitamente grande de intervalos relativistas infinitamente pequeños:
ds² = (dct)² - (dx)² - (dy)² - (dz)²
Toda geodésica relativista se puede considerar formada por segmentos de intervalos relativistas infinitesimales. Aquí podemos definir tres tipos de geodésicas en el espacio-tiempo:
1) Geodésicas tipo temporal (timelike).- Aquellas en las que en un intervalo relativístico predomina el componente temporal sobre el componente espacial,
2) Geodésicas tipo espacial (spacelike).- Aquellas en las que en un intervalo relativístico predomina el componente espacial sobre el componente temporal
3) Geodésicas tipo luminoso (lightlike).- Aquellas en las que en un intervalo relativístico el componente espacial es igual al componente temporal.
En la Teoría Especial de la Relatividad, dos observadores inicialmente en reposo el uno frente al otro permanecen en reposo manteniendo una separación espacial constante, y entonces dos geodésicas tipo temporal inicialmente paralelas se mantendrán paralelas. El mismo argumento se puede extender hacia las geodésicas tipo espacial y tipo luminoso. Al no cruzarse jamás dichas geodésicas, se concluye que en la Teoría Especial de la Relatividad, la geometría del espacio-tiempo es Euclideana, es decir, plana, es una geometría en donde se cumple el quinto postulado de Euclides que nos afirma que dos rectas paralelas se mantienen paralelas sin cruzarse y sin divergir la una de la otra. Es el tipo de geometría descrita por las transformaciones de Lorentz. Y en contraste, en la Teoría General de la Relatividad, la geometría del espacio-tiempo es curva, es una geometría en donde no se cumple el quinto postulado de Euclides porque es una geometría en donde las rectas paralelas no pueden existir.