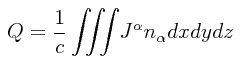Electrodinámica relativista III

Aunque este tema correponde más bien a la Teoría Especial de la Relatividad que a la Relatividad General, se ha puesto aquí siguiendo no sólo la metodología pedagógica que indica que los temas deben ser puestos en orden ascendente de dificultad sino tomando en cuenta el hecho de que el tratamiento del tema requiere de un conocimiento previo del análisis tensorial que no se acostumbra dar en un curso introductorio de la Teoría Especial de la Relatividad pero que es mandatorio antes de entrar de lleno en el tema de la Relatividad General. Este tema requiere de cierta familiaridad con las nociones básicas del electromagnetismo.

El tensor de Faraday F, tan importante para el tratamiento tensorial dado a la electrodinámica clásica, puede ser a su vez definido en términos de un potencial electromagnético A utilizándolo como punto de partida, a manera de axioma o postulado Euclideano, para el desarrollo de todo lo demás. La definición del tensor de Faraday en su forma covariante sobre esta base es la siguiente:

El potencial electromagnético A es, desde luego, un tensor, cumpliendo con la definición básica de un tensor:

PROBLEMA: Demostrar que, bajo una transformación de coordenadas al pasar de un sistema de referencia S a otro sistema de referencia S’, la definición del tensor de Faraday F en función del potencial electromagnético A cumple con la definición fundamental de un tensor.

En el sistema de referencia S’, la definición covariante del tensor de Faraday F, si es que ha permanecido realmente invariante en forma, debe tener el siguiente aspecto:

Puesto que A es un tensor, lo podemos substituír aquí por su definición tensorial básica:

Desarrollando y simplificando tenemos entonces:

Lo último es precisamente la definición de un tensor covariante de orden dos. Se concluye que el tensor de Faraday, definido en términos del potencial electromagnético A, es un tensor.

Siendo el tensor de Faraday F un tensor, en el pleno sentido de la palabra, podemos tomar la derivada covariante de dicho tensor, lo cual nos introduce los símbolos de Christoffel de la siguiente manera (como siempre, usamos el semicolon para denotar la derivación covariante y la coma para denotar la derivación ordinaria):

F_αβ;γ = F_αβ,γ - Γ^μ_αγF_μβ - Γ^μ_βγF_αμ

Se vuelve necesario advertir aquí que la reformulación tensorial de las leyes de la electrodinámica de Maxwell sólo es válida para las leyes de Maxwell en el vacío, o sea para campos electromagnéticos propiamente dichos, conocidas también como las leyes “microscópicas” de Maxwell. Para las leyes “macroscópicas” de Maxwell aplicadas a materiales de todo tipo, la presencia de dichos materiales establece un marco de referencia fijo con lo cual las leyes dejan de ser covariantes. Las ecuaciones de Maxwell para el campo electromagnético macroscópico en la materia pueden ser deducidas de las ecuaciones de Maxwell postuladas para el campo electromagnético microscópico. La influencia de la materia es lo que dá origen a una densidad de carga eléctrica microscópica y a una densidad de corriente eléctrica microscópica. Como tales, los electrones producen cambios espaciales rápidos en el campo electromagnético.

El tensor de Faraday es utilizado tanto en el estudio de los campos electromagnéticos como de las cargas eléctricas en movimiento. Para que las formulaciones tensoriales puedan ser covariantes, invariantes en forma al pasar de un sistema de referencia S a otro sistema de referencia S’, es necesario reformular las variaciones con respecto al tiempo en función del tiempo propio (local) τ medido por un observador situado en el sistema en reposo, y se vuelve necesario reformular también las definiciones dadas clásicamente en el 3-espacio Euclideano de modo tal que puedan ser enunciadas en función de 4-vectores. Un buen ejemplo de ello lo tenemos en la ecuación de Lorentz para una carga eléctrica en movimiento. Clásicamente, el campo eléctrico E está dado en función de la fuerza de atracción (o repulsión) F_E que actúa sobre una carga de prueba situada a cierta distancia de la carga puntual que está generando dicho campo, mientras que la fuerza F_B que actúa sobre una carga en movimiento cuando está viajando dentro de un campo de inducción magnética B está dada en función del producto cruz de la velocidad u de la carga y la intensidad B del campo magnético.

La fuerza total F que actúa sobre la carga será igual a la suma vectorial de F_E y de F_B:

Puesto que, clásicamente, la fuerza dinámica actuando sobre una partícula es por definición igual al cambio en su cantidad de movimiento, dp/dt, el lado izquierdo de la expresión anterior lo podemos escribir de la siguiente manera:

Esta es la ecuación de fuerza de Lorentz, una expresión clásica pre-relativista, válida en el 3-espacio Cartesiano únicamente para velocidades suficientemente bajas en comparación con la velocidad de la luz. Vamos a tratar ahora de reformular esta última ecuación para que sea covariante, invariante bajo transformaciones de Lorentz. Antes de continuar, es importante aclarar de antemano que un postulado esencial en la electrodinámica relativista es el de la invariancia de la carga eléctrica, o sea que la carga eléctrica de una partícula es una cantidad cuya magnitud no cambia, se conserva absolutamente sin variar al pasar la partícula de un sistema de referencia a otro. La invariancia de la carga bajo transformaciones de Lorentz, o más concretamente, la independencia de la velocidad de la carga observada de una partícula, es algo establecido experimentalmente que no resulta de teoría alguna.

En la ecuación de fuerza de Lorentz, el momentum p de la partícula consta de tres componentes:

p = (p_x, p_y, p_z)

Si este momentum p forma parte de un 4-vector, tal vector no puede ser otro más que el 4-vector energía-momentum P que ya hemos estudiado con anterioridad:

P = (p^α) = (p¹, p) = (E/c, p_x, p_y, p_z)

Pero el 4-momentum relativista P es simplemente el producto de la masa propia m_o por cada una de las componentes de la 4-velocidad U = (U^α) de la Teoría Especial de la Relatividad, o sea:

P = (m_oU¹, m_oU) = m_oU^α

Si usamos el tiempo propio (local) τ en lugar del tiempo absoluto t para la diferenciación, entonces la ecuación de fuerza de Lorentz puede ser escrita de la siguiente manera para el 4-espacio:

El lado izquierdo lo podemos poner también en función de la 4-velocidad U = (U^α):

Podemos introducir además el tensor de Faraday F para escribir de este modo ambos lados de la 4-fuerza de Lorentz en notación tensorial de componentes:

Ambos lados de esta expresión están escritos en función de la 4-velocidad U. Si queremos escribirlos en función de la 4-posición, entonces la expresión resultante es la siguiente:

PROBLEMA: De la definición básica del 4-vector densidad de corriente J:

J = (cρ, J)

podemos ver que la carga eléctrica total Q en cualquier marco de referencia es:

en donde la integración múltiple se extiende sobre una hipersuperficie t = constante. Si definimos a n como un vector unitario normal a esta hipersuperficie, demostrar que:

En un 3-espacio Euclideano, el 3-vector n = (n₁, n₂, n₃) es un vector unitario normal (perpendicular) a un elemento de una 2-superficie dS, de modo tal que el flujo de un vector A a través de dicha superficie es:

A · dS = A · n dS = (A¹, A², A³) · (n₁, n₂, n₃) dS

= (A¹n₁ + A²n₂ + A³n₃) dS = A^α n_α dS

En el 4-espacio relativista, el flujo neto a través de una 3-superficie quedará definida de la misma manera, como A^αn_αdS. Si en el 2-espacio tenemos que llevar a cabo una doble integración para cada sección de superficie atravesada por el campo vectorial A, en el 3-espacio tenemos que llevar a cabo una triple integración para cada 3-superficie. Si llevamos a cabo la evaluación de la integral del vector J = (J^α) sobre una superficie, entonces el flujo total cuando la integración se lleva a cabo sobre una hipersuperficie t = constante está dado por:

Obviamente, las últimas tres integrales se desvanecen al llevarse a cabo las integraciones sobre una hipersuperficie t = constante. Esto nos produce la expresión que se deseaba demostrar para la obtención de la carga eléctrica total Q en un 4-espacio relativista.

Hasta aquí hemos visto que un campo eléctrico E y un campo magnético B no poseen una existencia verdaderamente independiente ni poseen separadamente cada uno de ellos una invariancia Lorentziana, y hemos visto que ambos son a su vez meros componentes del tensor de Faraday F, el cual sí es una invariante de Lorentz, el cual es la descripción invariante de los campos electromagnéticos dentro de la Teoría de la Relatividad. Hemos analizado, desde el punto de vista relativista, lo que ocurre cuando consideramos una carga eléctrica que está en reposo en un marco de referencia y que vista desde otro marco de referencia se encuentra en movimiento. También hemos estudiado cómo una línea infinitamente larga cargada eléctricamente, si es vista por un observador moviéndose a lo largo de un eje paralelo a dicha línea, produce la inducción propia de un campo magnético B. La concordancia plena entre la electrodinámica clásica y la Teoría General de la Relatividad es algo que no se pone a discusión. Sin embargo, al tratar de extender la electrodinámica clásica hacia marcos de referencia acelerados, no tardamos en toparnos con problemas al tratar de compaginar los resultados con las conclusiones obtenidas mediante la Relatividad General para el caso del campo gravitacional. Antes de entrar en detalle sobre los problemas que confrontamos al tratar de “pegar” a la electrodinámica clásica con la Relatividad General, estudiaremos el caso de una carga eléctrica que está siendo sometida a una aceleración constante. El libro convencional “Classical Electrodynamics” de John David Jackson utilizado ampliamente para el estudio de la electrodinámica en programas de postgrado al igual que muchos otros textos inspirados en este libro adoptan la postura de que la potencia de la radiación emitida por una carga eléctrica que está siendo acelerada depende exclusivamente de la aceleración. El punto usual de partida es la definición del vector de Poynting S. No es difícil demostrar que la potencia de la energía electromagnética está dada por la siguiente fórmula conocida como fórmula de Larmor para velocidades suficientemente bajas en comparación con la velocidad de la luz:

siendo q la carga eléctrica de la partícula y siendo a = (a_x, a_y, a_z) la aceleración en coordenadas Cartesianas rectangulares. Esta fórmula tiene además la propiedad de que es una invariante de Lorentz, pese al hecho de que sólo es válida para velocidades suficientemente bajas en comparación con la velocidad de la luz.

PROBLEMA: Sin recurrir a cálculos detallados, demostrar que la fórmula de Larmor es una invariante de Lorentz que conserva su forma tras un cambio de marcos de referencia.

La potencia de la energía electromagnética que está siendo radiada por la carga eléctrica que está siendo acelerada está dada por la razón de la pérdida de energía, - dW/dt, tal y como se observa y se mide en el sistema de referencia S. Del mismo modo, en el sistema de referencia S’, la pérdida de energía está dada por - dW’/dt’. Pero W es proporcional a la primera componente del 4-vector energía-momentum (E/c, p_x, p_y, p_z), mientras que t es proporcional también a la primera componente de un 4-vector, el vector posición (ct,x,y,z), y en este caso ambas cantidades están sujetas a la misma transformación de Lorentz, con lo cual la los factores comunes de conversión Lorentziana tanto en el numerador como en el denominador se cancelan, dejándonos con la misma expresión. Se concluye que la fórmula de Larmor es una invariante de Lorentz, y puede ser escrita para el sistema de referencia S’ de la siguiente manera:

Sin embargo, tanto en el sistema de referencia S como en el sistema de referencia S’, la fórmula de Larmor es sólo válida para velocidades suficientemente bajas en comparación con la velocidad de la luz, de modo tal que la fórmula de Larmor no es covariante. El primer paso consistirá en modificar la fórmula para que ésta sea covariante, tensorial. La reformulación de la 3-aceleración a como una 4-aceleración A se puede efectuar mediante una contracción tensorial en el 4-espacio de la siguiente manera empleando la convención de sumación por la vía de los índices repetidos:

A_μA^μ

De este modo, la fórmula de Larmor covariante queda escrita del siguiente modo especificada para el 4-espacio en lugar del 3-espacio:

Esta es la fórmula de Larmor expresada en forma covariante. Pero aún no es una fórmula relativísticamente correcta. Puesto que en la fórmula original de Larmor tanto la aceleración a en el sistema de referencia S’ como la aceleración a en el sistema de referencia S son 3-aceleraciones, el paso lógico consiste en reemplazar la 3-aceleración con una 4-aceleración A = (U^α), obtenida directamente de la diferenciación con respecto al tiempo propio (local) τ de la 4-velocidad U = (U^α) empleada en la Teoría Especial de la Relatividad, la cual en nuestra introducción a los 4-vectores vimos que era igual a:

U = (U^α) = (γc, γu)

siendo u la 3-velocidad. La diferenciación de la 4-velocidad U con respecto al tiempo propio τ viene siendo entonces:

Para poder llevar a cabo la contracción tensorial de A_μ con A^μ como se indica arriba, necesitamos la forma covariante de la 4-aceleración A, la cual obtenemos con la ayuda del tensor métrico g = (g_αβ) que corresponde al espacio-tiempo Lorentziano de la Teoría Especial de la Relatividad, con lo cual obtenemos lo siguiente tras bajar el índice de A^μ:

Pero el tiempo t y el tiempo propio τ están relacionados mediante la expresión relativista para la dilatación del tiempo t = γτ. Entonces de inicio tenemos que tener algo como lo siguiente para el 4-vector velocidad U:

De este modo, tenemos lo siguiente:

Este paso anterior era necesario porque nuestro punto de partida fue una relación especificada no en el tiempo propio τ sino en el tiempo del observador externo t, y esto nos introduce un factor γ al ponerlo todo en función de los 4-vectores relativistas, algo que tenemos que agregar a la relación final que obtengamos.

Con lo que tenemos arriba, el procedimiento de desarrollo para obtener la 4-aceleración relativista que tenemos que utilizar en la versión covariante de la fórmula de Larmor es directo. El álgebra es un poco laboriosa y no será reproducida aquí. Sin embargo, una simplificación que podemos utilizar en los procedimientos algebraicos para ahorrarnos varios pasos es la siguiente:

Con lo anterior llegamos por fin a la siguiente fórmula de Larmor relativista:

El término entre los paréntesis es esencialmente un término relativista de aceleración. Podemos poner esta ecuación en una forma un poco más útil, en lo que a interpretación de resultados físicos se refiere, recurriendo a la definición del producto cruz de dos vectores especificado del siguiente modo:

y recurriendo también a la definición del producto escalar de dos vectores especificado del siguiente modo:

Con estas dos relaciones vectoriales, podemos efectuar la siguiente manipulación del término relativista dentro los paréntesis en la fórmula de Larmor:

La fórmula relativista de Larmor toma entonces la siguiente forma:

En un movimiento de aceleración lineal el 3-vector velocidad u siempre será paralelo al 3-vector aceleración du/dt, de modo tal que el segundo término dentro del paréntesis se desvanece proporcionándonos la energía electromagnética emitida por la carga acelerada moviéndose siempre en una misma dirección. Y en un movimiento en el cual el 3-vector velocidad u está cambiando de dirección constantemente, siendo perpendicular al 3-vector aceleración du/dt como ocurre en el caso de los aceleradores de partículas tales como el ciclotrón y el sincrotrón, el segundo término contribuirá a la radiación emitida, y es precisamente éste término el que pone un límite práctico a la velocidad que se le pueda imprimir a partículas atómicas y sub-atómicas en un acelerador rotatorio. Haciendo la simplificación β = u/c y metiendo la constante c² tomándola del denominador del factor externo para meterla en el primer témino dentro del paréntesis, juntándola con la otra constante c² que está en el segundo término para incorporarla del mismo modo en cada u del segundo término, tenemos otra variante de la fórmula de Larmor relativista, válida para cualquier velocidad:

PROBLEMA: Obtener una fórmula para la potencia de la energía electromagnética radiada en función del cambio de la energía cinética K de la partícula con respecto a la distancia recorrida (= dK/dx) para una aceleración lineal. Suponiendo para los aceleradores electroestáticos lineales de partículas una ganancia de 10 MeV/metro, demuéstrese que bajo tales condiciones la pérdida de energía por radiación es despreciable.

Ya hemos visto previamente en otra entradas que la energía cinética relativista K está dada por la fórmula:

K = (γ - 1) m₀c²

Tomando la derivada de K con respecto al tiempo y usando un resultado obtenido arriba tenemos entonces:

Con la ayuda de la regla de la cadena, podemos obtener dK/dx de la siguiente manera:

Despejando esto último para poner todo en función de la aceleración du/dt:

Reemplazando esto en la expresión para la potencia radiada en el caso de que la aceleración es lineal con la velocidad u y la aceleración du/dt colineares (apuntando en la misma dirección) obtenemos la expresión deseada:

Evaluaremos ahora la potencia electormagnética radiada para un valor de dK/dt = 10 MeV/metro. Podemos llevar a cabo los cálculos numéricos de una manera más elegante y menos propensa a errores escribiendo lo anterior de la siguiente manera:

Con estos cambios, en el denominador tenemos a la energía en reposo m₀c² de la partícula, que para un electrón es igual a 0.511 MeV. Y en el numerador tenemos una cantidad (q²/m₀c²) que resulta ser igual a una longitud que en este caso viene siendo el radio clásico del electrón que fue obtenido por Thomson con la siguiente fórmula en el sistema de unidades Gaussianas:

Para que esto sea cierto, tenemos que utilizar para la unidad fundamental de carga un valor de 4.8·10^-10 statcoulombs (o bien 4.8·10^-10 esu ó electrostatic unit, siendo el statcoulomb una unidad cuya conversión al sistema SI es 1 statcoulomb ≈ 3.33564×10⁻¹⁰ coulombs). Empleando valores numéricos tenemos entonces que la potencia radiada será:

{[2(2.82·10^-13 metro)(3·10¹⁰ cm/seg)]/[3(0.511 MeV)]}/{10 MeV/100 cm}²

≈ 11·10^-5 MeV/segundo

La fracción de la potencia que es perdida por radiación electromagnética para esta partícula, en este caso un electrón que suponemos que está viajando a velocidades relativistas, será entonces:

(11·10^-5 MeV/segundo)/[(10 MeV/100 cm)(3·10¹⁰ cm/seg)]

≈ 3.67·10^-14

Esta es una fracción despreciable, y tiene una consecuencia que será relevante para nuestra discusión posterior: es prácticamente imposible obtener de una partícula que está siendo acelerada linealmente información experimental que confirme la exactitud de las fórmulas relativistas para la radiación electromagnética radiada por una carga acelerada.

En realidad, hay un pequeño detalle que hemos pasado por alto con el fin de no embrollar más los cálculos teóricos. Si una partícula es acelerada produciendo con ello un campo electromagnético de radiación, el movimiento posterior de la partícula indudablemente será modificado por este campo de radiación. Este fenómeno es conocido teóricamente como reacción de radiación o amortiguamiento por la radiación (radiation damping). De cualquier manera, en lo que hemos visto acerca de cargas eléctricas y consecuentemente campos eléctricos acelerados todo hasta aquí parece ser consistente, libre de conflictos internos. Consideraremos ahora cómo empiezan a surgir dificultades en cuanto entra en el panorama la Relatividad General.

Si aceptamos en toda su extensión el principio fuerte de equivalencia de la Relatividad General, la equivalencia plena entre la gravedad y la aceleración, la sola idea de que la radiación electromagnética es una función de la aceleración de una carga eléctrica se vuelve problemática, porque bajo este contexto un objeto puede estar estacionario en el mismo lugar y acelerándose al mismo tiempo. Por ejemplo, un objeto cargado eléctricamente puede estar en reposo sobre la superficie de la Tierra, y sin embargo está sujeto también a una aceleración gravitatoria g de aproximadamente 9.8 metros/seg². Es precisamente esta aceleración gravitatoria la que ocasiona que una masa tenga peso (W = mg), y que ese peso sea menor en la superficie de un cuerpo celeste con menor atracción gravitatoria (como la Luna) o mayor en la superficie de un cuerpo celeste con mayor atracción gravitatoria (como el planeta Júpiter), siendo el peso igual a cero cuando el objeto está flotando libremente en el espacio. Podemos decir con plena certeza que un objeto que permanece estacionario sobre la superficie de la Tierra no está radiando energía electromagnética, al menos desde el punto de vista de observadores co-estacionarios. Si estuviese radiando energía electromagnética, tendríamos entonces una fuente perpetua y gratuita de energía. Puesto que la fuerza de empuje que sostiene al cuerpo en su lugar en la superficie terrestre no actúa a lo largo de distancia alguna, el trabajo hecho por esta fuerza es cero. Entonces no se está metiendo energía alguna en el objeto, de modo tal que si el objeto estuviese emitiendo energía electromagnética (y suponiendo que la energía interna del objeto permanece constante) tendríamos una violación del principio de la conservación de la energía.

Naturalmente, podríamos poner en tela de duda la aserción de que no se está haciendo trabajo alguno por la fuerza de empuje que mantiene al objeto en la superficie de la Tierra. Si imaginamos una cápsula herméticamente sellada en caída libre, y si dentro de dicha cápsula un objeto se está acelerando (hacia arriba) de forma tal que mantiene la misma altura relativa en relación a la fuente gravitatoria externa, podríamos decir que dentro de la cápsula hemos estado haciendo un trabajo sobre el objeto al ir aumentando su velocidad (hacia arriba) dentro de la cápsula, relativa a la cápsula misma, pese a que desde el punto de vista (externo) de la fuente gravitatoria (la Tierra) el objeto permanece estacionario y no se ha efectuado trabajo alguno sobre el objeto. Esto no debe sorprendernos, puesto que el trabajo y la energía cinética son entendidos como conceptos relativos, pero nos conduce a la conclusión inusual de que la radiación electromagnética también debe ser un concepto relativo. La relatividad que ya nos debe ser familiar de la energía cinética se corresponde con la simetría que hay entre marcos de referencia distintos, es decir, siempre podemos encontrar un marco inercial (Lorentziano) de referencia con respecto al cual cualquier objeto (en un instante dado) tiene una energía cinética igual a cero por estar el objeto instantáneamente en reposo en dicho marco de referencia que hemos llamado el marco de referencia comóvil. El considerar partículas cargadas eléctricamente en presencia de un campo gravitacional parece sugerir de igual modo que siempre podemos encontrar un sistema de coordenadas (al menos localmente) con respecto al cual un objeto cargado eléctricamente no emite radiación electromagnética alguna en un instante dado, aunque la partícula pueda estar emitiendo radiación electromagnética con respecto a otro sistema de coordenadas.

También podemos cuestionar el hecho de que las ecuaciones de la electrodinámica realmente impliquen el hecho de que una carga eléctrica que se esté acelerando necesariamente deba radiar energía electromagnética. Sorprendentemente, este asunto es un asunto que no se ha zanjado del todo en la teoría clásica del electromagnetismo. La dificultad radica en saber cómo poder dilucidar la influencia de una partícula cargada eléctricamente sobre sí misma. Recordemos aquí que dos electrones se repelen el uno al otro con una fuerza que es estáticamente proporcional al recíproco de la distancia que hay entre las cargas. Esto es entendido tradicionalmente como la interacción de cada partícula con el campo eléctrico de la otra partícula. La intensidad del campo eléctrico producido por cada carga aumenta hasta el infinito conforme la distancia hacia la carga se aproxima a cero (suponiendo cargas puntuales, algo que la Mecánica Cuántica considera insostenible). Pero es aquí en donde encontramos una dificultad conceptual, porque de acuerdo con esta descripción todo electrón está situado precisamente en un lugar en donde existe una fuerza de repulsión infinitamente grande en contra de los electrones.

Podemos intentar manejar esto último de varias maneras. La solución más simplista consiste simplemente en proclamar que un electrón no interactúa de modo alguno con su propio campo eléctrico, y cuando interactúa lo hace con los campos de otras partículas. Si adoptamos éste punto de vista, tenemos que explicar entonces el por qué una partícula cargada eléctricamente opone una mayor resistencia a cambios en su estado de movimiento que una partícula sin carga eléctrica alguna pero con la misma masa inercial. El análisis tradicional de las cargas aceleradas nos dice que ésta “fuerza de reacción de radiación” aplicada a lo largo del movimiento de la carga acelerada es la que nos proporciona el suministro de energía que es emitida en la forma de ondas electromagnéticas. Tradicionalmente se ha explicado que esta fuerza tiene su origen en la interacción de la partícula con su propio campo eléctrico. Por lo tanto, si proclamamos que las partículas cargadas eléctricamente no interactúan con su propio campo, entonces tenemos que buscar una explicación alterna a la reacción de radiación. Un candidato para tal cosa es la teoría del absorbedor Wheeler-Feynman, la cual empieza con la idea de que toda solución válida a las ecuaciones del campo electromagnético tiene que ser simétrica con respecto a la inversión del tiempo (t → - t), como lo son las mismas ecuaciones del campo electromagnético, siendo la motivación para dicha propuesta la importancia que la simetría del tiempo tiene en el estudio de la física, y de acuerdo con la cual la resistencia adicional presentada por una partícula cargada a cambios en su estado de movimiento se debe a ondas avanzadas emanando hacia atrás en el tiempo de un conjunto de absorbedores en el futuro, cuyas ondas son excitadas por las ondas retardadas emanando de la partícula hacia adelante en el tiempo. El problema con esta explicación es que pone en aprietos al principio básico de la causalidad de la ciencia.

También podríamos argumentar que aunque la fuerza de repulsión sobre una partícula cargada producida por su propio campo es infinita, ésta debe ser igualmente infinita en todas las direcciones posibles, de modo tal que las fuerzas infinitas se cancelan dejando una fuerza neta de cero sobre la partícula debida a su propio campo, al menos si la partícula está en movimiento uniforme. Podemos suponer además que la aceleración de una partícula cargada altera esta situación singular al irse sobreponiendo a su propio campo, ocasionando por lo tanto una fuerza neta. La misma perturbación del campo nos produce una radiación, de modo tal que observamos una correlación entre radiación y reacción. Sin embargo, este argumento nos lleva demasiado pronto a conclusiones que desafían nuestra intuición, empezando por el hecho de que la ecuación de movimiento que se obtiene basada en esta premisa implica que una carga eléctrica que se está acelerando no emite radiación alguna. A esto se le llama generalmente movimiento hiperbólico, porque la línea del mundo de la partícula en un diagrama espacio-tiempo de Minkowski resulta ser una hipérbola asintótica al cono de luz. Aún más perturbador resulta el hecho de que las ecuaciones de movimiento para una partícula cargada basadas sobre estas consideraciones poseen soluciones de fuga (runaway) en las cuales la partícula se acelera rápidamente hacia la velocidad de la luz. El que estas soluciones puedan ser reales o no sigue siendo motivo de debate, pero la ausencia de radiación predicha para el movimiento hiperbólico ha sido citada algunas veces como una forma de reconciliar el Principio de Equivalencia de la Relatividad General con el hecho de que una partícula cargada eléctricamente en reposo sobre la superficie de la Tierra no emite radiación electromagnética pese a que está experimentando una aceleración propia (local) de 9.8 metros/seg². En la obra Feynman Lectures on Gravitation, Richard P. Feynman va tan lejos como para afirmar que “hemos heredado el prejuicio de que una carga que se está acelerando debe emitir radiación” (Feynman fue un científico prolífico ganador del Premio Nobel que dió un gran impulso al campo de la electrodinámica cuántica o QED - Quantum Electrodynamics), y tras hacer esta aserción argumentó que la fórmula clásica que nos proporciona la potencia radiada por una carga que se está acelerando como proporcional al cuadrado de la aceleración “nos ha separado del camino correcto” porque ésta fórmula se aplica únicamente a movimientos cíclicos o acotados como los que se llevan a cabo en los aceleradores de partículas, afirmando que el trabajo hecho por unidad de tiempo en contra de la “fuerza de reacción de radiación” por una partícula que se está moviendo a lo largo del eje-x es:

De acuerdo con esta fórmula, la fuerza de reacción de radiación (y por lo tanto la potencia radiada) es proporcional a la tercera derivada de la posición, de forma tal que si la partícula se está moviendo con una aceleración constante (con lo cual d³x/dt³ = 0) entonces la partícula no emite radiación electromagnética alguna. Pero si esto es cierto, ¿entonces por qué estamos acostumbrados a considerar a la radiación estrictamente como una función de la aceleración? Feynman señala que la ecuación puede ser escrita de la siguiente manera:

en donde podemos reconocer en el primer término a la fórmula de Larmor para la potencia radiada. Para un movimiento ondulatorio senoidal sencillo x(t) = sen(wt), el primer término es proporcional a w⁴sen²(wt), el cual es definitivamente positivo (positive definite) mientras que el segundo término es proporcional a w⁴cos(2wt) que oscila por intervalos de tiempo iguales entre valores positivos y negativos. Con esto, el trabajo acumulativo integrado representado por el segundo término sobre cualquier número entero de cicles es igual a cero, mientras que el trabajo representado por el primer término aumenta paulatinamente. Esto explica el por qué usualmente ignoramos el segundo término y tomamos el primer término como la definición de la potencia electromagnética radiada, lo cual nos lleva a la conclusión errónea de que la radiación es estrictamente una función de la segunda derivada (aceleración), cuando de hecho es proporcional a la tercera derivada de la posición. (Dicho sea de paso, si regresamos a la ecuación original anterior aplicándola a nuestra partícula sinusoidal, obtenemos una potencia que es proporcional a w⁴cos²(wt), lo cual demuestra que el efecto del término que no es definitivamente positivo en la segunda ecuación equivale a desplazar la fase de la potencia por un ángulo de π/2.

Pese a las correcciones hechas por Feynman, no existe un acuerdo general en la literatura acerca de si una carga acelerada uniformemente es capaz de radiar en el ámbito de la electrodinámica clásica, e inclusive mucha gente rechaza las conclusiones de Feynman como absurdas. A modo de ejemplo, en el libro “Electromagnetic Fields and Interactions” de Richard Becker encontramos en el párrafo 4 de la Parte II el argumento de que la ecuación de Feynman es válida únicamente para movimientos casi periódicos para los cuales todas las derivadas de la posición son proporcionales a las potencias correspondientes de las frecuencias, señalando que “se obtienen resultados absurdos si (la ecuación de Feynman) es aplicada a otros tipos de movimiento, tales como el retardamiento de un electrón libre en un campo eléctrico que se opone a su avance. En este caso, sólo la segunda derivada será diferente de cero, y la ecuación no será capaz de predecir ningún amortiguamiento ocasionado por la radiación (esto es conocido en los textos de la electrodinámica clásica como radiation damping). La derivación dada arriba del amortiguamiento de la radiación no es satisfactoria, porque no está claro cómo la onda esférica que es emitida influye en el movimiento del electrón. Para poder lograr un entendimiento más cercano sobre la naturaleza de esta ‘auto-reacción’ es necesario calcular la fuerza resultante sobre todos los elementos de volumen del electrón. Tipos de movimiento (tales como el del electrón libre) sólo pueden ser tratados a la luz de un conocimiento más preciso de la estructura del electrón”. De este modo, Becker rechaza como absurda la noción de que una carga en movimiento uniformemente acelerado no experimenta reacción de radiación, mientras que Feynman defiende su propuesta basándose en el Principio de Equivalencia de la Relatividad General.

Naturalmente, sabemos que arriba de cierta frecuencia (o debajo de cierta longitud de onda, que viene siendo el enunciado equivalente) las ecuaciones clásicas del electromagnetismo dejan de ser válidas:

como lo muestra el contraste entre la conclusión matemática clásica de la “catástrofe del ultravioleta” proveniente del análisis de una radiación de cavidad y los resultados obtenidos experimentalmente. El efecto fotoeléctrico debe ser tomado en cuenta también al igual que todos los demás efectos de naturaleza mecánico-cuántica, los cuales son incompatibles con la concepción ondulatoria sencilla de la radiación electromagnética. De cualquier modo, aún en la teoría cuántica de la electrodinámica encontramos que el asunto de la reacción de radiación nos conduce a dificultades que hasta la fecha sólo han podido ser resueltas de una manera ad hoc mediante el proceso matemético de renormalización.

Resulta interesante considerar el resultado de tratar a la radiación electromagnética simplemente como la emisión de partículas clásicas moviéndose a velocidad constante, muy al estilo de la teoría corpuscular de Newton. Aquí encontramos de inmediato dificultades, porque estos corpúsculos de luz son portadores de momentum, y si se considera que son emitidos de manera discreta (en “cuantos”) por la partícula cargada, entonces la reacción debería ser un impulso, lo cual implica una aceleración de la partícula emisora, aunque de una duración infinitesimalmente pequeña de tiempo. Ahora bien, si la radiación electromagnética proveniente de esta partícula es estrictamente proporcional a la aceleración, debemos esperar que la partícula esté radiando a una razón infinita por un un período infinitesimalmente pequeño de tiempo debido a la reacción de la emisión de un solo corpúsculo de radiación. Podría argumentarse que el monto total (integrado) de esta radiación es finito, pero la emisión de cada uno de estos corpúsculos radiados le dá un impulso adicional de aceleración a la partícula cargada eléctricamente, resultando a su vez en más radiación, y así sucesivamente. Esto nos demuestra claramente la naturaleza problemática de las proposición dual de que la aceleración produce radiación y de que la radiación provoca aceleración. Resulta obvio que estas dos proposiciones deben ser balanceadas cuidadosamente para poder producir resultados bien comportados.

En el pasaje introductorio de su primer trabajo publicado en 1905 sobre la Teoría de la Relatividad titulado “Sobre la electrodinámica de los cuerpos en movimiento”, Einstein usa como paradigma el movimiento relativo entre un conductor y un imán moviéndose a una velocidad constante, destacando que es el movimiento relativo entre ambos lo que produce el fenómeno de inducción, sin hacer referencia alguna a ningún tipo de radiación electromagnética, destacando también que el tratamiento clásico pre-relativista (basado en las transformaciones de Galileo) conduce a asimetrías que no están presentes en los fenómenos de la electrodinámica. Hoy nos encontramos en una situación parecida a la que encontró Einstein al tratar de liberar a la electrodinámica clásica de su tiempo de dichas asimetrías si intentamos extender la filosofía relativista a cargas que están siendo aceleradas, porque si hacemos tal cosa nos topamos nuevamente con la existencia de asimetrías que no son parte inherente de los fenómenos bajo observación, especialmente si aceptamos plenamente la versión fuerte del Principio de Equivalencia de la Relatividad General. Si sometemos a una partícula cargada a un movimiento acelerado periódico mientras un conductor distante está en reposo o en movimiento a velocidad constante, la partícula cargada emitirá radiación electromagnética con momentum y energía bien definidos por la electrodinámica clásica, y esta radiación inducirá corrientes pequeñas en el conductor. Por otro lado, si es la partícula la que está en reposo o en movimiento uniforme mientras que el conductor distante es sometido a un movimiento oscilatorio acelerado, no habrá radiación electromagnética emanada de la carga (de acuerdo con el punto de vista tradicional) aunque de cualquier manera aparecerán corrientes en el conductor, ahora atribuídas al campo eléctrico estático. Parece razonable sugerir que no es justificable la distinción trazada por el punto de vista tradicional sobre las dos circunstancias mencionadas, y el principio de la relatividad debe poder ser aplicado a las descripciones de efectos físicos con respecto a sistemas de referencia mucho más generales. Esto es en efecto lo que abarca la versión fuerte del Principio de Equivalencia, y es la razón por la cual Einstein consideró a su teoría de la gravedad como una generalización y extensión del principio de la relatividad. En 1917 Einstein escribió lo siguiente: “De acuerdo con esta concepción, uno no puede hablar de la aceleración absoluta de un sistema de referencia, del mismo modo que en la Teoría de la Relatividad uno no puede hablar de la velocidad absoluta de un sistema”. Sin embargo, no todos están de acuerdo con esta observación fundamental hecha por Einstein, entre ellos Hans Ohanian y Remo Ruffini, los cuales en su libro “Gravitation and Spacetime” escriben: “Resulta tentador darle al principio de invariancia general la interpretación física de que la aceleración también es relativa. Einstein llamó a su teoría de la gravedad la teoría de la relatividad general porque él pensaba que (localmente) los fenómenos observados en un campo gravitacional son indistinguibles de aquellos fenómenos observados en un sistema acelerado de referencia. Sin embargo, los efectos de marea (estos no tienen nada que ver con la marea que provoca la Luna en el nivel del mar en los puertos, son consecuencia del hecho de que las trayectorias de dos cuerpos en caída libre convergen hacia un mismo punto cuando son extendidas) nos permiten establecer una distinción clara entre las fuerzas gravitacionales y las pseudo-fuerzas encontradas en los marcos acelerados de referencia. Por lo tanto es falso hablar de una relatividad general del movimiento”. La respuesta dada por los relativistas teóricos a este argumento es que en primer lugar la teoría de Einstein no es propiamente hablando la teoría de la relatividad general, sino una teoría general de la relatividad, y en segundo lugar la idea de que los efectos de marea falsifican el Principio de Equivalencia es incorrecta, la cual surge del fallo en reconocer que la restricción de localización es tanto temporal como espacial y que, más aún, aquellos que suponen que la “gravedad verdadera” sólo existe en donde hay una curvatura local del espacio-tiempo, yerran en considerar circunstancias en las cuales se puede producir un campo gravitacional perfectamente uniforme sobre una región limitada mediante un arreglo adecuado de materia; ¿podrían realmente argumentar que no hay gravedad verdadera en tal región sólo porque no hay una curvatura local? En este respecto, el Principio de Equivalencia no es más que la versión en el espacio-tiempo de la proposición de la geometría Riemanniana de que una “hoja” diferenciable es localmente Euclideana (esto lo iremos viendo con mayor detalle en entradas posteriores).

Una de las bases de nuestro prejuicio de que la radiación electromagnética debe ser absoluta es la noción de que la radiación está formada por esas entidades discretas identificables y localizables que llamamos fotones, desligadas en el curso de su existencia tanto de sus entidades emisoras como de las entidades que las absorben. Este modo de pensar es lo que ha llevado a mucha gente a aceptar ciegamente la existencia del “fotón libre”, aunque de acuerdo a nuestra experiencia en realidad tal cosa no existe, ya que un fotón es necesariamente emitido y absorbido. De no ser así, no tendríamos conocimiento de su existencia. Los únicos eventos que son directamente observables son la emisión y la absorción del fotón, no la existencia de alguna entidad “en tránsito”. Esto está relacionado directamente con la imposibilidad de la existencia de una onda electromagnética perfectamente monocromática (“vibrando” a una sola frecuencia fija):

porque para que ésta sea perfectamente monocromática no debe tener principio ni fin. Si consideramos puntos de inicio y terminación como necesariamente tiene que ocurrir con los fotones de luz:

esto nos introduce componentes de frecuencia adicionales de acuerdo a lo que nos dice la teoría matemática conocida como el análisis de Fourier. Inclusive es dudoso que ésta última representación sea la que más aproxima a la realidad física, y la representación de un cuanto de onda electromagnética podría ser también la siguiente (entre muchas otras posibles):

Se debe recordar también que una onda perfectamente monocromática no es portadora de información alguna, y por lo tanto no está sujeta a limitación alguna de esa característica física que llamamos su velocidad de fase. Usualmente consideramos que la limitación relativista impuesta por la velocidad de la luz se aplica tanto a la energía como a la información, de modo tal que esto plantea la interrogante filosófica de que algo que sea perfectamente monocromático (si es que tal cosa realmente exista) pueda ser portador de energía alguna. Muchos de los que han estudiado este asunto a fondo enfatizan la distinción que debe de haber entre una carga eléctrica que ha sido uniformemente acelerada para todo el tiempo y una carga eléctrica que ha sido acelerada por un período prolongado de tiempo pero finito. Ultimadamente esto tiene una conexión con la distinción que pueda haber entre un fotón libre (si es que tal cosa existe) y un fotón real que es necesariamente emitido y absorbido.

Otro punto de vista lo encontramos en el libro “Electrodynamics and Classical Theory of Fields and Particles” de Asim Orhan Barut, publicado en 1964 y nuevamente en 1980, en el cual lleva a cabo una derivación de la fuerza de reacción de radiación empleando como punto de partida un simple balance de energía basado en la premisa de que la potencia electromagnética, considerada como energía por unidad de tiempo, está dada por la fórmula de Larmor. Igualando la integral de esta potencia electromagnética con la integral del producto de la fuerza de reacción de radiación por la velocidad tenemos el siguiente enunciado (estamos utilizando aquí la notación del punto puesto encima de la variable para indicar la derivada con respecto al tiempo de la variable, y un doble punto para indicar la segunda derivada con respecto al tiempo de la variable):

Haremos uso de la siguiente igualdad:

la cual a su vez implica lo siguiente:

De este modo, si seleccionamos un intervalo de tiempo {0,T} tal que la primera o la segunda derivada sea cero en ambos extremos de la integral, entonces el primer término en el lado derecho de esta expresión se desvanece, lo cual nos permite substituír esto en la ecuación del “balance de energía” y reacomodar los miembros bajo un solo símbolo integral para obtener así:

Tras esto, Barut hace la observación de que una solución (aunque no necesariamente la única) de esta última expresión se obtiene fijando el integrando a cero, obteniéndose así:

De este modo, hemos llegado a la fórmula original de Feynman, aunque aquí está ocurriendo algo inusual, porque Feynman empezó su análisis con esta relación argumentando que es aplicable a movimientos generales, tras lo cual derivó la ecuación de Barut para el “balance de energía” como una aproximación al movimiento periódico. En contraste, Barut empezó con su igualdad para el “balance de energía” defendiendo su validez para movimientos generales, tras lo cual derivó la ecuación original de Feynman como una aproximación para un movimiento periódico, precisamente el reverso del razonamiento de Feynman. Como si esto no fuese ya de por sí suficientemente confuso, Barut concluye diciendo que: “La suposición hecha arriba de que d²x/dt² se desvanece en t = 0 y en t = T es ciertamente verdadera para el movimiento oscilatorio, pero esperamos que un resultado como la ecuación (5) deba ser generalmente cierto”. Desafortunadamente, no entra en detalle del por qué deberíamos esperar ésto. Casi todos parecen invocar la identidad:

pero no parece haber un consenso común sobre cómo deba interpretarse, y sobre qué términos deba considerarse fundamental.

Mucha de la literatura sobre el asunto de la radiación proveniente de cargas aceleradas se enfoca en la ecuación del movimiento Lorentz-Dirac interactuando tanto con un campo externo como con su propio campo. Esta ecuación es el origen de la ecuación de Feynman, pero es importante recordar que está basada en la electrodinámica clásica de partículas puntuales en vez de estar basada en la electrodinámica cuántica, de modo tal que su relevancia física es cuestionable. El mismo principio de incertidumbre de Heisenberg descarta cualquier posibilidad de existencia de una partícula puntual porque de ser así, no habría límite alguno, ni siquiera teórico, para la ubicación de una carga eléctrica con un grado ilimitado de precisión, lo cual sabemos ya que no es posible en virtud de la naturaleza ondulatoria de la materia. Más aún, la validez de la ecuación Lorentz-Dirac es puesta en entredicho debido a la existencia de soluciones de fuga para la misma que presumiblemente no son observadas en el laboratorio, aunque sería interesante considerar como podría comportarse una partícula de fuga. El problema fundamental es que, aunque esta ecuación involucra la tercera derivada de la posición, no podemos especificar plenamente las condiciones iniciales únicamente en términos de la posición y la velocidad como podemos hacerlo para las ecuaciones ordinarias del movimiento. En la mecánica teórica, el espacio fase (phase space) usual para N partículas tiene 6N dimensiones (tres coordenadas para la dimensión y tres coordenadas para el momentum de cada partícula), mientras que el espacio fase para una partícula cargada bajo la ecuación de Lorentz-Dirac tendría 9N dimensiones. Típicamente, consideramos a la posición y a la velocidad (o el momentum) como parámetros independientes libres, en el sentido de que cualquier sistema físico puede ser postulado como residente en cualquier punto de ese espacio fase, tras lo cual irá evolucionando de acuerdo a las leyes del movimiento. Sin embargo, ya no es tan claro el que la posición, la velocidad, y la aceleración puedan ser considerados en el mismo sentido como parámetros libres mutuamente independientes. Las ecuaciones de campo de la Relatividad General proporcionan una buena ilustración de cómo leyes que son no-lineares implican restricciones (tales como las identidades de Bianchi) sobre las condiciones iniciales permisibles, de modo tal que no estamos libres de poder especificar un sistema en un punto arbitrario del espacio fase. Este tipo de restricción es aplicable también a la ecuación Lorentz-Dirac, puesto que ésta ecuación también es no-linear. Sin embargo, la existencia de soluciones de fuga (presumiblemente irreales) nos indica un tipo más sutil de restricción sobre las condiciones iniciales permisibles. Los puntos permisibles en el espacio fase no sólo deben satisfacer las restricciones instantáneas, también deben ser (evidentemente) tales que nunca terminen evolucionando hacia regiones singulares o irreales del espacio fase. Por otro lado, el desprecio usual al campo estático “cercano” al estar analizando el campo de radicación “lejano” está basado en la suposición de que la distancia r a la fuente es lo suficientemente grande como para que términos proporcionales a 1/r² sean despreciables en comparación con los términos proporcionales a 1/r, aunque los cálculos de la reacción de radiación se extienden hasta r = 0. De cualquier manera, pese a la posición y fisicalidad dudosa de la ecuación Lorentz-Dirac, es instructivo repasar brevemente la forma de ésta ecuación así como sus implicaciones. Después de la re-normalización de la masa, y utilizando para la velocidad de la luz un valor igual a la unidad con fines de simplificación, esta ecuación para una partícula de masa m y carga q se puede escribir de la manera siguiente:

en donde U es la 4-velocidad, A es la 4-aceleración, F es la 4-fuerza de Minkowski (con los componentes F^m = F^m_nu^m debidos a un campo externo F^m_n), τ es el tiempo propio a lo largo de la línea del mundo de la partícula (en el diagrama espacio-tiempo de Minkowski), mientras que A² es el invariante escalar obtenido de la contracción del vector A consigo mismo. El primer término en el lado derecho es la fuerza de Lorentz, y el segundo término es la fuerza de reacción de radiación. Para nuestros propósitos, el aspecto más interesante de esta ecuación es el hecho de que la fuerza de radiación se desvanece si la aceleración propia A de la partícula es constante. En otras palabras, la cantidad dentro de los paréntesis es igual a cero bajo estas condiciones. El desvanecimiento de la cantidad entre los paréntesis puede ser expresado de la siguiente manera (la derivada de la 4-aceleración se toma aquí como la segunda derivada de la 4-velocidad):

La condición de una aceleración propia constante implica que el cuadrado de la magnitud de la 4-aceleración sea también constante, igual al negativo del cuadrado de la magnitud a² del 3-vector a con respecto al marco de referencia co-móvil instantáneo. Por lo tanto, la fuerza de reacción de radiación se desvanece (para una carga diferente de cero) sí y solo sí el 4-vector velocidad satisface la ecuación harmónica:

El movimiento debe ser a lo largo de una línea recta, de modo tal que podemos considerar únicamente un movimiento a lo largo del eje-x con un tiempo de coordenada t, en cuyo caso ésta ecuación implica lo siguiente al considerar el primer componente (temporal, que aquí identificaremos con el índice cero como se acostumbra hacerlo en muchos textos) y el segundo componente (espacial, a lo largo del eje-x, que aquí identificaremos con el índice 1):

en donde U₀ = dt/dτ y U₁ = dx/dτ. Una solución de este par de ecuaciones es la siguiente:

que representan las ecuaciones familiares de “movimiento hiperbólico”, movimiento con una aceleración propia constante. Esta es la base para la propuesta de que una carga uniformemente acelerada no es capaz de emitir radiación electromagnética alguna, porque la energía de radiación presumiblemente viene del trabajo efectuado en contra de la fuerza de reacción de radiación, el cual es igual a cero para un movimiento con aceleración propia constante, al menos de acuerdo con la ecuación Lorentz-Dirac. Sin embargo, como ya se ha señalado con anterioridad, esta ecuación está fincada sobre suposiciones cuestionables, y se sabe que posee soluciones dudosas, de las cuales las más problemáticas son las soluciones de fuga. Para una partícula cargada eléctricamente, la ecuación Lorentz-Dirac se reduce a:

Enfocándonos nuevamente a un movimiento a lo largo del eje-x, esta ecuación vectorial puede ser descompuesta en sus componentes esenciales, el primero de los cuales es:

teniendo la condición hiperbólica U₀² - U₁² = 1, y una forma de asegurar automáticamente esta condición consiste en fijar:

U₀(τ) = cosh{f(τ)}____U₁(τ) = senh{f(τ)}

para alguna función arbitraria f. Insertando estas dos relaciones en la ecuación anterior, tenemos entonces:

Dividiendo lo último entre senh(f) llegamos a lo siguiente:

Integrando esto dos veces tenemos entonces:

en donde C = (2q²)/(3m₀) y los símbolos k y J representan constantes arbitrarias de integración. El componente U₁ de la ecuación Lorentz-Dirac nos lleva a las mismas condiciones para f (los componentes U₂ y U₃ son desde luego satisfechos con U₁(τ) = U₂(τ) =0), de modo que haciendo K = kC una solución de la ecuación Lorentz-Dirac para movimiento a lo largo del eje-x en la ausencia de fuerza alguna se puede escribir como:

Por lo tanto la velocidad de la partícula con respecto a las coordenadas (t,x) viene siendo:

La tangente hiperbólica es asintótica a ±1, de modo tal que dependiendo del signo de K la velocidad de la partícula se aproxima rápidamente a la velocidad de la luz conforme el tiempo t aumenta. Estas soluciones de fuga (conocidas también como soluciones “auto-aceleradas”) son consideradas generalmente como carentes de significado físico, poniendo en entredicho la validez de la ecuación de movimiento Lorentz-Dirac. Es interesante observar que estas soluciones no son simétricas en el tiempo, porque la constante C = (2q²)/(3m₀) es definitivamente positiva (presumiblemente). Por lo tanto, la partícula libre con carga eléctrica se aproxima a la velocidad de la luz en la dirección positiva de t, mientras que en la dirección negativa de t se aproxima a una velocidad fija tanh(J). Estas soluciones serían simétricas (en el tiempo) solo si q² o m₀ pudieran ser negativos. Las rarezas de estas soluciones de fuga han llevado a una inspección más cuidadosa de las premisas sobre las cuales se basa la ecuación Lorentz-Dirac. Existen diferencias sutiles de interpretación cuando se intenta igualar la energía de la radiación electromagnética emitida por una partícula con el trabajo hecho sobre la partícula, y esto sin mencionar la dificultad en intentar aislar la masa inercial m de la “masa” electromagnética (por ejemplo, si nos preguntamos si una partícula cargada eléctricamente requiere la misma fuerza de empuje hacia arriba para mantenerla estacionaria sobre la superficie de la Tierra que una partícula con la misma masa pero sin carga eléctrica, tenemos que considerar cuidadosamente cómo la carga eléctrica puede contribuír a la masa de la partícula. Como resultado de estas consideraciones, la ecuación Lorentz-Dirac no nos proporciona una respuesta sobre si una carga eléctrica uniformemente acelerada es capaz de emitir radiación electromagnética.

En síntesis, aunque la electrodinámica clásica Maxwelliana que inspiró a Einstein parece tener una concordancia excelente con la Teoría Especial de la Relatividad, a la hora de considerar cargas eléctricas aceleradas empezamos a ser acosados con dificultades de difícil resolución. Una parte de estas dificultades se pueden sobrellevar dando el salto de la eletrodinámica clásica a la electrodinámica cuántica. Pero el panorama está notoriamente incompleto en virtud de que al considerar movimientos acelerados de cuerpos con masa, no tenemos hasta el momento algo que nos permita transitar de la Teoría de la Relatividad hacia una Teoría Cuántica de la Relatividad, lo cual tiene a su vez un impacto directo sobre la misma electrodinámica cuántica al considerar que bajo una teoría cuántica de la gravedad el campo electromagnético debe ser capaz de interactuar con el campo gravitacional pudiéndose predecir nuevos fenómenos que hasta el momento permanecen fuera de nuestras capacidades predictivas. Una teoría cuántica de la gravedad debe ser capaz, en principio, de poder unificar plenamente la masa inercial de una partícula con su “masa” eléctrica que tradicionalmente hemos identificado como la carga eléctrica de la partícula, y aunque tradicionalmente se han manejado como dos propiedades diferentes de la misma partícula resulta obvio que ambas “masas” deben estar unificadas de un modo fundamental que está eludiendo a nuestras mejores mentes. Esta unificación (de la cual la unificación de la carga eléctrica con la masa inercial no es más que parte del asunto) era precisamente lo que buscaba Einstein en su búsqueda de un gran “campo unificado”, tarea en la cual fracasó quizá porque tal unificación requiere de una perspectiva nueva, de una forma nueva e imaginativa de pensar y ver las cosas que resulta difícil de adoptar y asimilar del mismo modo en que la propia Teoría de la Relatividad encontró dificultades en su aceptación por varias décadas. O quizá lo que nos hace falta es el desarrollo de nuevas técnicas matemáticas que nos permitan “soldar” el determinismo causalístico de la Teoría de la Relatividad con la naturaleza probabilística de la dualidad onda-partícula de la materia, técnicas matemáticas que nos permitan utilizar e inclusive ampliar lo que ya tenemos a la mano sin necesidad de tener que desmoronar todo el edificio como lo hizo Einstein con la mecánica de Newton. O quizá nos hacen falta ambas cosas. Mientras no tengamos tal teoría y tales técnicas a la mano, parece que en contra del optimismo exagerado manifestado por algunos científicos de prestigio en el sentido de que está cercano el momento de que en la física muy pronto ya no habrá nada nuevo por descubrir al contar con la Teoría del Todo parece carecer de justificación. El campo sigue abierto para todos, especialmente para las nuevas generaciones. De cualquier modo, aún con las limitaciones teóricas ya señaladas, se siguen produciendo trabajos interesantes en el campo de la electrodinámica relativista asociada a la Relatividad General, entre los cuales se puede mencionar un trabajo de Amos Harpaz titulado “An electric field in a gravitational field” (publicado en arXiv) en el cual se analiza el comportamiento de un campo eléctrico en un campo gravitacional, encontrándose que debido a la masa (energia) del campo eléctrico éste queda sometido a la acción de la gravedad, y su caída introduce una curvatura en el campo gravitacional, creando una fuerza de reacción o fuerza de tensión (stress force), teniendo como consecuencia el hecho de que la interacción de esta fuerza de reacción con la carga eléctrica estática dá origen a la emisión de radiación. En pocas palabras, un campo eléctrico por sí solo es capaz de emitir radiación electromagnética cuando es sometido a un campo gravitacional (sin embargo, la emisión sólo puede ocurrir mientras el campo eléctrico se ajusta al campo gravitacional y no después, ya que de otra manera tendríamos una fuente gratuita y perpetua de energía en violación de los principios ya conocidos). Otro trabajo interesante es el de James M. Nester y Chung-Ming Ko titulado “An accelerated charge is also absorbing power” (también publicado en arXiv) en el que repiten una conclusión que es frecuentemente pasada por alto: el que una carga eléctrica acelerada no sólo está emitiendo energía, sino que también la está absorbiendo a una razón igual a la razón de la potencia radiada predicha por la fórmula de Larmor, apoyando una propuesta presentada previamente por Jerzy Kijowski. Todos estos trabajos, desde luego, están expuestos a una revisión profunda en el momento en que podamos tener en nuestras manos una teoría que unifique plenamente a la Teoría Especial de la Relatividad y a la Relatividad General con la electrodinámica; mientras tanto hay que seguir trabajando con lo que ya se tiene.