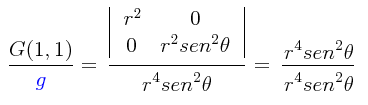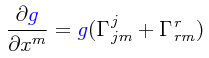Al determinante de una matriz A frecuentemente se le simboliza como |A|.
La primera vez que la mayoría de los estudiantes en las escuelas de enseñanza media y superior entran en contacto con el concepto del determinante es en la resolución de sistemas de ecuaciones lineales de primer grado, con un procedimiento de solución como el generalmente conocido como la regla de Cramer. La fórmula dada arriba para la expansión de Laplace no siempre es dada a los estudiantes en su primer contacto con el concepto del determinante, aunque la idea detrás de la fórmula les es enseñada intuitivamente.
Intuitivamente, la idea detrás de la expansión de Laplace consiste en seleccionar todo un renglón o toda una columna de una matriz A que será usado para llevar a cabo la expansión de Laplace. (En la fórmula dada arriba para la expansión de Laplace, se ha supuesto que se ha seleccionado un renglón i de la matriz, el cual es un índice libre. En caso de que se seleccione una columna, basta con especificar la sumatoria para una columna j de la matriz, reemplazándose el índice j por el índice i en la sumatoria). Para cualquier elemento que forme parte del renglón (o de la columna) seleccionado, si borramos todo el renglón y toda la columna en la que está situado obtenemos una sub-matriz llamada matriz menor aij que a su vez será manejada como un determinante det aij. Esta matriz menor, multiplicada por un signo positivo o negativo dependiendo del renglón y de la columna, recibe el nombre de cofactor.
A continuación tenemos un ejemplo de un determinante derivado de una matriz 3x3 en el cual se ha llevado a cabo una expansión de Laplace usando para dicha expansión la primera columna (obsérvese la alternancia de signos):
Y a continuación tenemos una expansión de Laplace efectuada en base al primer renglón del determinante de la matriz mostrada:
Obsérvese que los signos positivos y negativos de los cofactores aparecen mostrados en la matriz de signo puesta en la esquina superior derecha. Cada signo está dado de acuerdo con la fórmula dada arriba para la expansión de Laplace. Así, al menor M23 que corresponde al elemento puesto en el segundo renglón y en la tercera columna le tocará un signo negativo:
(-1) i + j = (-1) 2 + 3 = (-1) 5 = -1
mientras que a un menor M24 que corresponda al elemento de una matriz 6x6 puesto en el segundo renglón y en la cuarta columna le tocará un signo positivo:
(-1) i + j = (-1) 2 + 4 = (-1) 6 = + 1
Para el ejemplo numérico mostrado, el valor del determinante en base a la expansión de Laplace será:
det(A) = (+1)(-1)[4-9] + (-1)(2)[-6+2] + (+1)(0)[27-4]
det(A) = 5 + 8 + 0
det(A) = 13
det(A) = 5 + 8 + 0
det(A) = 13
No es difícil demostrar que el determinante de una matriz tiene el mismo valor independientemente del renglón y la columna que sean escogidos para llevar a cabo la expansión de Laplace, y esta es una de las primeras cosas que se deben enseñar en un curso introductorio de Algebra Lineal.
La representación matricial G de un tensor métrico g se presta de modo natural para que incorporemos el concepto del determinante del tensor métrico, al cual para evitar que se le confunda con el tensor métrico g o con cualquier otra cantidad física se le simbolizará de color azul como g. Así, mediante la expansión de Laplace, podemos definir al determinante del tensor métrico de la siguiente manera:
PROBLEMA: Dado el siguiente tensor métrico:
expresar el determinante de dicho tensor evaluado en términos de los elementos del segundo renglón y sus cofactores correspondientes. Generalizar el resultado obtenido a un determinante de cualquier tamaño.
Cada cofactor de gij es el determinante que obtenemos al borrar el renglón i y la columna j en la que aparece gij, asociando el signo (-1) i + j a dicho determinante. Designando a los cofactores de g21, g22 y g23 como G(2,1), G(2,2) y G(2,3), respectivamente, tenemos entonces que dichos cofactores son:
Entonces, por la expansión de Laplace, tenemos que el determinante del tensor métrico será:
g = g21G(2,1) + g22G(2,2) + g23G(2,3)
La generalización hacia un determinante de cualquier tamaño empleando la convención de sumación para índices repetidos será:
g = gijG(i,j)
Tómese nota de que la convención de sumación se está aplicando aquí únicamente al índice j, no al índice i. Por esta razón y para evitar confusiones, es mejor escribir esta definición de determinante basada en la expansión por cofactores mostrando explícitamente el símbolo de la sumatoria que normalmente omitimos en otros casos:
Los cofactores no solo sirven para ayudarnos a encontrar el determinante g de una matriz. También nos sirven para encontrar la matriz inversa G-1 de una matriz G. Si se nos dá una matriz A y se nos pide obtener la matriz inversa de A, el procedimiento es el siguiente (nótese que en la matriz de cofactores Cij los componentes son colocados en forma transpuesta):
Esto significa que podemos obtener todos los componentes del tensor métrico conjugado g-1 = (gpq) a partir de los cofactores obtenidos de la matriz G del tensor métrico original g. La relación utilizada es la siguiente:
PROBLEMA: Obtener los componentes del tensor métrico conjugado g-1 que corresponden al tensor métrico g en coordenadas esféricas evaluando el determinante g y los cofactores necesarios a partir de la matriz G que corresponde al tensor métrico g.
Para el tensor métrico g expresado en coordenadas esféricas, puesto que la representación matricial G de los componentes de la métrica es:
el determinante g de su representación matricial será simplemente:
La evaluación de los componentes que corresponden al tensor métrico conjugado se muestran a continuación:
g11 = (cofactor de g11)/g = G(1,1) /g
g11 = 1
g22 = (cofactor de g22)/g = G(2,2) /g
g22 = 1/r²
g33 = (cofactor de g33)/g = G(3,3) /g
g33 = 1/r²
g21 = (cofactor de g12)/g = G(1,2) /g
g21 = 0
Podemos ver que para todos los demás gjk para los cuales g ≠ k, estos tendrán un valor de cero.
PROBLEMA: Demuéstrese que:
g11G(1,3) + g21G(2,3) + g31G(3,3) = 0
y una vez que esto ha sido demostrado, generalizar el resultado tanto para una expansión sobre renglones como para una expansión sobre columnas.
Apliquemos al siguiente determinante la expansión de Laplace para determinar a través de los cofactores el valor g del determinante llevando a cabo la expansión sobre la tercera columna sin fijarnos por el momento en la forma en la cual están escritos los elementos puestos en la tercera columna pero respetando al pie de la letra la notación que corresponde a cada cofactor asociado con dicha posición:
La expansión de Laplace del determinante llevada a cabo sobre los elementos de la tercera columna tal y como están escritos viene siendo la siguiente:
g = g11G(1,3) + g21G(2,3) + g31G(3,3)
Inspeccionando el determinante dado, nos damos cuenta de que tanto la primera columna del determinante como la tercera columna son iguales. Pero sabemos por las propiedades de los determinantes que si un determinante tiene dos renglones o dos columnas iguales, el valor del determinante será cero, lo cual ocurre en este determinante en el que la primera columna (de color magenta) es igual a la tercera columna (de color rojo). Esto implica que:
g = 0
lo cual a su vez implica que:
g11G(1,3) + g21G(2,3) + g31G(3,3) = 0
Podemos hacer una generalización de este resultado para una expansión llevada a cabo sobre una columna, la cual es la siguiente (llevando a cabo la sumación de términos sobre k):
g1jG(1,p) + g2jG(2,p) + g3 jG(3,p) + g4 jG(4,p) + ... = 0
Σk gkjG(k,p) = 0 si j ≠ p
Del mismo modo, la generalización para una expansión llevada a cabo sobre un renglón es la siguiente (llevando a cabo la sumación de términos sobre p):
gj1G(p,1) + gj2G(p,2) + gj3G(p,3) + gj4G(p,4) + ... = 0
Σk gjkG(p,k) = 0 si j ≠ p
PROBLEMA: Demostrar que bajo las relaciones dadas arriba para la obtención de los componentes del tensor métrico conjugado mediante el determinante g de la matriz de los componentes del tensor métrico y los cofactores de la misma, se cumple la siguiente relación:
gjk gpk = gpk gjk = δpj
Usando los resultados de los problemas anteriores, podemos afirmar que:
gjk G(j,k) = g
gjk [G(j,k)/g] = g/g
gjk gjk = 1
gjk [G(j,k)/g] = g/g
gjk gjk = 1
Y por otro lado:
gjkG(p,k) = 0 si j ≠ p
gjk[G(p,k)/g] = 0/g
gjk gpk = 0 para j ≠ p
gjk[G(p,k)/g] = 0/g
gjk gpk = 0 para j ≠ p
Los dos resultados se pueden resumir en uno solo con el delta de Kronecker:
Esta es la formalización matemática del hecho de que la contracción tensorial entre un tensor métrico g y su correspondiente tensor métrico conjugado g-1 nos resulta en el tensor delta Kronecker.
A continuación demostraremos una relación importante que será utilizada cuando tratemos el tema de la divergencia de un tensor.
PROBLEMA: Demostrar que:
Empezaremos con la definición de la expansión de Laplace para la evaluación del determinante g escogiéndose un renglón para llevar a cabo la sumatoria (si en vez de escoger un renglón escogemos una columna, esto en nada altera el resultado final):
A continuación tomaremos la derivada del determinante g con respecto a un elemento específico gjr de la matriz de la cual proviene el determinante. Esta operación la podemos llevar a cabo puesto que en su construcción el cofactor G(j,k) no contiene explícitamente al elemento gjk y por lo tanto podemos tratar al cofactor como si fuese una constante. En la sumatoria, la diferenciación no abarcará los términos para los cuales k ≠ r puesto que estos se volverán cero, quedándonos como el único elemento diferenciable aquél elemento para el cual k = r. A manera de ejemplo, se llevará a cabo la demostración de esto para una expansión de Laplace sobre el tercer renglón de una matriz 3x3:
Las derivadas posibles del determinante g son las siguientes:
Volviendo al cálculo simbólico, el resultado de la diferenciación será entonces:
Pero sabemos que:
Por otro lado, por la regla de la cadena tenemos lo siguiente:
Con lo cual llegamos a lo siguiente:
Anteriormente ya habíamos encontrado la siguiente relación entre símbolos de Christoffel de primer género (en la segunda línea se hace uso de la propiedad de simetría bajo la cual los símbolos de Christoffel permanecen iguales tras el intercambio de los dos primeros sub-índices):
Introduciendo esto en la relación de arriba y dejando que gjr actúe sobre cada símbolo de Christoffel de primer género convirtiéndolo en un símbolo de Christoffel de segundo género tras la elevación del tercer sub-índice se tiene entonces:
Puesto que queremos una expresión en la que haya un solo símbolo de Christoffel involucrado, y puesto que para nuestros fines podemos hacer que el símbolo de Christoffel Γjjm represente lo mismo que el símbolo de Christoffel Γrrm, podemos escribir j = r y tener así:
Despejando para Γrrm:
Esto lo podemos poner en una forma más compacta metiendo el símbolo g dentro de la derivada usando para ello la definición de la derivada del logaritmo natural:
Usando las propiedades de los logaritmos, el factor (½) puede entrar como una exponenciación fraccionaria de g, que viene siendo en realidad una raíz cuadrada. De este modo, llegamos a nuestro resultado final:
Obviamente, en la Teoría de la Relatividad, siendo una teoría basada en un 4-espacio, el determinante del tensor métrico será:
El tensor métrico más simple de todos es el que corresponde a un espacio-tiempo plano, Lorentziano, y ya sea que tomemos como elemento de línea (dándole a la velocidad de la luz un valor unitario) el siguiente:
ds² = - dt² + dx² + dy² + dz²
o que tomemos el siguiente:
ds² = dt² - dx² - dy² - dz²
el determinante del tensor métrico Lorentziano que identificaremos aquí como η y que corresponde a este elemento de línea será -1:
Es aquí en donde tiene su origen el signo negativo que encontramos en conversiones relativistas de coordenadas y en las fórmulas en las cuales aparece el determinante g del tensor métrico g dentro de una raíz cuadrada con signo negativo. Sin embargo, a la hora de llevar a cabo cálculos numéricos, en ningún momento tomamos la raíz cuadrada de algún número negativo venido de un determinante, y para evitar esta posibilidad (o más bien, confusión) en algunos textos se acostumbra encerrar a g entre las barras verticales que indican que se debe tomar el valor absoluto (siempre positivo) del mismo, apareciendo en dichas fórmulas como |g|. Los números imaginarios que provienen de la raíz cuadrada de números negativos no tienen cabida dentro de la Teoría de la Relatividad.