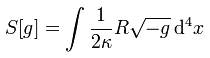El cálculo de variaciones aplicado a la física es usualmente justificado sobre la base de que la Naturaleza actúa de modo tal que ciertas cantidades importantes parecen ser minimizadas cuando tiene lugar un proceso físico. Esto lo tomamos como un postulado básico. De este modo, un rayo de luz reflejado de una superficie siempre recorre el camino más corto, de lo cual con la ayuda del cálculo infinitesimal se puede demostrar que el ángulo de reflexión debe ser igual al ángulo de incidencia. En 1657 Pierre de Fermat reformuló y amplió este principio postulando que un rayo luminoso siempre viaja de un punto a otro en un medio de modo tal que el camino recorrido es el que le toma la menor cantidad posible de tiempo, lo cual podemos tomar también como un postulado básico más amplio que el anterior. De este modo, Fermat pudo obtener no sólo la ley de reflexión sino también la ley de refracción descubierta experimentalmente por Willebrord Snell. La primera aplicación de un principio mínimo a la mecánica se remonta a 1747 cuando Pierre-Louise-Moreau de Maupertuis afirmó que el movimiento dinámico se lleva a cabo mediante un mínimo de acción o una acción mínima, término que subsiste hasta nuestros días sin cambio alguno. El principio de acción mínima de Maupertuis estaba basado no en argumentos matemáticos sino en argumentos teológicos, habiendo asentado que la acción es minimizada “a través de la sabiduría de Dios”. Fue hasta 1760 cuando dicho principio fue asentado sobre bases matemáticas firmes por Lagrange, utilizando para ello las principales variables físicas de un sistema (la posición y la velocidad) definiendo lo que vienen siendo los contenidos energéticos del sistema (la energía potencial y la energía cinética).
El basar los fundamentos que estamos buscando para la Teoría de la Relatividad en la Mecánica Lagrangiana tiene la enorme ventaja de que en la formulación de los principios básicos para obtener las ecuaciones del movimiento de un sistema no aparece explícitamente fuerza alguna. Esto es de importancia crucial para la Relatividad General porque dentro de la misma el concepto Newtoniano de la fuerza de atracción universal entre dos cuerpos ha sido eliminado por completo, y la única opción que nos queda es recurrir a eso que aún se sigue conservando invariante dentro de la Teoría de la Relatividad, la energía. Así, para derivar expresiones dentro de la dinámica relativista, la forma más “axiomática” de lograrlo es recurriendo a la mecánica Lagrangiana y al Principio de la Acción Mínima que en realidad no es más que una forma disfrazada de la aplicación del cálculo de variaciones a la física. Desde un principio, mucho antes que se formulara la Teoría Especial de la Relatividad, la Mecánica Lagrangiana recurriendo a las definiciones de la energía de un sistema (energía potencial, energía cinética, etc.) ya era superior a la mecánica Newtoniana basada en la definición de fuerzas y aceleraciones cuando lo que se trataba de lograr era la obtención de los sistemas de ecuaciones diferenciales que describen el comportamiento físico de un sistema. El mismo sistema de ecuaciones diferenciales que se obtienen para un sistema físico (por ejemplo tres masas pendulares conectadas con dos resortes) se puede obtener de una manera mucho más rápida recurriendo a la mecánica Lagrangiana que recurriendo a la mecánica Newtoniana ya que se prescinde por completo de la necesidad de tener que andar estimando las fuerzas que hay dentro del sistema.
Correspondió a Sir William Rowan Hamilton darle su definición final a los postulados de Lagrange formulando en dos papeles publicados en 1834 y 1835 lo que en la actualidad se conoce como el principio de Hamilton que puede ser enunciado de la manera siguiente:
“De todos los caminos posibles a lo largo de los cuales se puede mover un sistema físico de un punto a otro dentro de un intervalo especificado de tiempo, el camino que será recorrido es aquél que minimiza la integral de tiempo de la diferencia entre las energías cinética y potencial del sistema.”Es importante no perder de vista aquí el hecho de que al hablar de los caminos posibles no estamos hablando simplemente acerca de una distancia (medida en metros o centímetros) como la trayectoria seguida de un punto a otro sobre la superficie de una esfera. Estamos hablando de caminos en un sentido mucho más general, caminos en los que intervienen variables de velocidad o inclusive de aceleración que nos vienen produciendo las ecuaciones de movimiento de un sistema físico.
De este modo, cuando no basta la simple aplicación del cálculo infinitesimal para determinar un mínimo o un máximo que corresponderá a la solución de cierto problema físico de dinámica (como cuando se trata de obtener la ley de la reflexión de un haz luminoso o la ley de la refracción), es aquí cuando entra en el panorama el cálculo de variaciones mediante el cual una cantidad que se define como la integral de acción, o simplemente la acción, la cual es simplemente la integral del Lagrangiano L que clásicamente podemos identificar de inicio como la suma total de las expresiones de la energía cinética (K) de un sistema menos la suma total de las expresiones de la energía potencial del sistema (U), tomada dentro de cierto intervalo de tiempo:
∫ L dt
es sometida a una variación δ, proceso usualmente simbolizado de la siguiente manera:
δ ∫ L dt
y buscando la condición extrema en la cual obtengamos una solución estacionaria (principio de la acción mínima):
δ ∫ L dt = 0
debemos poder obtener, en principio, toda la información fundamental que nos permita describir el comportamiento del sistema.
De acuerdo con la definición dada arriba del principio de Hamilton, si tenemos a la mano el Lagrangiano para un sistema entonces la expresión variacional del principio de Hamilton usando coordenadas generalizadas qi es la siguiente:
en donde el punto arriba de la coordenada generalizada indica una derivada con respecto al tiempo (en cooordenadas Cartesianas, esto viene siendo simplemente la velocidad). Una vez que se ha logrado definir el Lagrangiano para un sistema físico, es un asunto directo encontrar con la ayuda del cálculo de variaciones las ecuaciones del movimiento que corresponden al sistema mediante las ecuaciones de Euler-Lagrange:
Compárese este sistema de ecuaciones con la ecuación de Euler obtenida en la entrada “La ruta geodésica” para calcular la ecuación de la distancia más corta entre dos puntos (geodésica) sobre una superficie:
Es así como las ecuaciones clásicas (diferenciales) del movimiento de un sistema pueden ser derivadas del principio de la acción mínima con la ayuda de las ecuaciones de Euler-Lagrange. Es así como toda la teoría del electromagnetismo de Maxwell puede ser derivada axiomáticamente a partir de la siguiente acción:
en donde la integral es en realidad una integral cuádruple llevándose a cabo la integración sobre cierto volumen de espacio tri-dimensional y el tiempo, y en donde F es el tensor electromagnético ó tensor de Faraday. Del mismo modo, uno de mayores esfuerzos requeridos para justificar los orígenes de la teorías modernas del campo cuántico se remiten a la búsqueda del Lagrangiano con el cual se pueda derivar tal o cual serie de fórmulas. Es así como la teoría de la Electrodinámica Cuántica (Quantum Electrodynamics o QED) tiene como punto de partida el siguiente Lagrangiano ó densidad Lagrangiana (la “densidad” Lagrangiana viene siendo a fin de cuentas lo mismo que un Lagrangiano ordinario, la única diferencia estriba en que el empleo casi fanfarrón de la palabra “densidad” denota que la integración para la evaluación de la acción se debe llevar a cabo sobre un espacio-tiempo cuatri-dimensional):
Y es así como la teoría de la Cromodinámica Cuántica (Quantum Chromodynamics o QCD) tiene como punto de partida la siguiente densidad Lagrangiana:
La acción proporciona inclusive el punto de partida para el desarrollo de la moderna teoría de las supercuerdas. Aunque no siempre es cosa fácil el lograr dar con el Lagrangiano que requerimos para fundamentar una nueva teoría sobre el cálculo variacional, hoy en día este paso es considerado como un paso indispensable para poder darle credibilidad y aceptación a toda nueva teoría.
PROBLEMA: Se deja caer un cuerpo desde una altura de 64 pies, y dos segundos después golpea contra el suelo. La distancia h recorrida por el cuerpo tras un tiempo t concebiblemente podría tomar cualquiera de las siguientes tres formas:
h = gt_____h = gt²/2_____h = gt3/4
siendo g la aceleración de la gravedad sobre la superficie de la tierra (igual a 32 pies/seg² en unidades del sistema inglés). Cualquiera de estas tres formas conduce a la misma respuesta de h = 64 pies para t = 2 segundos. Demostrar que la forma correcta es la que corresponde a la integral que dá un mínimo para la integral de acción de acuerdo con el principio de Hamilton.
Para resolver este problema, debemos calcular el valor de la integral I = ∫Ldt en cada uno de los tres casos, y determinar cuál de dichas integrales es la que produce el valor mínimo.
El Lagrangiano clásico L es igual a la energía cinética K menos la energía potencial U (puesto que al caer el cuerpo éste pierde energía potencial, el signo de la energía potencial será negativo al momento de introducir las expresiones cinéticas y potencial en el Lagrangiano):
L = K - U
L = (½) mV² + mgh = (½) m(dh/dt)² + mgh
Para el primer caso, h = gt, el Lagrangiano es:
L = (½) m(g)² + mg(gt)
L = (½) mg² + mg²t
L = (½) mg² + mg²t
La integral de acción correspondiente es:
Para el segundo caso, h = gt²/2, el Lagrangiano es:
L = (½) m(gt)² + mg(gt²/2)
L = mg²t²
L = mg²t²
La integral de acción correspondiente es:
Por último, para el tercer caso, h = gt3/4, el Lagrangiano es:
L = (½) m(3gt²/4)² + mg(gt3/4)
L = 9mg²t4/32 + mg²t3/4
L = 9mg²t4/32 + mg²t3/4
La integral de acción correspondiente es:
Podemos ver que de las tres integrales de acción la que tiene el valor mínimo es precisamente la que corresponde a la respuesta clásica de la distancia h recorrida por un cuerpo en un tiempo t cuando dicho cuerpo está en movimiento uniformemente acelerado, o sea la fórmula:
h = gt²/2
Esta misma fórmula se puede obtener de una manera más sencilla, sin recurrir al cálculo de variaciones, haciendo consideraciones elementales sobre un movimiento uniformemente acelerado a partir de la definición de la aceleración:
a = dv/dt
dv = adt
v = ∫a dt
dh/dt = ∫a dt
h = ∫ [ ∫a dt ] dt = ∫ [ ∫g dt ] dt = g ∫ [ ∫ dt ] dt
h = g ∫ [ t ] dt = g ∫ t dt
h = gt²/2
dv = adt
v = ∫a dt
dh/dt = ∫a dt
h = ∫ [ ∫a dt ] dt = ∫ [ ∫g dt ] dt = g ∫ [ ∫ dt ] dt
h = g ∫ [ t ] dt = g ∫ t dt
h = gt²/2
¿Entonces por qué razón habríamos de recurrir a algo más complejo y elaborado para obtener un resultado al que se puede llegar de una manera mucho más sencilla? Una respuesta que se puede dar aquí es que la forma “fácil” de obtener esta fórmula no está basada en un principio de acción mínima y por lo tanto no es derivable como parte de un programa axiomático. Otra razón que se puede dar es que, si bien en este caso ya se conoce de antemano la fórmula correcta de la cual esperamos que se produzca la integral de acción mínima, en otros casos no sólo no conocemos la fórmula sino que no hay más remedio que montar la integral y proceder a derivar la ecuación del movimiento a partir del principio de Hamilton (uno de tales problemas es el del braquistócrono que consiste en encontrar la ecuación de la curva a lo largo de la cual una esferita que se mueve a lo largo de dicha curva sin fricción bajo la influencia de la gravedad llegará de un punto a otro de la curva en el menor tiempo posible; y con la ayuda del cálculo de variaciones encontramos sin mayores problemas que la curva resulta ser una cicloide).
Aunque la Teoría Especial de la Relatividad cuando se dió a conocer al mundo por vez primera en 1905 fue fundamentada no sobre un principio variacional de acción mínima sino sobre dos postulados (el abandono del concepto del movimiento absoluto y la adopción de la velocidad de la luz como una constante universal que no depende del movimiento relativo de quien la mida), la Teoría Especial de la Relatividad puede ser derivada axiomáticamente del principio de la acción mínima usando para ello lo que se conoce como el Lagrangiano Relativista, lo cual veremos a continuación.
Puesto que en la axiomatización de una gran cantidad de áreas de la física, sobre todo las áreas nuevas, el Lagrangiano que se debe de utilizar como punto de partida es algo que se desconoce y la mayor parte del esfuerzo de los investigadores será consumido en tratar de “adivinar” la forma del Lagrangiano que se está buscando, en vez de empezar aquí de buenas a primeras con la postulación del Lagrangiano Relativista derivando resultados del mismo lo que haremos será analizar la manera en la cual podemos obtener el Lagrangiano Relativista, lo cual deberá servir como guía para la obtención de otros Lagrangianos que se desconocen al tratar problemas de naturaleza nueva.
Habiendo visto que el Principio de la Acción Mínima enuncia que para todo sistema mecánico debe de haber una cantidad llamada la acción S, y que la variación δS de dicha cantidad debe ser un mínimo para el comportamiento típico de un sistema, lo cual expresado en términos variacionales implica buscar el cumplimiento de la condición:
δS = 0
entonces para ser de utilidad en el fin que estamos buscando la acción S de un sistema relativista dentro del marco de la Teoría Especial de la Relatividad debe ser tal que esta sea una magnitud escalar que como tal permanezca invariante bajo transformaciones de Lorentz, y debe ser formulada como una integral que contenga como integrando un diferencial no mayor de primer orden. La única invariante que cumple con estos dos requisitos es el intervalo relativista espacio-tiempo ds entre dos eventos o un múltiplo escalar (multiplicado por una constante κ, letra griega kappa) de dicha integral. La acción S debe tener por lo tanto el siguiente aspecto:
S = κ∫ds
El intervalo relativista espacio-tiempo infinitesimal ds podemos expresarlo como:
ds = √ c²dt² - dx² - dy² - dz²
Sacando fuera cdt de la raíz cuadrada, y haciendo uso del hecho de que la magnitud instantánea de la velocidad v expresada en tres dimensiones en el espacio Cartesiano es:
tenemos entonces lo siguiente:
ds = (cdt) √1 - v²/c²
con lo cual:
S = cκ∫ √1 - v²/c² dt
La integral de acción puede ser expresada como una integral de tiempo del Lagrangiano L entre dos tiempos fijos t1 y t2:
S = ∫ Ldt
De aquí podemos leer el Lagrangiano relativista simplemente como:
L = cκ √1 - v²/c²
Para bajas velocidades, el Lagrangiano relativista L de un cuerpo moviéndose a una velocidad v debe reducirse al Lagrangiano clásico que no es más que la expresión para la energía cinética del cuerpo:
L = ½ mv²
Para comparar el Lagrangiano clásico L con el Lagrangiano relativista L, podemos llevar a cabo una expansión binomial del término bajo la raíz cuadrada mediante una serie de Taylor:
en donde o(v²) representa “los otros términos” residuales de la expansión binomial que pueden considerarse despreciables para los cálculos numéricos a bajas velocidades.
El primer término en esta expansión, cκ, es una constante, y por lo tanto no tendrá efecto alguno en las ecuaciones del movimiento. El segundo término, después de llevar a cabo la multiplicación y la simplificación, es:
(cκ) (- v²/2c²) = - kv²/2c
Comparando ambas L y L, la única manera en la cual el Lagrangiano relativista se pueda reducir al Lagrangiano clásico para bajas velocidades es haciendo κ = -m0c.
Se deduce, por lo tanto, que el Lagrangiano relativista dentro del marco de la Teoría Especial de la Relatividad debe ser:
L = - m0c²√1 - v²/c²
Cuando hay una energía potencial U de por medio además de la energía relativista identificada por el Lagrangiano, entonces acorde con la definición clásica del Lagrangiano la definición que acabamos de obtener se modifica de la manera siguiente:
L = - m0c²√1 - v²/c² - U
Obsérvese cuidadosamente que este Lagrangiano no está dado por L = K - U, puesto que la expresión relativista para la energía cinética K está dada por:
K = γm0c² - m0c²
Una vez que se tiene la expresión del Lagrangiano de algo, se puede obtener del mismo la expresión correspondiente de la cantidad de movimiento mediante la relación que interconecta al momentum canónico (formal) con el Lagrangiano:
pi = ∂L / ∂vi
Tomando la derivada parcial del Lagrangiano relativista L con respecto a la velocidad v, obtenemos para la cantidad de movimiento:
p = ½ (2m0v√1 - v²/c²)
p = m0v√1 - v²/c²
p = γm0v
p = m0v√1 - v²/c²
p = γm0v
Esta es precisamente la misma expresión para el momentum relativista obtenida con mayores dificultades (sin la comodidad del método de Lagrange) en una entrada anterior.
PROBLEMA: Dado el siguiente Lagrangiano para un oscilador harmónico simple relativista:
L = m0c² (1 - √1 - β²) - (½) kx²
en donde β = V/c, (1) encontrar la ecuación del movimiento que corresponde a dicho Lagrangiano, y (2) demostrar tras esto que la expresión puede ser integrada para dar como energía del sistema:
E = m0c² + (½) ka²
en donde a es la excursión máxima de la partícula oscilante desde el punto de equilibrio.
Del Lagrangiano relativista, para poder recurrir a la ecuación de Euler-Lagrange llevamos a cabo primero los siguientes cálculos:
Entonces con q = x, la aplicación de la ecuación de Euler-Lagrange (en este caso n = 1 y sólo tenemos una ecuación) nos produce lo siguiente:
Tomando la derivada con respecto al tiempo del primer término, obtenemos finalmente la ecuación del movimiento del oscilador harmónico simple relativista (usamos el punto encima para denotar derivación con respecto al tiempo de la variable):
Regresamos a la penúltima ecuación para llevar a cabo la integración de la misma, para lo cual la reescribimos el primer término del modo siguiente:
Pero dx/dt es simplemente la velocidad V que podemos modificar como:
dx/dt = V = c (V/c) = cβ
Entonces el primer término se nos convierte en:
Recurrimos ahora a la relación del diferencial del producto de dos variables:
d(uv) = udv + vdu
udv = d(uv) - vdu
udv = d(uv) - vdu
y haciendo la diferenciación de esto con respecto a x:
junto con la siguiente identificación de variables:
tenemos entoncoes la siguiente expansión que será utilizada para facilitar la integración :
La segunda cantidad dentro del paréntesis a su vez puede ser reescrita dejando todo como sigue:
Con esto último la integración que queremos llevar a cabo se convierte en un asunto trivial con lo cual lo que vamos a integrar:
se nos converte ya integrado en lo siguiente:
siendo E la constante de integración. Podemos simplificar los dos primeros términos en uno solo llegando a:
E = m0c²/√1 - β² + (½) ka²
La constante de integración E puede ser evaluada en el punto de amplitud máxima x = a, cuando el resorte oscilante está totalmente estirado con una velocidad V = 0 lo cual a su vez dá β = 0. Llevando a cabo esto, obtenemos la expresión para la energía del sistema que es simplemente:
E = m0c² + (½) ka²
De este modo, la energía del oscilador harmónico simple relativista es igual a la energía potencial del resorte en su amplitud máxima sumada a la energía en reposo m0c² de la masa oscilante, algo que quizá podíamos haber anticipado intuitivamente.
Quienes hayan tomado un curso de mecánica a nivel de licenciatura sabrán que además de la formulación de la Mecánica Lagrangiana, basada en la definición del Lagrangiano, existe otra formulación clásica de la mecánica, la Mecánica Hamiltoniana, basada en la definición del Hamiltoniano. Y la pregunta que se harán es: ¿podemos hablar de un Hamiltoniano relativista? La respuesta es afirmativa, y en este caso todo lo que tenemos que hacer es tomar la definición del Hamiltoniano clásico (para una partícula):
H = pv - L
y en la misma meter reemplazar el Lagrangiano “clásico” con un Lagrangiano relativista como los que hemos manejado arriba, reemplazando también el momentum “clásico” p = mv con el momentum relativista p = γm0v.
PROBLEMA: Obtener el Hamiltoniano relativista para una partícula.
El Hamiltoniano relativista estará dado por:
H = pv - L = (γm0v) v - L
H = γm0v² - L
Metemos aquí la expresión obtenida arriba para el Lagrangiano relativista:
H = γm0v² + m0c²√1 - v²/c² + U
H = m0v²/√1 - v²/c² + m0c²√1 - v²/c² + U
H = m0v²/√1 - v²/c² + m0c²√1 - v²/c² + U
La simplificación inmediata de los dos primeros términos nos produce la siguiente expresión:
H = m0c²/√1 - v²/c² + U
La cantidad en el primer término la identificamos de inmediato con la energía total E de la partícula (véase la entrada “La ecuación más famosa de Einstein”) cuando no se ha incluído energía potencial alguna bajo consideración:
E = γm0c²
Entonces:
H = E + U
De este modo, el Hamiltoniano relativista resulta ser igual a la energía total total del sistema, incluídas la energía cinética, la energía en reposo, y la energía potencial.
Hemos visto cómo se puede fundamentar a la Teoría Especial de la Relatividad sobre el cálculo de variaciones, y cómo para poder avanzar necesitamos primero definir un Lagrangiano para el sistema que está bajo estudio, con lo cual podemos obtener la ecuación del movimiento del sistema. La formulación de la Teoría Especial de la Relatividad sobre principios variacionales partiendo del principio de la acción mínima nos lleva naturalmente a considerar la posibilidad de que se pueda hacer lo mismo para poder derivar matemáticamente del cálculo de variaciones las ecuaciones de campo de la Relatividad General. Esto es algo que desde un principio ocupó la atención de Einstein que estaba interesado en darle una justificación a sus ecuaciones de campo mostrándolas como algo susceptible de ser obtenido de principios más fundamentales. El recurso del Lagrangiano relativista que se ha postulado arriba a partir del principio de la acción mínima recurriendo al cálculo variacional es algo de lo cual se pueden derivar conceptos fundamentales en la Teoría Especial de la Relatividad tales como la definición del momentum relativista. Y resulta que la metodología usada arriba también puede ser aplicada a la Relatividad General, aunque las suposiciones iniciales requeridas para lograr obtener el resultado final no sean tan sólidas y convincentes desde el punto de vista filosófico como pudiera esperarse, siendo una de las inconveniencias el hecho de que la acción Einstein-Hilbert propuesta por Einstein en competencia intelectual con David Hilbert es indefinida en el caso de una hoja (manifold) no-compacta, e inclusive esta acción se vuelve infinita aún en el caso de un espacio-tiempo plano. De cualquier manera, a través de la acción Einstein-Hilbert ambos demostraron la posibilidad de poder derivar las ecuaciones de campo de la Relatividad General a partir de una integral de acción. La derivación de las ecuaciones de la Relatividad General mediante una acción tiene varias ventajas, siendo la principal que nos permite una unificación relativamente sencilla con otras teorías clásicas de campos (tales como la teoría del electromagnetismo de Maxwell) que también puedan ser formuladas sobre el principio de una acción. La acción tiene una ventaja adicional, ya que permite la fácil identificación de cantidades físicas conservadas en el curso de un proceso físico gracias a un conocido teorema, el teorema de Noether, para lo cual solo se requiere identificar las simetrías que existan en la acción de un sistema.
Para la Relatividad General, la acción utilizando a una cantidad g como variable resulta ser (obsérvese que la integración de la acción se lleva a cabo aquí en un 4-volumen):
en donde:
es el determinante de la metrica del espacio-tiempo plano (Lorentziano), R es el escalar de Ricci, y κ es una constante universal:
κ = 8πG/c4
Como puede verse, el Lagrangiano (o mejor dicho, la densidad Lagrangiana) aquí es:
Para tomar en cuenta la presencia de masa-energía (o mejor dicho, campos de materia-energía) es común añadir al Lagrangiano de la Relatividad General un término adicional L, teniendo con esto la siguiente accion para la Relatividad General:
Con esto tenemos todo lo que necesitamos para poder derivar, a partir de esta última accion, las ecuaciones de campo de la Relatividad General. Esto, filosóficamente hablando, asienta a la Relatividad General sobre principios variacionales, y le dá una justificación más formal a la teoría haciéndola más axiomática y menos intuitiva.
Aunque la fundamentación de la Relatividad General, si es que ha de fundamentarse sobre algo a partir de lo cual sus primeros principios puedan ser derivados, tiene como punto de partida predilecto el principio de la acción mediante un Lagrangiano adecuado, también es posible intentar llevar a cabo una formulación de la misma mediante un Hamitoniano con el cual sea posible escribir las ecuaciones del movimiento de la Relatividad General en la forma típica de las ecuaciones de Hamilton. Tal metodología fue desarrollada por Richard Arnowitt, Stanley Deser y Charles Misner, hoy conocida con el nombre formalismo ADM. Sin embargo, y a fin de cuentas, la formulación ADM termina basándose en el siguiente Lagrangiano:
Justo cuando todo parece haberse dicho sobre la fundamentación formalizada de la Relatividad General sobre principios variacionales, debemos contender ahora con otra ruta alterna que nos permite derivar las mismas ecuaciones de campo no sobre principios variacionales, sino ¡a partir de la termodinámica!
Al estudiar el tema de la relación que hay entre los agujeros negros y la entropía a través de la segunda ley generalizada de la termodinámica propuesta por Jacob Bekenstein partiendo a su vez de la similitud que hay entre el teorema del área para los agujeros negros y la segunda ley de la termodinámica en su enunciación clásica (estadística) sumado al descubrimiento teórico hecho por Hawking de que los agujeros negros se comportan como radiadores térmicos emitiendo partículas constantemente, ya se habían mencionado las enormes dudas y sospechas de que detrás de todas estas similitudes haya no meras coincidencias sino un mar de fondo que se nos está escapando y que no alcanzamos a ver en estos momentos.
La posibilidad de la derivación de las ecuaciones de campo de la Relatividad General a partir de argumentaciones basadas en la termodinámica fue demostrada en 1995 por Theodore (Ted) Jacobson, quien probó es posible que las ecuaciones de campo de Einstein puedan ser derivadas como una ecuación de estado a partir de argumentos termodinámicos. Para lograr su demostración, Jacobson utilizó la ecuación de Raychaudhuri y la relación de proporcionalidad que hay entre el área A y la entropía S para todos los horizontes locales de aceleración (y al decir horizontes locales de aceleración no estamos haciendo referencia específica y exclusiva al horizonte de evento de un agujero negro, estamos hablando del entorno de un observador que se está acelerando en el espacio-tiempo con una rapidez extraordinaria siendo por lo tanto capaz de percibir la radiación predicha por el efecto Unruh). La ecuación de Raychaudhuri es considerada como un resultado fundamental que describe el movimiento de pedacitos de materia cercanos el uno al otro, y es considerada un lema matemático importante requerido para poder llevar a cabo la demostración de los teoremas de singularidad Penrose-Hawking así como para el estudio de soluciones exactas a las ecuaciones de campo de la Relatividad General, aunque también es de interés por cuenta propia ya que ofrece una validación general y sencilla de nuestra creencia intuitiva de que la gravedad debe manifestarse dentro de la Relatividad General como una fuerza de atracción entre dos pedacitos de masa-energía del mismo modo que ocurre dentro del esquema Newtoniano. La ecuación de Raychaudhuri suele aparecer escrita en los textos en la siguiente forma (los puntos sobre las variables indican una derivada con respecto al tiempo propio; obsérvese que en el último término estamos tomando la derivada covariante del tensor mixto X llevando a cabo tras esto una operación de contracción con la igualación de los índices que activa a la convención de sumación culminándolo con la toma de la derivada convencional con respecto al tiempo propio):
en donde
σ² = σmn σmn
ω² = ωmn ωmn
ω² = ωmn ωmn
son invariantes cuadráticos (positivos) del tensor de esfuerzo cortante (en inglés, shear) σab:
y ωab es el tensor de vorticidad:
en donde:
es el tensor de expansión, θ es la traza del tensor conocida como el escalar de expansión, y:
hab = gab -XaXb
es el tensor de proyección hacia los planos ortogonales a X. Finalmente, tenemos la traza del tensor de marea o tensor electrogravítico (conocido también como el escalar de Raychaudhuri) definido como (obsérvense en ambos lados de esta ecuación tensorial los índices repetidos que activan la convención de sumación):
En la esencia de la demostración dada por Jacobson, se utiliza como punto de partida una fórmula termodinámica fundamental conocida como la ecuación de Clausius que nos relaciona la transferencia de un cantidad infinitesimal de energía (o mejor dicho, masa-energía) dQ a cierta temperatura T con el correspondiente aumento infinitesimal en entropía dS que se produce a causa de dicha transferencia:
dS = dQ/T
y la cual tiene que ser reinterpretada definiendo a dS como el cambio ocurrido a través de un cuarto del área del horizonte local de aceleración (en unidades de Planck), definiendo a dQ como el flujo de energía a través de ese horizonte local de aceleración, y definiendo a T como la temperatura Unruh medida por un observador acelerándose dentro del horizonte local de aceleración (la temperatura Unruh producida por el efecto del mismo nombre es tratada al final de la entrada “Los agujeros negros IV: Evaporación”). Jacobson demostró que el requerimiento esencial para que las ecuaciones de campo de la Relatividad General puedan ser derivadas a partir de la ecuación (redefinida) de Clausius es que dicha ecuación tiene que ser válida para todos los horizontes locales de aceleración a través de cada punto en el espacio-tiempo.
La demostración obtenida por Jacobson de que las ecuaciones de campo de Einstein pueden ser derivables termodinámicamente como una ecuación de estado implica como consecuencia la existencia de algunos grados de libertad cuánticos fundamentales de donde debe ser posible obtener las ecuaciones de campo mediante una manipulación adecuada de la función de partición correspondiente, una conexión que hasta la fecha no se ha podido lograr.
Tiempo después del descubrimiento hecho por Jacobson, en el 2006 se publicó en el Physical Review Letters un documento breve titulado “Non-equilibrium Thermodynamics of Spacetime” (disponible gratuitamente en arXiv) en donde Jacobson junto con los investigadores Christoper Eling, Christoper y Raf Guedens cubren la termodinámica del espacio-tiempo en situaciones fuera del equilibrio termodinámico, mostrando con ello la forma en la cual se ha ido avanzando en la fusión entre la Relatividad General y la termodinámica. Una propuesta todavía más interesante es la que fue publicada también en arXiv el 4 marzo de 2009 bajo el título “The Einstein equations for generalized theories of gravity and the thermodynamic relation dQ = T dS are equivalent”, con la cual sus autores Ram Brustein y Merav Hadad intentan demostrar que las ecuaciones del movimiento de la Relatividad General son equivalentes a la relación de Clausius dQ = T dS, utilizando para ello una definición más extendida de la entropía de carga de Noether, agregando haber encontrado que esta entropía de carga de Noether obedece también la segunda ley de la termodinámica si el tensor energía-momentum obedece una condición de energía nula. El corolario de este trabajo, según afirman sus autores, es que la gravedad que vemos manifestada a una escala macroscópica no es más que una manifestación de la termodinámica del vacío, con lo cual consideran concluída la propuesta de Jacobson de que las ecuaciones de campo de la Relatividad General pueden ser expresadas como una ecuación termodinámica de estado. Obviamente, para que este trabajo sea válido se requiere que el fenómeno mecánico-cuántico de creación de partículas virtuales en el vacío a causa de las fluctuaciones del vacío sea también un hecho incontestable.
Si bien las ecuaciones de campo de la Relatividad General pueden ser derivadas a partir de la termodinámica, no es posible derivar la termodinámica a partir de la Relatividad General. ¿Significa esto que la Termodinámica deba ser considerada como algo más fundamental que la Relatividad General? Esto es material de reflexión filosófica que nos demuestra que aún nos queda un buen trecho por recorrer antes de que podamos proclamar que se ha agotado todo lo que la física nos permite descubrir.
La Relatividad General no sólo puede ser derivada a partir de principios termodinámicos. Los investigadores de la teoría de las supercuerdas han estado trabajando afanosamente para demostrar la factibilidad de que se pueda formular una “Teoría del Todo” que lo explique precisamente todo, a partir, claro está, de la teoría que ellos mismos han estado desarrollando y que suponen que es la tan ansiada y elusiva “Teoría del Todo” que se le escapó de las manos al mismo Einstein. Y hay todavía otras rutas de interés. Aquí se mencionará una de ellas propuesta por Christoph Schiller en su trabajo titulado “General Relativity and Cosmology Derived From Principle of Maximum Power or Force” publicado en el International Journal of Theoretical Physics en septiembre de 2005, de acuerdo con el cual se demuestra que las ecuaciones de campo de la Relatividad General se pueden derivar poniendo un límite a la fuerza F o a la potencia P que se pueden dar en la Naturaleza, teniendo dichos límites los valores de c4/4G y c5/4G. Específicamente, Schiller propone los siguientes valores para una fuerza máxima F y una potencia máxima P que puedan ocurrir en la Naturaleza que están dadas por las siguientes relaciones:
señalando que cualquiera de estas dos relaciones puede ser tomada como el postulado básico. La prueba a la que recurre Schiller utiliza un resultado previo obtenido por Theodore Jacobson, y argumenta que todos los datos experimentales son consistentes con los límites propuestos por él. Aplicando los límites propuestos por él, estos predicen la obscuridad de la noche del Universo (resolviendo con ello la famosa paradoja de Olbers según la cual el cielo nocturno se debería de ver iluminado y no oscuro dada la cantidad de estrellas en el firmamento así como las distancias de las mismas hacia la Tierra) y el factor observado de escala, proponiendo otras pruebas experimentales para la verificación de su hipótesis. En su trabajo examina los principales contra-argumentos y paradojas tales como las transformaciones bajo empujes, la fuerza que se debe sentir en el horizonte de evento de un agujero negro y el “problema de la montaña” así como el contraste de su teoría contra otras teorías escalar-tensor de la gravitación, indicando que la resolución de las paradojas clarifica el por qué la máxima fuerza y la máxima potencia permanecieron ocultas por tanto tiempo. Argumenta también que la derivación de las ecuaciones de campo de la Relatividad General como él lo propone desempeñan el mismo papel en la Relatividad General como la máxima velocidad lo hace en la Teoría Especial de la Relatividad. Este trabajo de Christoph Schiller se puede obtener del siguiente enlace:
http://www.springerlink.com/content/p68p73jru7084772/
Sobre el trabajo inicial emprendido para asentar la Relatividad General sobre principios variacionales llevado a cabo por Einstein conjuntamente (o mejor dicho, independientemente, en sana competencia para reclamar los méritos del logro) con el matemático David Hilbert mediante una acción conocida como la acción Einstein-Hilbert, la cual es una expresión matemática que representa una generalización hacia el espacio-tiempo cuatri-dimensional del principio clásico de la acción mínima, y la cual al ser extremizada produce las ecuaciones de campo de Einstein, se puede obtener más información sobre este tema en los siguientes enlaces:
http://en.wikipedia.org/wiki/Einstein%E2%80%93Hilbert_action
http://www.physics.thetangentbundle.net/wiki
/General_relativity/Einstein-Hilbert_action
Otra fuente de consulta útil es el libro “The Mathematical Theory of Relativity” del Professor Arthur Stanley Eddington, uno de los pioneros en el campo de la Relatividad General, el cual dá un tratamiento completo sobre la acción Einstein-Hilbert a partir de la sección 60 del libro titulada precisamente “Acción”, la cual empieza con una acción cuatri-dimensional basada en la acción clásica y en donde se demuestra cómo dicha acción es convertida a una integral sobre un escalar G.
Además de la acción Einstein-Hilbert, en la literatura podemos encontrar mención a otro tipo de variación conocida como la variación de Palatini, de la cual podemos encontrar mayores referencias en el siguiente enlace:
http://en.wikipedia.org/wiki/Palatini_variation