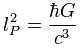Para fines de simplificacion de calculos en los trabajos cientificos relacionados con la fisica y la quimica, Planck propuso un nuevo sistema de unidades basado no en el sistema convencional del metro-kilogramo-segundo (MKS) o del centímetro-gramo-segundo (CGS) del sistema internacional SI de unidades, sino en un nuevo sistema de unidades basado las tres principales constantes físicas, creando así lo que llamó un sistema de unidades naturales (por estar basado en constantes físicas de la naturaleza y no en estándares arbitrarios sin base física como el metro, el kilogramo y el segundo). Planck argumentó que este sistema de unidades naturales permanecería igual siempre y cuando la ley de la gravedad (dependiente de la constante de gravitación universal G), la velocidad de la luz en el vacío c, y los principios de la termodinámica, permanecieran invariables. Las unidades naturales de Planck suelen ser llamadas (en broma) entre los físicos como “las unidades de Dios” porque al depender de constantes físicas su uso elimina las arbitrariedades antropocéntricas en el sistema de unidades.
Planck enlistó su sistema de unidades “naturales” dándoles valores curiosamente cercanos a los que utilizamos hoy en la actualidad, en un trabajo presentado en mayo de 1899 a la Academia Prusiana de Ciencias bajo el título “Über irreversible Strahlungsvorgänge” aparecido en el volumen 5 de la publicación periódica Sitzungsberichte der Preußischen Akademie der Wissenschaften. Es importante señalar que al momento de presentar Planck su propuesta la Mecánica Cuántica aún no se había inventado, y el mismo aún no había descubierto, la teoría de la radiación térmica del cuerpo negro (esta sería publicada hasta diciembre de 1900) en donde la constante h hizo su aparición por vez primera y por la cual Planck fue galardonado con el premio Nobel. Tampoco había hecho su aparición la Teoría General de la Relatividad, ni siquiera la Teoría Especial de la Relatividad, y mucho menos se sabía de lo que pudiera ser un agujero negro.
La parte relevante del trabajo (en lo que concierne a las unidades naturales propuestas por Planck) presentado por Planck en 1899 nos dejan alguna confusión sobre cómo pudo concebir sus unidades de longitud, masa, tiempo, temperatura, etc., que el día de hoy definimos utilizando la constante h-barra (la constante de Planck dividida entre 2π conocida también como la constante reducida de Planck) y que son motivadas hoy recurriendo a referencias en la Física Cuántica, en una época en la que no se conocían ni la constante h-barra ni la Física Cuántica. Es interesante notar también que en su trabajo Planck hace referencia a la posibilidad de civilizaciones extraterrestres al asentar en el mismo lo siguiente acerca de sus unidades naturales:
- “Bedeutung für alle Zeiten und für alle, auch ausserirdische und ausser menschliche Culturen nothwendig behalten und welche daher als ‘natürliche Maasseinheiten’ bezeichnet werden können.”
- “...Estas necesariamente retienen su significado para todos los tiempos y para todas las civilizaciones, inclusive extraterrestres y no-humanoides, y por lo tanto pueden ser designadas como ‘unidades naturales’...”
En lugar de seguir la línea de argumentación original dada por Planck para justificar su sistema de unidades naturales (cargado de razonamientos que muestran su dominio del electromagnetismo y la termodinámica), seguiremos aquí un enfoque más moderno que ciertamente nos resultará más claro.
Para que la gravedad pueda estar acoplada con la materia se requiere una constante de acoplamiento G, la constante de gravitación universal, la cual tiene unidades de longitud sobre masa. Al considerar la atracción gravitatoria entre dos cuerpos, si uno permite que la Mecánica Cuántica entre en el panorama uno eventualmente se topará con lo que llamamos escala de Planck. Para ello, considérese primero una partícula cuántica que posee cierta masa en reposo m0 y que posee otra propiedad física que llamamos la longitud de onda Compton λ, estando dada la relación entre ambas por la constante de Planck h:
PROBLEMA: Hallar la longitud de onda Compton para un electrón (cuya masa en reposo es 0.511 Mev).
Teniendo la masa en reposo como dato dado, para fines de cálculo resulta conveniente reescribir la relación de la longitud de onda Compton de la manera siguiente:
La cantidad hc que aparece en el numerador es una cantidad tan utilizada que vale la pena asignarle de antemano su valor numérico:
hc = (4.136·10-15 eV·segundo)(3·108 metros/segundo)
hc = 1.24·10-6 eV·metro
hc = 1.24·104 eV·Å
hc = 1.24·10-6 eV·metro
hc = 1.24·104 eV·Å
Para el electrón su longitud de onda Compton será:
λ = hc/m0c² = (1.24·104 eV·Å)/(0.511 MeV)
λ = 0.0243 Å
λ = 0.0243 Å
PROBLEMA: Hallar la longitud de onda Compton para un protón (cuya masa en reposo es 938.3 Mev).
Procedemos de manera idéntica a como lo hicimos en el problema anterior:
λ = hc/m0c² = (1.24·104 eV·Å)/(938.3 MeV)
λ = 1.32·10-5 Å
λ = 1.32·10-5 Å
Dando por hecho que cada partícula atómica sea capaz de ejercer una atracción gravitacional sobre otra, debemos contender con el hecho de que nuestros conocimientos actuales del mundo sub-atómico nos indican que es imposible fijar con absoluta certeza a cualquier partícula atómica si se considera a dicha partícula como formada por un paquete de onda. Esto es lo que nos dice la Mecánica Cuántica Ondulatoria, a esto es a lo que nos lleva el aspecto ondulatorio de la materia confirmado por numerosos experimentos. Podemos medir la probabilidad de que la partícula atómica se encuentre dentro de cierta región, pero su localización exacta nos será incierta, y esa probabilidad podrá tener una distribución estadística Gaussiana para una sola partícula. Supondremos que la mayor parte de la onda está confinada precisamente dentro de lo que viene siendo la longitud de onda Compton de la partícula.
A continuación considérese que una partícula pueda ser localizada en el espacio tanto como sea posible tomando en cuenta su naturaleza ondulatoria, quedando definido su “alcance” por su longitud de onda Compton (para el paquete de onda mostrado, podemos suponer que la partícula está localizada entre -5 y +5 unidades en el diagrama, con lo cual su longitud de onda Compton sería igual a 10 unidades, siendo esta una onda que se propaga de izquierda a derecha):
En otras palabras, estamos considerando a una partícula con masa m0 localizada dentro de cierta región del espacio-tiempo con una “longitud de alcance” dada por la longitud de onda Compton de la partícula. Podemos ver de la fórmula que entre mayor sea la masa en reposo m0 de la partícula, tanto menor será su longitud de onda λ. La longitud de onda Compton (y por ende la incertidumbre de la posición que ocupa una partícula en el espacio-tiempo) se va haciendo más y más pequeña conforme va aumentando la cantidad de masa.
Teniendo lo anterior en mente, si tenemos a dos electrones situados a cierta distancia el uno del otro, los podemos representar como dos
 “paquetes de onda” que ejercen entre sí una atracción gravitacional:
“paquetes de onda” que ejercen entre sí una atracción gravitacional:Hasta aquí podemos reconciliar a la Relatividad General con la naturaleza cuántica de la materia, mientras los electrones no estén “lo suficientemente juntos”. El problema se nos viene encima cuando intentamos juntar a las dos “ondas de materia” dentro de su longitud de onda Compton de modo tal que las regiones de probabilidad que representan la posicion de cada partícula se van traslapando una con otra:
porque en este caso, ¿qué exactamente es lo que está ejerciendo una atracción gravitacional sobre qué? ¿Se trata acaso de una probabilidad ejerciendo una atracción sobre otra? ¿Y qué gravedad puede haber entre dos partículas cuando ambas están completamente traslapadas? ¿Pierden acaso su identidad? Esta situación hipotética de tratar de juntar dos electrones dentro de una región de extensión igual a la de su longitud de Compton se antoja inverosímil porque para poder lograr tal cosa ambos tendría que ocupar, considerados como partículas puntuales, el mismo lugar en el espacio. La única forma de “casi” lograrlo sería revocando la hipótesis de que cada electrón se extiende hasta una distancia igual a su longitud de Compton, suponiendo ahora que cada electrón puede ser confinado a distancias mucho menores que su longitud de Compton. Sin embargo, esto tiene un límite. Sabemos de la Relatividad General que si empujamos a cualquier cantidad fija de materia hacia una región más y más pequeña, eventualmente esta se convertirá en un agujero negro, para lo cual debemos tomar en cuenta el radio de Schwarzschild para el horizonte de evento de un agujero negro que es rs = 2GM/c².
En el ejemplo mostrado, afortunadamente entra en acción la fuerza repulsiva eléctrica entre los dos electrones sobreponiéndose por vasto margen a la influencia gravitacional que pueda ejercer el uno sobre el otro. Pero tratándose de dos partículas como lo son los neutrones, sin carga eléctrica que los haga repelerse mutuamente, la interrogante se nos viene nuevamente encima.
Aunque alguna vez se propuso la posibilidad de que las partículas sub-atómicas como el electrón, siendo singularidades en la métrica del espacio tiempo g, pudiesen ser agujeros negros, unos cálculos elementales descartan tal posibilidad. De acuerdo con la métrica de Schwarzschild, para el Sol obtenemos un radio de Schwarzschild rs = 2GM/c² de aproximadamente unos 3 kilómetros, bastante al interior del Sol, razón por la cual al Sol no se le considera un agujero negro ya que para ser un agujero negro tendría que tener toda su masa situada dentro de este radio. Para el Sol, su tamaño mecánico-cuántico, su longitud de onda Compton, es esencialmente cero (no hay mucha incertidumbre sobre la posición en la cual el sol está localizado dentro del sistema solar), pero para el electrón ya vimos arriba que su longitud de onda Compton es de λ ≈ 2.43·10−12 metros. Por otro lado, poniendo números, para un electrón su radio de Schwarzschild rs resulta ser igual a 1.35·10−51 metros, una distancia ciertamente mucho menor que su longitud de onda Compton de 2.43·10−12 metros. Aunque para un electrón su longitud de onda Compton es una distancia muy pequeña, ciertamente es mucho mayor que su radio de Schwarzschild, de modo tal que desde la perspectiva de la Mecánica Cuántica la mayor parte del electrón está situada fuera de su horizonte de evento. Esta es la razón del por qué a las partículas sub-atómicas, aunque se les considere singularidades en el entramado de espacio-tiempo del Universo, no se les considera que sean agujeros negros.
De los límites que tenemos para el posible “tamaño” del electrón, por el lado máximo 2.43·10−12 metros y por el lado mínimo 1.35·10−51 metros, es natural que despierte en nosotros la sospecha de que pueda haber un tamaño “intermedio” entre estos dos valores, no solo para el electrón sino para cualquier otra partícula, en el cual la Relatividad General y la Mecánica Cuántica se confronten cara a cara. Puesto que el límite máximo representa una condición de la Mecánica Cuántica y el límite mínimo representa una condición de la Relatividad General, esto supondría que la Relatividad General sigue siendo válida a escalas de distancia mucho menores que las distancias en las cuales la Mecánica Cuántica ya está firmemente en control, lo cual no es creíble. La búsqueda de una longitud intermedia en la cual la Relatividad General empieza a verse en aprietos al mostrar la Mecánica Cuántica sus efectos nos lleva a la búsqueda de una longitud crítica que posiblemente pueda ser derivada a partir de constantes físicas fundamentales, tales como la constante de la gravitación universal representando a la Relatividad General, y la constante de Planck representando a la Mecánica Cuántica. Y resulta que las unidades naturales propuestas por Planck, aunque creadas no quizá con esta intención en mente, son precisamente las que cumplen con este objetivo. Para poder seguir adelante, necesitamos fijarnos un criterio que nos sirva de guía. Tal vez el criterio más obvio sea aquél bajo el cual queremos determinar una masa crítica que corresponda a la longitud crítica que estamos buscando, definiéndola como aquella masa para la cual su radio de de Schwarzschild sea del mismo tamaño que su longitud de onda Compton. Este criterio ciertamente pone cara a cara a la Relatividad General con la Mecánica Cuántica. Usando este criterio como guía, podemos definir lo que hoy se conoce como la masa de Planck dada por la fórmula:
y cuyos valores calculados, tanto en unidades de masa convencionales en el sistema de unidades MKS como en su equivalente energético de acuerdo con la relación E = mc² para masa-energía, usando las mediciones que hoy se tienen para las constantes físicas, resultan ser (en la página 480 de su trabajo, Planck obtiene 5.56·10-5 gramos):
mp = 2.17644·10-8 Kilogramos
mp = 1.220862·1019GeV/c²
mp = 1.220862·1019GeV/c²
Es importante notar que Planck lo que buscaba era definir una longitud universal a partir de constantes físicas universales, mientras que lo que nosotros buscamos es definir una masa tal que esta masa sea la masa que una partícula debe tener para que su radio de Schwarzschild sea del mismo tamaño que su longitud de onda Compton. Y resulta que ambos criterios conducen a la misma conclusión para el mismo orden de magnitud.
PROBLEMA: Usando la aproximación de la fórmula para el radio de Schwarzschild (prescindiendo de la constante numérica 2) y la longitud de onda Compton, obtener la fórmula para la masa de Planck.
La extensión del radio de Schwarzschild es aproximadamente (prescindiendo de la constante numérica 2, lo cual es una práctica usual cuando lo que se busca son estimaciones del orden de magnitud y no los valores precisos de una cantidad) del orden de :
GM/c²
Igualando esta cantidad con la longitud de onda Compton mp, obtenemos la relación aproximada para la masa de Planck que se dá en los textos:
Gmp/c² ≈ h/mpc
mp² ≈ hc/G
mp ≈ √hc/G
mp² ≈ hc/G
mp ≈ √hc/G
Planck obtuvo su fórmula por una cadena de razonamientos diferentes a los que hemos utilizado (en su tiempo no existía la Relatividad General, no había definición alguna del radio de Schwarzschild, y mucho menos se concebía la posibilidad de que pudiese haber agujeros negros), y pese a ello el haber obtenido la misma fórmula obtenida por Planck nos hace sospechar que no se trata de una mera casualidad.
Una vez que tenemos una fórmula para la masa de Planck, podemos intentar obtener una expresión correspondiente para la longitud de Planck, definiéndola como aquella longitud que para cierta masa su radio de Schwarzschild y su longitud de onda Compton tendrán los mismos valores. Esto nos conduce a la siguiente fórmula:
y cuyo valor usando las mediciones que hoy se tienen para las constantes físicas resulta ser (en la página 480 de su trabajo, Planck obtiene 4.13·10-33 centímetros):
lp = 1.616252·10-35 metros ≈ 1.6·10-35 metros
Obsérvese que, por la forma en la que está definida la longitud de Planck, no aparecen constantes de proporcionalidad, ya que las constantes físicas forma una parte integral de la definición.
PROBLEMA: A partir de la relación para la masa de Planck, obténgase la relación respectiva para la longitud de Planck.
La longitud de onda de Compton está dada por la relación:
λ = h/m0c = hc/m0c²
Por otro lado, la masa de Planck está dada por la relación:
mp = √hc/G
Haciendo mp = m0 y definiendo lp = λ, obtenemos de las dos relaciones anteriores:
lp = hc/[(√hc/G) c²]
que una vez simplificado nos conduce a la longitud de Planck.
Lo primero que destaca de la longitud de Planck, 1.6·10-35 metros, es que esta longitud está situada precisamente entre lo que vimos que era la longitud de onda Compton y el radio de Schwarzschild para un electrón. Pero esta longitud fue obtenida sin hacer referencia a ninguna partícula en especial. Es una longitud universal del orden sub-atómico. Esta distancia es de una importancia tal que se tendrá que decir algo más sobre ella antes de dar por concluída esta entrada.
Teniendo ya una unidad natural para la masa y otra unidad natural para la longitud en la escala de Planck, solo nos falta determinar una unidad natural para el tiempo, siendo esta unidad un tiempo que se conoce como el tiempo de Planck, el cual se define universalmente como igual a la longitud de Planck dividida entre la velocidad de la luz, lo cual nos conduce a la fórmula:
cuyo valor calculado resulta ser (en la página 480 de su trabajo, Planck obtiene 1.38·10-43 segundos):
tp = 5.39124·10-44 segundos
Hoy se cree que el tiempo de Planck es el momento más temprano en la historia del Universo en el cual aún trabaja nuestra física teórica. También es el intervalo de tiempo más corto de tiempo que nos será posible medir en el laboratorio con nuestros conocimientos actuales de física, y aquí nos estamos refiriendo al aspecto teórico ya que en el aspecto práctico se antoja casi imposible el poder llegar a tanta precisión).
De este modo, las tres unidades fundamentales en la escala de Planck, la longitud Planck, la masa Planck y el tiempo Planck, son el símil de las unidades de metro-kilogramo-segundo en el sistema internacional SI de unidades MKS.
Además de las unidades naturales ya mencionadas, tenemos la unidad fundamental para la carga eléctrica de Planck que hoy en día evaluamos como:
y cuyo valor calculado resulta ser:
qp = 1.875545·10-18 coulombs
Por último, la quinta unidad natural propuesta por Planck, la unidad fundamental para la temperatura de Planck que hoy en día evaluamos como:
y cuyo valor calculado resulta ser (en la página 480 de su trabajo, Planck obtiene 3.5·1032 grados Celsius):
Tp = 1.4167·1032 °K
A partir de las unidades naturales de Planck, podemos recuperar las tres principales constantes fisicas fundamentales en el sistema MKS del modo siguiente:
Velocidad de la luz = c = lp /tp
c = 1.616252·10-35 metros / 5.39124·10-44 segundos
c = 299,758,857.4
c = 1.616252·10-35 metros / 5.39124·10-44 segundos
c = 299,758,857.4
Constante de gravitación universal = G = (lp)3/[mp (tp)²]
G = (1.616252·10-35)3 /[(2.17644·10-8) (5.39124·10-44)²]
G = 0.06673·10-9
G = 6.673·10-11 m3 / kg· seg²
G = (1.616252·10-35)3 /[(2.17644·10-8) (5.39124·10-44)²]
G = 0.06673·10-9
G = 6.673·10-11 m3 / kg· seg²
Constante de Planck/2π = hbarra = h = (lp)²mp /tp
h = (1.616252·10-35)² (2.17644·10-8 ) /5.39124·10-44
h = 1.054571628·10-34 joule·segundo
h = (1.616252·10-35)² (2.17644·10-8 ) /5.39124·10-44
h = 1.054571628·10-34 joule·segundo
Se añade aquí como tema de interés que a partir de las unidades de Planck arriba citadas se pueden obtener unidades derivadas de Planck, tales como el área de Planck:
cuyo valor resulta ser:
l²p = 2.61223·10−70 metros²
o como el volumen de Planck:
cuyo valor resulta ser:
l3p = 4.22419·10−105 metros3
Del mismo modo obtenemos el momentum de Planck:
con un valor de:
mpc = 6.52485 Kg·metro /seg
y la energía de Planck:
con un valor de:
Ep = 1.9561·109 joules
Planck no sólo propuso que se adoptasen tres constantes físicas fundamentales (la constante de la gravitación universal G, la velocidad de la luz y la constante de Boltzmann) como base de un nuevo sistema de unidades naturales. También propuso que, para fines de simplificación en los desarrollos demostrativos, se les diese a todas estas constantes físicas fundamentales el valor arbitrario de 1 eliminando con ello las constantes de proporcionalidad, anticipando de este modo las unidades geometrizadas que se utilizan en la Relatividad General al darle a la velocidad de la luz el valor de 1 metro por segundo. Dándoles a la constante de gravitación universal G, a la velocidad de la luz c, a la constante de Planck y a la constante de Boltzmann k el valor adimensional de 1:
G = c = h = k = 1
entonces de inmediato tenemos que tanto la longitud de Planck, la masa de Planck, el tiempo de Planck, y la temperatura de Planck son todas iguales a la unidad:
lp = mp = tp = Tp = 1
Sobre este asunto, se puede decir que aunque se trate de un truco matemáticamente aceptable que puede que ahorre algo de trabajo y esfuerzos, a la postre se puede traducir en una pérdida de información conviritiéndose en la causa de una enorme confusión, sobre todo para aquellos que están disciplinados a trabajar desde el principo hasta el final en la resolución de problemas siguiendo dimensionalmente el orden de todas las unidades y las constantes de proporcionalidad.
Desde el aspecto positivo, el uso de las unidades naturales tal y como fueron propuestas por Planck trae consigo varias ventajas. La primera y más obvia es que simplifica mucho la estructura de las ecuaciones físicas porque elimina las constantes de proporcionalidad y hace que los resultados de las ecuaciones no dependan del valor de las constantes. También permite evitar bastantes problemas de redondeo, sobre todo en computación. Por otra parte, se pueden comparar mucho más fácilmente las magnitudes de distintas unidades. Por ejemplo, dos protones se rechazan porque la repulsión electromagnética es mucho más fuerte que la atracción gravitatoria entre ellos. Esto se puede comprobar al ver que los protones tienen una carga aproximadamente igual a una unidad natural de carga, pero su masa es mucho menor que la unidad natural de masa. Desafortunadamente, las unidades naturales tienen el inconveniente de que al usarlas es más difícil percatarse de los errores dimensionales.
Retomaremos ahora la longitud de Planck que como vimos arriba es igual a:
lp ≈ 1.6·10-35 metros
Aún suponiendo que sea posible comprimir dimensionalmente un electrón por debajo de su longitud de onda Compton de 2.43·10−12 metros, no será posible comprimirlo debajo de la longitud de Planck lp porque terminaría convirtiéndose en un agujero negro dejando de existir como electrón. Del mismo modo, regresando al caso de las dos partículas que están siendo aproximadas la una a la otra, si la longitud de Compton no fuese un obstáculo la longitud de Planck sí lo sería, y en este caso estamos hablando de un obstáculo insalvable:
A distancias comparables con la longitud de Planck, se cree que están sucediendo cosas muy curiosas que rebasan ampliamente los límites de nuestra imaginación. A diferencia de la filosofía reduccionista que propone que lo más complejo está elaborado -axiomáticamente- a partir de lo más elemental, lo que está sucediendo en la escala de Planck no parece tener nada de elemental o sencillo. Se cree que a esta escala la continuidad del espacio-tiempo en vez de ir marchando sincronizadamente al parejo con lo que vemos en el macrocosmos de hecho stá variando a grado tal que a nivel ultra-microscópico el tiempo no sólo avanza o se detiene aleatoriamente sino inclusive marcha hacia atrás, una especie de verdadera máquina del tiempo. Las limitaciones de nuestros conocimientos sobre las rarezas que puedan estar ocurriendo en esta escala en el orden de los 10-35 metros, la longitud de Planck, ha llevado a la proposición de modelos tan imaginativos y tan exóticos como la teoría de la espuma cuántica que supuestamente veríamos aún en la ausencia de materia-energía si fuésemos ampliando sucesivamente una porción del espacio-tiempo plano:
Naturalmente, a niveles ultramicroscópicos no podemos hablar de la ausencia total de materia-energía debido a las fluctuaciones del vacío predichas por la Mecánica Cuántica que permiten que en todos los ámbitos del Universo estén apareciendo partículas virtuales salidas de la nada que van desapareciendo tan rápidamente como se van creando. La imagen de una “espuma cuántica”, propuesta inicialmente en 1955 por John Archibald Wheeler para describir cualitativamente las turbulencias que se supone ocurren en el espacio-tiempo sub-atómico a distancias pequeñas del orden de la longitud de Planck, han sido avaladas por físicos de la talla de Roger Penrose en su libro The Road to Reality:
Estas turbulencias que en realidad son turbulencias en la fábrica del Universo, turbulencias en el espacio-tiempo y en la materia-energía que llegan a confundirse en los niveles ultra-microscópicos, supuestamente pueden aflorar y se pueden conectar y desconectar entre sí superando incluso lo que ocurre con la espuma de las olas del mar:
aunque todas estas descripciones reflejan más una abundante imaginación que un hecho existencial apoyado teóricamente con alguna hipótesis que pueda ser comprobada en el laboratorio sobre hechos que están más allá de poder ser medidos jamás en algún laboratorio construído por humanos. La única forma de confrontar la factibilidad o la posibilidad del modelo de la espuma cuántica nos lleva necesariamente a confrontar la carencia de un modelo que logre unificar exitosamente al macrocosmos con el microcosmos, a la Relatividad General con la Mecánica Cuántica, la Gravedad Cuántica. Si la energía y la materia (o mejor dicho la masa-energía) están discretizadas, se supone que también deben de estarlo el espacio y el tiempo (o mejor dicho, el espacio-tiempo), y la “partícula fundamental” del espacio-tiempo debe de serlo el gravitón, aunque de momento todo esto son especulaciones que seguirán siéndolo mientras no tengamos a la mano algo que pueda confirmar la existencia de tan exótica partícula, quizá la más exótica de cuantas hayan sido concebidas por la imaginación del hombre.
La longitud de onda del gravitón (si es que existe) estaría dada esencialmente por la misma fórmula para la longitud de onda Compton que ya vimos anteriormente:
y el radio del gravitón bosón a su vez estaría dado por la relación:
Pero estas dimensiones hasta la fecha siguen siendo conjeturas, ya que no hay laboratorio en el mundo que sea capaz de poder medirlas.
Las escalas de Planck nos indican el límite en el cual las propiedades cuánticas de cualquier partícula producirán una perturbación significativa en la métrica del espacio-tiempo, precisamente el límite en el cual nos tenemos que preocupar por reconciliar la Relatividad General con la Mecánica Cuántica. En comparación con las elevadas energías que pueden ser alcanzadas con el Gran Colisionador de Hadrones (Large Hadron Collider ó LHC), la masa de Planck de
mp = 1.220862·1019GeV/c²
es enorme, reflejando el hecho de que la fuerza gravitatoria entre las partículas elementales es muy débil en comparación con las otras fuerzas del orden atómico que conocemos, y esto es lo que hace improbable que alguna vez podamos observar experimentalmente los efectos de la gravedad cuántica, máxime que la única ocasión en la que se han de haber producido tales energías en el Universo fue cuando el mismo Universo nació en medio de una gran explosión.
El papel original de Planck
El documento con el cual Max Planck introdujo sus escalas (él no las llamó “escalas de Planck”) que proféticamente anticiparon varias de las limitaciones en las cuales actualmente se encuentra atorado el alcance de nuestros conocimientos se encuentra disponible, en alemán, en el siguiente enlace:
http://bibliothek.bbaw.de/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=10-sitz/1899-1&seite:int=454