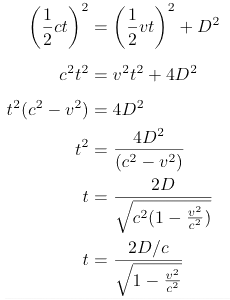Empezaremos con el siguiente ejemplo que es tal vez uno de los ejemplos más simples que podamos concebir, en el cual tenemos a un experimentador viajando en un tren sin paredes y sin techo, con la plataforma descubierta, a una velocidad extremadamente alta de 100 mil kilómetros por segundo con respecto a las vías del tren, el cual con una linterna acciona un rayo de luz que en el dibujo podemos ver que viaja de izquierda a derecha:
En la tierra tenemos un observador que ve pasar rápidamente al vagón a la velocidad de 100 mil kilómetros por segundo.
El viajero que va en el tren con la plataforma al descubierto y el cual tiene una linterna reposando en sus manos, ve salir al rayo de luz de la linterna con una velocidad de 300 mil kilómetros por segundo. Si tiene instrumentos a bordo esto es lo que él medirá.
¿Y qué velocidad medirá para el mismo rayo de luz el observador que ve pasar el vagón a una velocidad de 100 mil kilómetros por segundo? Nuestro sentido común nos dice que la velocidad del rayo de luz de 300 mil kilómetros por segundo se sumará a la velocidad del vagón de 100 mil kilómetros por segundo resultándole en una velocidad de 400 mil kilómetros por segundo. Pero la Teoría de la Relatividad nos dice que él también medirá una velocidad de 300 mil kilómetros por segundo para el rayo de luz. Ambos miden para el mismo rayo de luz una velocidad de 300 mil kilómetros por segundo. ¿Entonces qué es lo que está sucediendo? Lo que está sucediendo es que la distancia que recorre el rayo de luz para el experimentador que viaja en el vagón y el tiempo que tarda en recorrer dicha distancia son diferentes del tiempo y de la distancia que el observador en tierra mide experimentalmente. En efecto, las distancias y los tiempos han dejado de ser unidades de medición absolutas. Lo único que no ha cambiado y que permanece invariable como una constante universal es ese rayo de luz.
Consideremos ahora otro experimento hipotético, en el cual tenemos un ferrocarril que se mueve a una velocidad extremadamente rápida, dentro del cual hay un pasajero A que tiene una linterna en su mano y que en un momento dado enciende y apaga su linterna con el objeto de enviar un pulso luminoso hacia un espejo que puede estar situado ya sea en el techo del vagón en el que viaja o en la pared contraria, siempre y cuando el pulso luminoso no sea enviado en la misma dirección en la cual se está moviendo el tren o en dirección contraria, sino en una dirección perpendicular al sentido del movimiento del tren.

Supondremos también que hay un observador externo B situado a un lado de las vías del ferrocarril que se ha puesto de acuerdo previamente con el viajero A en el tren en que el observador externo B es el que está en reposo y que el tren se está moviendo a una velocidad V de 0.6 metros por segundo. Puesto que la velocidad de la luz es extremadamente alta, para fines didácticos consideraremos una velocidad de la luz c igual a un metro por segundo, lo cual no altera las conclusiones básicas que estamos buscando.
Es ya costumbre “encajonar” al viajero que se traslada en la plataforma móvil dentro de lo que llamamos un marco de referencia (la palabra inglesa es reference frame) como si estuviese contenido dentro del marco de un cuadro en el cual está todo lo que se mueve junto con el viajero incluyendo al tren, su linterna, el aire que respira, el espacio tridimensional en el que está situado, en fin, todo incluyéndolo a él; como también es ya costumbre denotar dicho marco de referencia con la letra S'. Por otro lado, es ya costumbre “encajonar” el observador situado a un lado de las vías del ferrocarril y al cual consideramos en reposo dentro de su propio marco de referencia como también es ya costumbre denotar dicho marco de referencia con la letra S:
El viajero A lleva consigo dentro de su marco de referencia (que llamaremos S' siguiendo la costumbre usual) un reloj electrónico de alta precisión con el cual mide el tiempo total de ida y vuelta que el pulso luminoso tarda en recorrer la distancia D de la linterna hasta el espejo junto con el tiempo que tarda en regresar a su punto de origen. El tiempo que transcurre entre dos eventos que ocurren dentro de un mismo marco de referencia en el cual el observador está en reposo es conocido como tiempo propio (y también como tiempo local).
Para fines ilustrativos usando números, supondremos que la distancia D del viajero hasta el espejo que tiene frente a él es de 4 metros. Entonces el pulso luminoso recorrerá un total de 8 metros en su trayecto de ida y vuelta:
Entonces el tiempo propio Δt' que mide el viajero con su reloj entre la salida del pulso de luz de la linterna y el retorno del pulso después de haber sido reflejado por el espejo será igual a:
c = 2D / Δt'
Δt' = 2D / c
Δt' = 8 metros / 1 metro por segundo
Δt' = 8 segundos
Δt' = 2D / c
Δt' = 8 metros / 1 metro por segundo
Δt' = 8 segundos
Sin embargo, lo que observa el viajero dentro de su marco de referencia S' no es lo mismo que lo que observa la persona que está fuera del ferrocarril a un lado de las vías del tren en un marco de referencia que llamaremos S, la cual verá al pulso de luz recorrer una longitud mayor que la que ve el viajero dentro del vagón:
Si el ferrocarril se está trasladando a una velocidad V igual a 0.6 metros por segundo, entonces la distancia L recorrida por el pulso luminoso será indudablemente mayor para el observador estacionario en el marco de referencia S que la distancia 2D que el viajero ve que el pulso luminoso recorre en su marco de referencia S'. Sin embargo, por el segundo postulado de la Teoría Especial de la Relatividad, ambos deben medir la misma velocidad c para ese pulso luminoso. Entonces, ¿cómo puede el observador estacionario obtener la misma velocidad c para el pulso luminoso siendo que la longitud de recorrido que él mide es mayor que la longitud de recorrido para el viajero dentro del vagón? Pues midiendo un tiempo mayor de recorrido Δt para el pulso luminoso que el tiempo Δt' medido por el viajero A. Este es un fenómeno relativista conocido como la dilatación del tiempo.
Usando el Teorema de Pitágoras, el recorrido del rayo de luz se puede descomponer en una componente vertical y una componente horizontal:
Veamos ahora las cosas desde la perspectiva del observador externo B, en el marco de referencia S, medidas en el tiempo propio del observador externo B.
Para el observador B, el rayo de luz hace un recorrido triangular que, dentro de su marco de referencia, transcurre en un tiempo total Δt que necesariamente debe ser mayor que el tiempo propio Δt' del viajero A para que así ambos puedan medir para el rayo de luz la misma velocidad c. En algo en lo que ambos viajero y observador externo están completamente de acuerdo, además del hecho de que los dos miden para el pulso luminoso la misma velocidad c, es que el tren se está desplazando a la misma velocidad V de 0.6 metros por segundo.
En su tiempo Δt, entre ambos eventos del disparo y retorno del rayo de luz a su punto de origen, para el observador B el tren habrá avanzado una distancia total VΔt. Entonces la distancia que habrá avanzado el tren desde que el rayo de luz es disparado por el viajero A hasta que llega al espejo situado en el lado contrario al viajero será la mitad, o sea (VΔt)/2. También, en su marco de referencia S, el observador B medirá para la distancia total recorrida por el rayo de luz desde que es disparado por el viajero A hasta que regresa a su punto de origen una longitud total de cΔt. Entonces la distancia que habrá recorrido el rayo de luz desde que es disparado por el viajero A hasta que llega al espejo situado en el lado contrario al viajero será la mitad de la trayectoria total, o sea (cΔt)/2). Podemos ver que la relación de longitudes, de acuerdo con el teorema de Pitágoras, estará dada en base al siguiente triángulo:
y será:
(cΔt/2)² = D² + (VΔt/2)²
Entonces, despejando para Δt:
Δt = 2D/√ c² - V²
Δt = (8 metros)/√(1 metro/seg)² - (0.6 metro/seg)²
Δt = 8/0.8 segundos
Δt = 10 segundos
Así pues, para el observador B, el rayo de luz tarda 10 segundos en recorrer el trayecto total de ida y vuelta. El tiempo que mide el viajero A se ha dilatado (expandido) en B, ya que el viajero B mide 8 segundos entre ambos eventos. Al usar la palabra “dilatación”, no la estamos utilizando en el sentido de “retraso”, “dilación”, sino en el sentido de “aumento”, “expansión”.
Δt = (8 metros)/√(1 metro/seg)² - (0.6 metro/seg)²
Δt = 8/0.8 segundos
Δt = 10 segundos
Así pues, para el observador B, el rayo de luz tarda 10 segundos en recorrer el trayecto total de ida y vuelta. El tiempo que mide el viajero A se ha dilatado (expandido) en B, ya que el viajero B mide 8 segundos entre ambos eventos. Al usar la palabra “dilatación”, no la estamos utilizando en el sentido de “retraso”, “dilación”, sino en el sentido de “aumento”, “expansión”.
Usando exactamente el mismo procedimiento que el que utilizamos para resolver este problema numérico, podemos obtener una fórmula general para la dilatación del tiempo (en la derivación de la fórmula se prescindirá del símbolo Δ al sobreentenderse que el tiempo t es una diferencia de tiempo transcurrido entre dos eventos):
Pero ya vimos que 2D/c es el tiempo t' que mide el viajero A entre ambos eventos. Entonces:

Usando los valores del numéricos del ejemplo, con V=0.6 metros/segundo y Δt' = 8 segundos, encontramos que el tiempo del viajero A se dilata a un tiempo Δt de 10 segundos, lo cual nos verifica la fórmula.
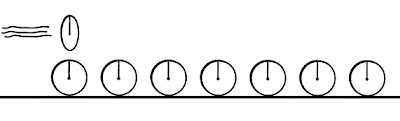
Supongamos ahora que tenemos en tierra espaciados a distancias iguales una serie de relojes sincronizados que están en reposo cada uno de ellos con respecto a todos los demás:
Al referirnos a estos relojes como relojes sincronizados estamos hablando de relojes que no sólo marcan todos ellos la misma hora para el observador en reposo situado en tierra sino que también avanzan a la par cada uno de ellos con respecto a los demás sin adelantarse ni retrasarse.
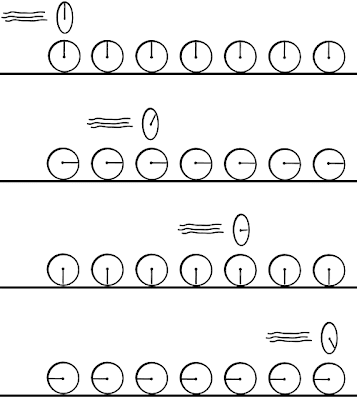
Si repetimos los cálculos que hemos hecho arriba manteniendo constante (igual) la velocidad V usando trayectorias de recorrido más largas, comprobaremos que el tiempo dilatado Δt aumentará en forma directamente proporcional al tiempo propio Δt' medido dentro del vagón. O sea que si el reloj Δt' marca 8 segundos justo cuando un reloj del observador enfrente de él marca un tiempo Δt de 10 segundos, entonces si el reloj Δt' marca 16 segundos (el doble) entonces otro reloj en tierra que se encuentre directamente enfrente de él al tomarse la lectura estará marcando un tiempo Δt de 20 segundos, y si el reloj Δt' marca 24 segundos (el triple) entonces otro reloj en tierra que se encuentre directamente enfrente de él al tomarse la lectura estará marcando un tiempo Δt de 30 segundos, en una forma sugerida por las siguientes figuras (los relojes sincronizados puestos a lo largo del sistema de referencia del observador en reposo se mantienen sincronizados en todo momento para el observador en reposo; sin embargo y como lo veremos posteriormente, todos esos relojes aparecerán desincronizados para el observador en movimiento al ocurrir una pérdida relativista de la simultaneidad absoluta con la cual lo que es simultáneo en un marco de referencia deja de serlo al ser visto desde otro marco de referencia):
Todo esto nos indica que el factor de corrección (que en este caso es igual a Δt/Δt' = 10/8 = 1.25) que debemos aplicar para obtener el tiempo en el marco de referencia en tierra Δt cuando conocemos el tiempo Δt' dentro del vagón es una cantidad constante, y por lo tanto la transformación matemática requerida para pasar del marco de referencia del vagón al marco de referencia en tierra (o viceversa) debe ser una transformación linear. Haremos uso de esta observación cuando posteriormente llevemos a cabo la derivación de fórmulas de carácter general para poder movernos de un marco de referencia a otro.
Analicemos ahora el ejemplo desde la perspectiva del viajero A estando ambos todavía de acuerdo en que el viajero A es el que se está desplazando a una velocidad V y el observador B está en reposo.
Supongamos ahora que tenemos en tierra espaciados a distancias iguales una serie de relojes sincronizados que están en reposo cada uno de ellos con respecto a todos los demás:
Al referirnos a estos relojes como relojes sincronizados estamos hablando de relojes que no sólo marcan todos ellos la misma hora para el observador en reposo situado en tierra sino que también avanzan a la par cada uno de ellos con respecto a los demás sin adelantarse ni retrasarse.
Si repetimos los cálculos que hemos hecho arriba manteniendo constante (igual) la velocidad V usando trayectorias de recorrido más largas, comprobaremos que el tiempo dilatado Δt aumentará en forma directamente proporcional al tiempo propio Δt' medido dentro del vagón. O sea que si el reloj Δt' marca 8 segundos justo cuando un reloj del observador enfrente de él marca un tiempo Δt de 10 segundos, entonces si el reloj Δt' marca 16 segundos (el doble) entonces otro reloj en tierra que se encuentre directamente enfrente de él al tomarse la lectura estará marcando un tiempo Δt de 20 segundos, y si el reloj Δt' marca 24 segundos (el triple) entonces otro reloj en tierra que se encuentre directamente enfrente de él al tomarse la lectura estará marcando un tiempo Δt de 30 segundos, en una forma sugerida por las siguientes figuras (los relojes sincronizados puestos a lo largo del sistema de referencia del observador en reposo se mantienen sincronizados en todo momento para el observador en reposo; sin embargo y como lo veremos posteriormente, todos esos relojes aparecerán desincronizados para el observador en movimiento al ocurrir una pérdida relativista de la simultaneidad absoluta con la cual lo que es simultáneo en un marco de referencia deja de serlo al ser visto desde otro marco de referencia):
Todo esto nos indica que el factor de corrección (que en este caso es igual a Δt/Δt' = 10/8 = 1.25) que debemos aplicar para obtener el tiempo en el marco de referencia en tierra Δt cuando conocemos el tiempo Δt' dentro del vagón es una cantidad constante, y por lo tanto la transformación matemática requerida para pasar del marco de referencia del vagón al marco de referencia en tierra (o viceversa) debe ser una transformación linear. Haremos uso de esta observación cuando posteriormente llevemos a cabo la derivación de fórmulas de carácter general para poder movernos de un marco de referencia a otro.
Analicemos ahora el ejemplo desde la perspectiva del viajero A estando ambos todavía de acuerdo en que el viajero A es el que se está desplazando a una velocidad V y el observador B está en reposo.
El viajero A mide para el rayo de luz en su plataforma móvil con su reloj en mano una velocidad de c = 1 metro por segundo al recorrer dentro de su marco de referencia una distancia total (ida y vuelta) de 8 metros en 8 segundos. Pero al ser reflejado el rayo de luz y llegar a su punto de origen, encuentra que en ese mismo punto en el que ambos coinciden por un instante mientras el tren prosigue con su movimiento el reloj del observador B marca 10 segundos. Ambos siguen en completo acuerdo en que el tren se está moviendo a la misma velocidad V con respecto a ambos. La única forma posible en la que el viajero A pueda seguirle asignando al observador B una velocidad V de 0.6 metros por segundo (en dirección opuesta) es que el viajero A determine desde su punto de vista una longitud menor para el observador B entre ambos eventos, ya que de no ser así le estaría midiendo una velocidad errónea igual a:
6 metros / 8 segundos = 0.75 metros / segundo
Entonces el viajero A también necesita un factor de corrección para compensar por la contracción de longitud que está detectando. ¿Y de cuánto tiene que ser ese factor de corrección? Para poder seguirle midiendo al observador B una velocidad de 0.6 metros por segundo en ocho segundos, la distancia entre ambos eventos en la plataforma de B según el viajero A, debe ser:
espacio = tiempo x velocidad
espacio = (8 segundos) x (0.6 metros/segundo)
espacio = 4.8 metros
espacio = (8 segundos) x (0.6 metros/segundo)
espacio = 4.8 metros
¡Para el viajero A, una longitud de 6 metros del observador B parece haberse contraído a 4.8 metros! El factor de corrección para la contracción de longitud debe ser entonces:
4.8 metros / 6 metros = 0.8
El factor de corrección utilizado por el viajero móvil A para medir la contracción de la longitud en B resulta ser exactamente el inverso del factor de corrección utilizado por el observador B para poder determinar la dilatación del tiempo de A, lo cual era de esperarse y no debe causarnos ningún asombro. Lo que para un observador es un fenómeno físico de dilatación del tiempo para el otro observador refiriéndose a los mismos eventos es un fenómeno físico de contracción de longitud.
En la cinemática relativista, la contracción de la longitud es un corolario de la dilatación del tiempo, y viceversa. Ambas cosas siempre van de la mano.
El factor de corrección:
aparece con tanta frecuencia en problemas propios de la Teoría Especial de la Relatividad, que con fines de simplificación notacional es representado con el símbolo γ (letra griega gamma):
Con esto tenemos la siguiente relación simplificada para obtener la dilatación del tiempo al pasar del marco de referencia a otro:
Si simbolizamos al tiempo propio (tiempo local) del observador en reposo con la letra griega τ (tau), entonces la fórmula toma el siguiente aspecto que resulta más familiar para quienes estudian ciertos aspectos más avanzados de la Teoría de la Relatividad:
Del mismo modo, con el factor de corrección γ podemos escribir la siguiente relación simplificada para obtener la contracción de longitud al pasar de un marco de referencia a otro:
Por otra parte, la cantidad V/c aparece también en el análisis de problemas de relatividad con tanta frecuencia que es común que sea abreviada con el símbolo β (letra griega beta):
β = V/c
Hagamos el cálculo de la velocidad del rayo de luz tal y como es medida tanto por el viajero A como por el observador B. Desde la perspectiva del viajero A, el rayo de luz recorre dentro de su marco de referencia S' ocho metros (2D) en ocho segundos (Δt'). Entonces él mide una velocidad de:
c = 2D / 2Δt'
c = (8 metros) / (8 segundos)
c = 1 metro/segundo
c = (8 metros) / (8 segundos)
c = 1 metro/segundo
Desde su perspectiva, el observador B ve que el rayo de luz recorre una distancia dentro del marco de referencia del viajero A tanto en su trayectoria de ida como en su trayectoria de regreso una distancia que podemos obtener del triángulo de las distancias básicas:
Podemos ver que para el observador B el rayo en su trayectoria de ida recorre 5 metros, o sea que en su trayectoria total de ida y vuelta recorre 10 metros. Entonces para el observador B el rayo de luz tiene una velocidad de:
c = 10 metros / Δt
c = 10 metros / 10 segundos
c = 1 metro/segundo
c = 10 metros / 10 segundos
c = 1 metro/segundo
Ambos viajero A y observador B miden para el rayo de luz la misma velocidad, como era de esperarse.
Como lo hemos visto, la parte matemática del problema no es tan difícil de resolver. Lo duro viene al considerar la parte filosófica. Cuando hablamos de contracción de longitud, ¿de qué estamos hablando realmente? ¿Se comprime una vara de medir conforme pasa volando a gran velocidad frente a nosotros? ¿Qué la comprime?
En realidad, la vara de medir en sí no se comprime. Es todo el espacio que viaja en ella y en torno a ella el que se achica. Se achica el espacio entre los átomos de la vara de medir, se achica longitudinalmente el cuerpo del observador B, absolutamente todo se achica, y es precisamente por ello que el observador B no percibe cambio alguno en su marco de referencia dentro del cual para él todo sigue igual sin contracción alguna.
De las fórmulas obtenidas, podemos ver que entre mayor sea la velocidad V del viajero A tanto mayor será la contracción de longitud que el viajero a detecta en todo lo que corresponde al espacio del observador estacionario B. Si le fuera posible al viajero moverse a la velocidad de la luz, entonces de acuerdo con la fórmula todo el espacio del observador B desaparecería longitudinalmente, desaparecería del Universo, lo cual ciertamente no va a ocurrir. Ningún objeto material sólido puede moverse a una velocidad igual o mayor que la velocidad de la luz. Sólo la luz puede moverse a la velocidad de la luz, y la luz no es ningún objeto material sólido, es energía electromagnética pura.
Es importante enfatizar que lo que hemos visto no es una cuestión de ilusiones ópticas. Se trata de fenómenos reales que están ocurriendo en el mundo real. No nos damos cuenta de ello porque siendo la velocidad de la luz extremadamente alta, el factor V²/c² y con ello el factor de corrección sólo se vuelve importante para situaciones que se acercan a la velocidad de la luz. Pero los efectos son medibles. Un caso que ocurre cotidianamente tiene que ver con las partículas cósmicas que constantemente están bombardeando la Tierra. Al chocar contra la atmósfera de la Tierra, cada una de las partículas cósmicas produce una estela de otras partículas subatómicas:
En el siguiente dibujo podemos ver una representación de las partículas subatómicas que una partícula cósmica produce tras su choque con la atmósfera terrestre:
Entre todas estas partículas subatómicas hay una que nos interesa, el muón μ+, producido por el decaimiento del mesón π+ a su vez producido por el choque de la partícula cósmica con la atmósfera terrestre. Por experimentos llevados a cabo en laboratorios en la Tierra, se sabe que los muones cuando están reposo tienen un tiempo de vida medio de tan sólo 2 microsegundos, un tiempo extremadamente corto. Puesto que los muones son producidos a gran altura, muy pocos de ellos deberían llegar al nivel del mar. Sin embargo, los muones que se observan son muchos (esto se puede confirmar utilizando una cámara de niebla de Wilson). Un muón viajando a una velocidad de 0.99 veces la velocidad de la luz (0.99c) alcanzaría a recorrer únicamente unos 600 metros en sus 2.2 microsegundos de vida. Sin embargo, en virtud de que el muón viaja a una velocidad muy cercana a la velocidad de la luz, en el marco de referencia del muón el tiempo avanza mucho más lentamente. Su vida media de 2.2 microsegundos se ve incrementada en el marco de referencia de la Tierra por un factor de corrección de 16 (para una velocidad de 0.998c), aumentando hasta 16 microsegundos, y un muón viajando a la velocidad de 0.99c alcanza a recorrer 4,800 metros en este lapso de tiempo:
Sin embargo, desde la perspectiva del muón, viajando a un lado suyo, su vida media sigue siendo de 2.2 microsegundos. Lo que pasa es que la distancia que recorre el muón es menor por los efectos de la contracción relativista de la longitud. El muón no recorre los 4,800 metros, recorre únicamente 600 metros:
Nuevamente, lo que para un observador se trata de una dilatación del tiempo, para el otro observador se trata de una contracción de longitud.
PROBLEMA: En su primer papel en el cual dió a conocer al mundo su Teoría Especial de la Relatividad, Einstein escribió lo siguiente:
“Si en los puntos A y B de K hay relojes estacionarios que, vistos desde un sistema estacionario, están sincronizados, y si el reloj en A es movido con velocidad V a lo largo de la línea AB hacia B, entonces a su llegada a B los dos relojes no sincronizarán, el reloj movido de A hacia B estará detrás del otro que permaneció estacionario por ½ tV²/c² (hasta magnitudes de orden cuatro y mayor), siendo t el tiempo ocupado en la jornada de A hacia B.”Demostrar el enunciado anterior.
Al estar en la posición A, ambos relojes que llamaremos el reloj 1 y el reloj 2 coinciden en un mismo tiempo t1 = t2. Al llegar el reloj viajero 1 de A a B, ambos relojes habrán acumulado tiempos diferentes t1 ≠ t2, y la diferencia Δt acumulada entre ambos estará dada por la fórmula para la dilatación del tiempo:
Δt = Δt’ / √ 1 - V²/c²
Δt = Δt’ { 1 - (V/c)² }-½
Δt = Δt’ { 1 - (V/c)² }-½
Podemos llevar a cabo la expansión por series de la expresión anterior recurriendo al teorema del binomio que en su forma más general es enunciado de la siguiente manera:
(a + x) n =
an + nan-1x + {n(n-1)/2!} an-2x² + {n(n-1)(n-2)/3!} an-3x3 + ...
an + nan-1x + {n(n-1)/2!} an-2x² + {n(n-1)(n-2)/3!} an-3x3 + ...
Haciendo a=1 y tomando el exponente n como el exponente fraccionario negativo -½, tenemos la serie infinita:
(1 - x) -½ = 1 + (½) x + ... __para x ≤ 1
con la cual:
Δt = Δt’ { 1 + (½) (V/c)² + O(V/c)4 }
en donde O(V/c)4 significa “los Otros términos residuales de la serie infinita sobre V/c de orden 4 o mayor”. Entonces, despreciando esos otros términos residuales de la serie:
Δt = Δt’ { 1 + (½) (V/c)² }
Δt = Δt’ + Δt’ (½) (V/c)²
Δt - Δt’ = (½) Δt’ (V²/c²)
Δt = Δt’ + Δt’ (½) (V/c)²
Δt - Δt’ = (½) Δt’ (V²/c²)
Pero Δt - Δt’ es precisamente la diferencia entre los lapsos de tiempos Δt y Δt’ transcurridos entre los dos relojes, y como el lapso de tiempo Δt’ corresponde al reloj que se movió, vemos que esto será igual a la expresión dada por Einstein en su papel original.
PROBLEMA: En el mismo papel elaborado por Einstein en donde aparece lo anterior, Einstein agregó lo siguiente:
“Entonces concluímos que un reloj de balanza puesto en el Ecuador deberá correr más lentamente, por una cantidad muy pequeña, que un reloj precisamente similar situado en uno de los polos bajo condiciones de otra manera idénticas.”Calcúlese la diferencia de tiempos entre los dos relojes después de un siglo.
En medidas angulares, la Tierra gira sobre su propio eje 2π radianes en 24 horas. Su velocidad angular ω será entonces:
ω = 2π radianes / 24 horas
ω = 72.722 · 10-6 radianes/seg
ω = 72.722 · 10-6 radianes/seg
Tomando el radio medio de la Tierra como R = 6.37 · 106 metros, podemos estimar una velocidad tangencial en su ecuador igual a:
V = ωR
V = (72.722 · 10-6 radianes/seg)(6.37 · 106 metros)
V = (72.722 · 10-6 radianes/seg)(6.37 · 106 metros)
V = 463.24 metros/seg
El retardo de tiempo acumulado después de un siglo por el reloj que avanza a la anterior velocidad V será:
t = (½) t’ (V²/c²) = (½) t’ (V/c)²
t = (½) (100 años) {(463.24 metros/seg) / (3 · 108 metros/seg)}²
t = 3.8 · 10-3 segundos
t = (½) (100 años) {(463.24 metros/seg) / (3 · 108 metros/seg)}²
t = 3.8 · 10-3 segundos
Esta es una diferencia de tiempos muy pequeña que en los tiempos de Einstein era indetectable. Sin embargo, en los tiempos de hoy en los que contamos con relojes de precisión atómica, el experimento se puede llevar a cabo en cualquier momento subiendo a una persona a un avión llevando consigo un reloj de alta precisión. El experimento ya se ha efectuado, y los resultados son precisamente los que predice la Teoría de la Relatividad. Fue llevado a cabo por vez primera en 1971 por Joseph C. Hafele y R. Keating, los cuales se subieron con cuatro relojes atómicos de cesio a bordo de aviones comerciales dándole la vuelta a la Tierra primero en dirección Este y después haciendo otro viaje redondo en dirección Oeste, comparándose las lecturas de los mismos con la lectura de otro reloj idéntico en Tierra en la ciudad de Washington sincronizado inicialmente con los relojes viajeros. Al comparar las lecturas de los relojes atómicos después del viaje, los del avión y el de la Tierra, ya no estaban sincronizados. Los relojes atómicos que habían volado estaban ligeramente retrasados (muy ligeramente pero medible con dichos relojes, la diferencia de tiempos era de unas pocas centésimas de milésima de millonésima de segundo). Tras descontar ciertos efectos gravitatorios secundarios, y asumiendo que no hubo ningún error de medida, lo cual se comprobó controlando las condiciones y repitiendo el experimento varias veces, se concluyó que la única explicación posible venía por la Teoría de la Relatividad.
A un costo de 8 mil dólares por el experimento, de los cuales 7 mil 600 dólares fueron empleados para pagar los pasajes, la edición de septiembre de 1972 de la revista Scientific American
lo llamó la prueba más económica que se haya hecho sobre la relatividad. De hecho, son tantas las pruebas experimentales que se han llevado a cabo ya de diversas maneras confirmando las predicciones teóricas de la Teoría de la Relatividad, que un resultado negativo causaría en estos momentos una verdadera conmoción entre la comunidad científica.
En tiempos recientes, los efectos relativistas de la dilatación del tiempo ocasionados por una rotación alrededor de la Tierra tienen que ser tomados en cuenta para hacer las correcciones numéricas necesarias para poder mantener sincronizados con la Tierra a los 24 satélites utilizados por el Sistema de Posicionamiento Global ó Global Positioning System (GPS), cada uno de los cuales le dá una vuelta completa a la Tierra cada 12 horas:
en virtud de que dichos satélites, al estarse moviendo en el espacio en relación con los relojes atómicos que están en reposo en la Tierra, registran un tiempo que camina con mayor lentitud. El sistema de localización GPS requiere para su buen funcionamiento que los satélites estén sincronizados a un elevado nivel de precisión, lo cual es absolutamente necesario para permitirle a las personas en la Tierra que tengan receptores GPS (cada vez incorporados con mayor frecuencia como una función en teléfonos celulares de alto costo):
el poder ubicar sus coordenadas geográficas con la exactitud requerida en base a las distancias de cada uno de los satélites cuyas señals alcanzan a llegar a un receptor de señales GPS. Aunque el efecto relativista es relativamente pequeño, los relojes atómicos son lo suficientemente precisos como para ser afectados por el efecto de la dilatación del tiempo, y las correcciones numéricas que se tienen que hacer son precisamente las que predice la Teoría de la Relatividad.
PROBLEMA: Una vara en movimiento de longitud L forma un ángulo θ con respecto a la horizontal. Si la vara se mueve a una velocidad V a lo largo de la dirección con respecto a la cual forma dicho ángulo, ¿cuál será la longitud de la vara y cuál será el ángulo que forma la vara con respecto a la horizontal para un observador en reposo que los ve pasar?
Puesto que las dimensiones de un objeto experimentan una contracción relativista por un factor √ 1 - V²/c² en la dirección del movimiento, para un observador en reposo la componente horizontal de la vara habrá quedado reducida a una longitud de:
L cos(θ) √ 1 - V²/c²
mientras que la componente de la vara perpendicular a la dirección del movimiento, que es Lsen(θ), permanecerá inalterada en ambos marcos de referencia. Por lo tanto, para el observador en reposo en el marco de referencia S, por el teorema de Pitágoras la longitud de la vara L en su marco de referencia será igual a la raíz cuadrática de la suma de los cuadrados de la componente vertical y de la componente horizontal contraída :
L² = L² sen²(θ) + (1 - V²/c²)(L² cos²(θ))
L = L √ sen²(θ) + cos²(θ)/γ²
L = L √ sen²(θ) + cos²(θ)/γ²
Y en lo que al ángulo respecta, el ángulo θ medido por el observador en S estará dado de:
Tan(θ) = [L sen(θ)]/[(L cos(θ))(√ 1 - V²/c²)]
Tan(θ) = γ Tan(θ)
θ = Tan-1[γ Tan(θ)]
Tan(θ) = γ Tan(θ)
θ = Tan-1[γ Tan(θ)]
PROBLEMA: Dos observadores en los sistemas de referencia S y S’ sincronizan sus relojes para que den las mismas lecturas de t = 0 en sus orígenes cuando coinciden el uno frente al otro. El observador en S lee la lectura del reloj en S’ a través de un telescopio. ¿Cuál es el tiempo que lee del reloj en S’ cuando su reloj marca 20 minutos si V² = (8/9) c²?
Este problema ilustra una complicación adicional que tenemos que tomar en cuenta en la resolución de ciertos problemas que tiene que ser agregada a los efectos propios de la relatividad: el tiempo finito empleado por la luz en llegar de un lugar a otro. Si nosotros desde la Tierra vemos con un telescopio un reloj en el planeta Marte sincronizado con el nuestro cuando los planetas están más cercanos, podemos tener la seguridad de que la lectura que veremos en el reloj de Marte con la ayuda de nuestro telescopio no será igual a la de nuestro reloj ya que la distancia que tiene que recorrer viajando a la velocidad de la luz la imagen del reloj es de unos 100 millones de kilómetros, y puesto que esa imagen no nos llega instantáneamente sino que es una imagen que tarda (100,000,000 Km)/(300,000 Km/seg) = 333 segundos = 6 minutos, la lectura que veremos es una imagen del pasado, de algo que nos fue enviado 6 minutos antes y que tardó 6 minutos en llegarnos. De hecho, todo, pero absolutamente todo lo que vemos, son imágenes del pasado. No hay imagen alguna de nada que vemos con nuestros ojos que nos llegue instantáneamente, inclusive de objetos cercanos a nosotros al alcance de nuestras manos, en virtud de la velocidad finita de la principal portadora de información, la luz. Vivimos en la ilusión de que todo lo que tenemos ante nosotros cerca de nosotros lo vemos justo cuando está ocurriendo, pero ello es una ilusión encubierta por el hecho de que las diferencias en los tiempos involucrados son tan pequeñas que para fines prácticos pueden ser consideradas despreciables, pero no son despreciables. Afortunadamente, aunque la velocidad de la luz es finita, también es bastante elevada, de modo tal que no nos damos cuenta de que las imágenes que vemos en torno nuestro son imágenes de un pasado tanto mayor cuanto mayor sea la distancia que nos separa de lo que estamos viendo. En estos momentos vemos con nuestros telescopios, incluído el telescopio espacia Hubble, las imágenes de estrellas que ya no existen, que se apagaron hace millones de años. En el tiempo en que tardaron las imágenes de esas estrellas en llegarnos tales estrellas desaparecieron y ya no existen “hoy”.
Regresando al problema que nos ocupa, podemos ver que ocurren tres eventos:
1) Los dos observadores S y S’ están el uno frente al otro sincronizando sus relojes a un tiempo t = t = 0.
2) El observador viajero S’ llega a cierto punto en su recorrido desde donde le envía una imagen de su reloj al observador en S.
3) La imagen del reloj de S’ le llega al telescopio al observador en S a la vez que S’ continúa su recorrido.
Nótese que el tiempo de S’ que lee el observador en S no es la lectura que está marcando el reloj de S’ cuando le llega la imagen del reloj a S a los 20 minutos.
Desde la perspectiva del observador en reposo, el tiempo de 20 minutos en el cual el observador en S recibe la imagen del reloj de S’ debe ser igual al tiempo t1 (= L/V) que tarda el viajero en S’ en llegar hasta el punto desde el cual le envía a S la imagen de su reloj, más el tiempo t2 (= L/c) que tarda en llegarle dicha imagen a S, siendo L la distancia propia medida por S:
20 minutos = t1 + t2
20 minutos = L/V + L/c = (1/V + 1/c) L’ = (√9/8 + 1) L/c = (2.06) L/c
L = (1,200 seg) (3·108 metros/seg) / 2.06 = 1.747·1011 metros
20 minutos = L/V + L/c = (1/V + 1/c) L’ = (√9/8 + 1) L/c = (2.06) L/c
L = (1,200 seg) (3·108 metros/seg) / 2.06 = 1.747·1011 metros
Esta es la distancia que ha recorrido S’ medida por S cuando el primero le envía la imagen de su reloj a S.
Sin embargo, para S’ esta distancia de está contraída por un factor
√ 1 - V²/c² = √ 1 - (8/9) = 1/3
O sea que, desde su perspectiva, S’ ha recorrido una distancia de L’ = 0.582·1011 metros. Entonces el tiempo t’ que S tiene acumulado en su reloj al recorrer dicha distancia viajando a una velocidad de V = √(8/9) c es:
t’ = L’/V = (0.582·1011 metros) / (0 2.8284·108 metros/seg)
t = 205.8 segundos = 3.43 minutos
t = 205.8 segundos = 3.43 minutos