Aunque el estudio de la Teoría Especial de la Relatividad no es un asunto complicado, el estudio de la Relatividad General presenta retos adicionales por las herramientas matemáticas que se requieren para poder desarrollar el andamiaje en el que están basados los conceptos. En otros tiempos no quedaba más remedio que confiar en el rigorismo lógico aplicado ciegamente a la obtención de resultados. Afortunadamente, en estos tiempos en los que la computadora ya no es un instrumento carísimo a la disposición de unos cuantos privilegiados, existen programas de simulación que nos permiten “ver” lo que está ocurriendo, y al poder “ver” lo que está ocurriendo estamos en mejores condiciones de poder comprender lo que está sucediendo, lo cual a su vez nos puede ayudar para generar nuevas ideas y formalizarlas sobre una estructura matemática sólida. Afortunadamente también, muchos de los programas de simulación computarizada que nos permiten experimentar sobre el monitor de la computadora con los conceptos y las ideas detrás de la Teoría de la Relatividad se pueden obtener gratuitamente sin costo alguno, sin necesidad de pagar decenas o inclusive cientos de miles de dólares.
Uno de tales programas de simulación es el que ha sido desarrollado por el grupo Open Source Physics coordinado por Wolfgang Christian, Mario Belloni y Anne Cox. El programa principal es un archivo ejecutable que puede ser abierto en cualquier máquina que tenga instalado el sistema operativo Windows (o inclusive el sistema operativo Linux), para lo cual se requiere que la máquina tenga instalada la plataforma Java que también se puede obtener gratuitamente de Internet. El archivo más conocido desarrollado por esta organización es el archivo osp_jar, el cual cuando está disponible en una computadora que tenga instalado Windows es identificable bajo el siguiente ícono propio de un archivo con la extensión .jar:
Cuando se abre dicho archivo, después de que aparece rápidamente una ventana titulada “OSP Launcher” que confirma que se está lanzando el programa principal:
se nos presenta una ventana introductoria como la siguiente:
En realidad, esta es la ventana principal que conduce a un paquete de varios programas ejecutables de los que está compuesto el paquete. Si queremos echar a andar alguno de los varios programas de simulación que incluye esta herramienta, el botón que nos interesa es el botón intermedio puesto en el borde inferior de la ventana titulado “Programs”. Si oprimimos dicho botón (haciendo clic con el ratón), se nos abre una ventana como la siguiente:
Bajo el directorio “Relativity Programs” encontramos varias opciones de simulación tales como “Newtonian Physics” (el cual nos dá la opción de llevar a cabo la simulación de casos que corresponden a la mecánica clásica pre-relativista) o como “Special Relativity” (el cual nos dá la opción de poder experimentar con situaciones que corresponden al ámbito de la Teoría Especial de la Relatividad) o como “Schwarzschild Metric” (el cual nos permite investigar lo que ocurre bajo la métrica de Schwarzschild). En la imagen de arriba tenemos seleccionada la sub-opción de “Newton Orbit” (órbita Newtoniana) que está puesta debajo de “Newtonian Physics”, y como podemos ver se nos abre una ventana interior derecha que nos dá una explicación detallada sobre el tema del que versa la simulación que se puede correr, en este caso una simulación de las órbitas que tienen los cuerpos cuando están sujetos a la atracción de una fuerza gravitatoria central.
Como podemos ver en la imagen de arriba, la sub-opción “Newton Orbit” consta a su vez de dos sub-opciones, la sub-opción “Orbits (author)” y la sub-opción “Orbits (student)”. Todos los programas de simulación nos presentan estas dos opciones. La primera sub-opción (autor) nos permite asignar valores numéricos a la fórmula con los cuales se llevará a cabo la simulación, mientras que la segunda sub-opción (estudiante) nos permite experimentar de inmediato con una simulación a la cual ya se le han asignado previamente valores numéricos a la fórmula que será simulada. Es buena idea experimentar primero con la opción del estudiante para ver qué es lo que está siendo simulado, y tras esto podemos empezar a variar algunos de los parámetros físicos con la sub-opción del autor para entender mejor la interacción de las variables. En el caso de la sub-opción “Newton Orbit” en su sub-opción “Orbits (student)”, si hacemos doble clic en el renglón que dice “Orbits (student)” se nos abrirá una ventana adicional como la siguiente:
Para echar a andar el programa de simulación, sólo tenemos que oprimir el botón “Run”. Si en cualquier momento queremos echar a andar el programa desde el principio, sólo tenemos que oprimir el botón “Reset”. Y si queremos correr el programa en pasos incrementales, podemos hacerlo oprimiendo repetidamente el botón “Step”.
En el ejemplo anterior, tenemos un programa de simulación dinámica en el cual basta con oprimir el botón “Run” para que el programa corra de manera automática sin intervención de parte nuestra. Pero hay otras simulaciones en las cuales tenemos que posicionar el cursor dentro de la ventana de trabajo e ir moviendo algún punto de anclaje de un lado a otro.
Como otro ejemplo, más en línea con la Relatividad General que con la mecánica clásica de Newton, de las simulaciones disponibles en el paquete, en la simulación que corresponde a las trayectorias de varias partículas en la vecindad de un agujero negro en rotación, accesible en la línea "Kerr Metric" en la sub-opción de N-partículas (N-Particle) y haciendo doble clic dentro de la línea "Explosion (student)", al correr la simulación con el botón de "Start" en la ventana "Control Frame" que aparece, al ir corriendo el programa tenemos una solución gráfica como la siguiente que corresponde a las trayectorias de varias partículas lanzadas:
Dentro del programa principal tenemos también una línea titulada “Rain Metric”, el cual lleva a cabo simulaciones con la métrica que corresponde al marco lluvia discutido en el texto principal de esta obra. Las simulaciones que se llevan a cabo aquí nos abren dos ventanas, la ventana titulada “Control Frame” (este es el Marco de Control desde el cual se echan a andar las simulaciones dinámicas, con el mapa de las coordenadas identificado como “Rain Map” o Mapa Lluvia, obsérvese la ausencia del agujero negro en el interior de los círculos concéntricos):
y la ventana titulada “RainBookkeeper”, como si fuese una especie de “tenedor de libros” que lleva la contabilidad de lo que ocurre en el Mapa Schwarzschild; obsérvese la presencia del agujero negro en el interior de los círculos concéntricos):
Al llevar a cabo esta última simulación, queda más claro el por qué al “marco lluvia” se le dió dicho nombre; podemos imaginarnos a todas las partículas de prueba cayendo radialmente hacia el centro del agujero negro como “gotitas de lluvia”.
En la ventana principal de entrada al programa Open Source Physics, a la izquierda del botón "Programs", hay otro botón titulado "Relativity Worksheets" (Hojas de Trabajo de Relatividad). En la ventana izquierda la línea titulada "Brief Overview" hace un repaso breve del significado de la Relatividad y a partir de la métrica de Schwarzschild obtiene expresiones para la longitud propia y el intervalo de tiempo propio en el caso gravitacional de una distribución esférica de masa, pasando a la descripción de las órbitas de partículas tanto en el caso clásico como en el caso relativista. En la misma ventana izquierda la línea "Equations and Notations" hace un resumen de las ecuaciones y la notación simbólica que es utilizada en las simulaciones computarizadas. Tras esto aparece la lista de las "Hojas de Trabajo" (Worksheets) disponibles. El programa que está siendo referenciado aquí contiene seis hojas de trabajo (worksheets) con los siguientes temas:
Hoja de Trabajo #1: Espacio
Hoja de Trabajo #2: Minimizar longitud
Hoja de Trabajo #3: Tiempo
Hoja de Trabajo #4: Orbitas Circulares en Mecánica Clásica
Hoja de Trabajo #5: Orbitas Circulares en Relatividad General
Hoja de Trabajo #6: Navegacion GPS en un agujero negro
A manera de ejemplo, dentro de la Hoja de Trabajo # 1 tenemos primero una breve introduccion, tras lo cual tenemos las opciones "Derecho en el Mapa" (Straight on the Map), "Derecho en el Espacion" (Straight in Space) y una sección de "Ejercicios". Si entramos en la opción "Straight on the Map" se nos presentan dos sub-opciones de simulación, la sub-opción para un "Espacio Plano" (Flat Space) que corresponde a un espacio-tiempo plano en donde se aplica la Teoría Especial de la Relatividad, y la sub-opción "Espacio Curvo" (Curved Space) que corresponde a un espacio-tiempo curvo en donde se aplica la Teoría General de la Relatividad. Si echamos a andar la simulación que corresponde a un espacio-tiempo plano haciendo rápidamente dos veces clic dentro de la línea que dice "Flat Space", aparecerá una ventana de simulación en la que se nos presenta un plano con coordenadas polares. Si echamos a andar la simulación que corresponde a un espacio-tiempo curvo haciendo rápidamente dos veces clic dentro de la línea que dice "Curved Space" aparecerá una ventana de simulación parecida a la anterior excepto que en el centro de la ventana de simulación tenemos un disco negro, el cual representa un agujero negro. En ambas ventanas de simulación no hay un programa dinámico que corre automáticamente, el usuario debe "tomar" cada uno de los puntos rojos y "arrastrar" cada uno de ellos dentro del mapa, con lo cual irán cambiando las lecturas de los recuadros amarillos que dan los valores en coordenadas polares de la distancia radial r así como del ángulo φ y la longitud propia del intervalo relativista σ entre los dos puntos rojos calculada por el programa de acuerdo con la fórmula relativista.
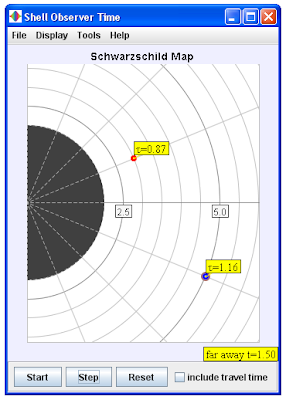
Una simulación más interesante la podemos encontrar dentro de los "Ejercicios" de la Hoja de Trabajo # 3. Haciendo doble clic rápidamente en la "Parte A", aparece no una ventana sino dos ventanas, una ventana titulada "Observed Signal" (Señal Observada) y otra ventana titulada "Shell Observer Time" (Tiempo de Observador en un Casco). La simulación muestra dos relojes, uno de color rojo situado y otro de color azul situado, ambos sincronizados inicialmente a un tiempo cero. Junto con las lecturas de los relojes y el tiempo medido desde lejos está la gráfica de la señal del reloj seleccionado y la señal recibida del otro reloj. Haciendo clic en un reloj seleccionará a dicho reloj, cambiando los datos enviados a la gráfica. La simulación es tanto interactiva como dinámica, ya que el usuario puede "arrastar" cualquiera de los dos relojes, tanto el reloj rojo como el reloj azul, a cualquier parte del mapa, y una vez posicionados los relojes en los lugares deseados se puede correr la simulación dinámica con el botón "Start". A continuación se muestran las dos ventanas con el reloj rojo posicionado en las coordenadas polares (r, θ) = (3.0, 22.6°) y con el reloj azul posicionado en las coordenadas (r, θ) = (5.0, -22.5°), con los tiempos propios de los dos relojes rojo y azul sincronizados a cero y con el tiempo medido por un observador lejano (suficientemente alejado de la influencia del campo gravitacional del agujero negro) también puesto a cero, cuando el tiempo t medido por el observador lejano es de t = 1.5 segundos:
Un sub-programa interesante desarrollado por Slavo Tuleja puesto dentro de este paquete, titulado "GROrbits", nos permite obtener gráficamente y numéricamente las órbitas de partículas de pruebas lanzadas en las afueras del plano ecuatorial tanto de un agujero negro sin rotación (Schwarzschild) como de un agujero negro en rotación (Kerr). La introducción al programa nos presenta las opciones que tenemos para cambiar las variables a nuestro antojo en la ventana principal del programa:
En los botones delizadores (sliders) a la derecha de la ventana, tenemos el botón con el cual podemos variar el parámetro J/M y el botón con el cual podemos variar el parámetro L/M. Si el parámetro J/M es positivo tenemos el graficado para un agujero negro que está en rotación en sentido contrario a las manecillas del reloj, y si el parámetro J/M es negativo tenemos el graficado para un agujero negro que está en rotación en el sentido de las manecillas del reloj. El botón deslizador L/M nos fija el potencial gravitacional efectivo en función de la distancia radial. Para un valor de J/M igual a 0.4 y un valor de L/M igual a 7.5 (los cuales se pueden obtener exactamente no con la ayuda de los botones deslizadores sino editando los valores numéricos en las líneas correspondientes en la esquina superior derecha), podemos correr la simulación de la órbita de una partícula de prueba lanzada desde una distancia radial de r = 20M y a un ángulo de 157 grados (tanto la distancia radial como el ángulo polar pueden ser verificados moviendo el cursor libremente dentro de la ventana izquierda y leyendo los valores de los mismos en la línea pequeña que aparece en la esquina inferior izquierda) cuya trayectoria es desviada por la cercanía del agujero negro que ejerce atracción gravitacional sobre la partícula pero que lleva suficiente impulso como para evitar caer en el agujero negro. La ventana resultante es una como la siguiente:
Obsérvese cómo el tiempo t medido desde la lejanía por un observador externo (suficientemente alejado de la influencia gravitacional del agujero negro) es mayor que el tiempo propio τ medido por la partícula, en concordancia con el hecho de que en presencia de un campo gravitacional el tiempo avanza más lentamente. Resulta instructivo correr el programa no en la modalidad de simulación dinámica continua sino en la modalidad de simulación "paso a paso" (step), teniendo las opciones de llevar a la partícula paso a paso hacia adelante en el tiempo o hacia atrás en el tiempo (hay dos botones "step" para ello). En la simulación "Knife edge" bajo la sub-opción "Stone" de los "Scenarios" del programa "GR Orbits" tenemos una demostración visual dramática, basada en las fórmulas de la Relatividad General, de cómo la órbita de un satélite en la cercanía de un agujero negro puede ser una órbita planetaria que a diferencia de las órbitas predichas por la ley de Newton no es una órbita elíptica cerrada sino una órbita que manifiesta una precesión. Recordemos cómo entre los primeros triunfos de la Relatividad General estuvo precisamente la explicación de la precesión de la órbita de Mercurio en torno al Sol.
La mejor forma de adquirir experiencia en este programa de simulación es experimentando con cada una de las simulaciones, al igual que la mejor forma de aprender a manejar un carro no es estudiando la teoría de los motores de combustión interna sino manejando el carro con las manos puestas al volante.
Hay otros programas de simulación puestos gratuitamente a través de Internet por la organización Open Source Physics, la cual tiene el siguiente domicilio:
http://www.opensourcephysics.org
El archivo ejecutable para los programas de demostración que se han discutido aquí fue obtenido directamente del siguiente domicilio que lleva a cabo la transferencia del archivo:
http://www.opensourcephysics.org/binary/osp_gr.jar
ESTE ES UN TRABAJO BAJO CONSTRUCCION
Seguidores
Archivo del blog
-
▼
2009
(77)
-
▼
marzo
(77)
- Indice
- Prólogo
- El movimiento absoluto
- Un descubrimiento sorprendente
- La física es parada de cabeza
- Las consecuencias directas de la teoría
- El experimento que antecedió a la teoría
- 6: Los diagramas espacio-tiempo de Minkowski
- 7: Las transformaciones de Lorentz
- 8: Representaciones matriciales
- 9: Suma relativista de velocidades
- 10: Una teoría libre de asimetrías y de paradojas
- 11: El efecto Doppler relativista
- 12: Dinámica relativista
- 13: La ecuación más famosa de Einstein
- 14: Física atómica relativista
- 14: Invariantes
- Rotaciones y transformaciones
- 15: Los 4-vectores I
- Los 4-vectores II
- El germen de una idea
- 17: El principio de equivalencia
- 19: Predicciones, confirmaciones, y reflexiones
- 20: Introducción al cálculo tensorial
- 22: Tensores de orden superior y mixtos
- 23: Aritmética de tensores
- Propiedades de los tensores
- 24: El tensor métrico
- Gimnasia de índices
- La derivada covariante de un tensor I
- La derivada covariante de un tensor II
- La derivada covariante de un tensor III
- La derivada covariante de un tensor IV
- El determinante del tensor métrico
- La divergencia de un tensor I
- La divergencia de un tensor II
- Electrodinámica relativista I
- Electrodinámica relativista II
- El tensor energía-tensión
- Electrodinámica relativista III
- La ruta geodésica I
- La ruta geodésica II
- La ruta geodésica III
- El transporte paralelo
- La derivada absoluta
- El tensor de Riemann I
- El tensor de Riemann II
- La ecuación de desviación geodésica
- La geometría Euclideana y la Relatividad
- Los tensores de Ricci y Einstein I
- Los tensores de Ricci y Einstein II
- Orbitas planetarias relativistas
- La reducción a los límites clásicos
- La solución de Schwarzschild I
- La solución de Schwarzschild II
- La solución de Schwarzschild III
- El abandono de la "accion a distancia"
- Los agujeros negros: Génesis
- 28B: Los agujeros negros estáticos
- 28C: Los agujeros negros dinámicos
- 28D: Los agujeros negros: Evaporación
- 28E: Los agujeros negros: Entropía generalizada
- 28F: Radiación gravitacional
- Cosmología relativista I
- Cosmología relativista II
- 29A: Axiomatización de la Teoría Relativista
- Las escalas de Planck
- El puente Einstein-Rosen
- Cosmología Cuántica
- Perspectivas futuras
- Bibliografia
- Enlaces Wikipedia
- A1: El papel original de Einstein de 1905
- A2: La ecuación de onda electromagnética
- A4: Relatividad General: Manuscritos originales
- A5: La ecuación de onda relativista de Dirac
- A6: Programas de simulación computarizada
-
▼
marzo
(77)