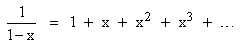todo parecería suponer que, a gran escala, la explicación de la evolución del Universo desde sus inicios radica por completo en una aplicación inteligente de las ecuaciones de campo de la Relatividad General. El problema es que, de acuerdo con lo que se conoce como el teorema de la singularidad, si las ecuaciones de campo de la Relatividad General son válidas, entonces debe de haber una singularidad ya sea en el pasado o en el futuro del Universo, y en esa singularidad las ecuaciones de campo ya no pueden ser utilizadas. De este modo, la Relatividad General provoca su propio colapso, porque predice que no puede predecir la evolución del Universo de principio a fin.
Ha habido un esfuerzo intenso por tratar de explicar lo que ocurre a escala macrocósmica no en base a lo que se aplica a lo extremadamente grande, la Relatividad General, sino en base a lo que rige a lo extremadamente pequeño a niveles atómicos y sub-atómicos, la Mecánica Cuántica.
¿Cómo es posible que se trate de explicar matemáticamente lo que ocurre a escalas astronómicas usando para ello las reglas que rigen a lo que ocurre a escalas sub-atómicas, proyectando matemáticamente lo casi infinitamente pequeño con lo casi infinitamente grande?, dirán algunos. Esto parecería en primera instancia una exageración de los teóricos, porque las leyes que rigen al cosmos a gran escala parecen tener muy poco o nada que ver con las leyes que rigen al mundo sub-atómico. Las ecuaciones y los conceptos son totalmente diferentes. Sin embargo, si hemos de aceptar en su totalidad los modelos cosmológicos que nos proporcionan las ecuaciones de campo de la Relatividad General, necesariamente tenemos que aceptar la existencia de un Universo dinámico que se está expandiendo o contrayendo, no habiendo duda alguna ya de que se ha estado contrayendo, y extrapolando los datos hacia atrás llegamos a la conclusión inevitable de que al momento de su nacimiento el Universo no era el gran cosmos que vemos hoy sino algo inmensurablemente pequeño, algo en lo que aplican las leyes que rigen a las partículas sub-atómicas. Entonces, a un infinitésimo de su nacimiento, el Universo estaba regido en su totalidad por las reglas que rigen hoy a la Mecánica Cuántica, en una época en la cual la Relatividad General y la Mecánica Cuántica estaban completamente unificadas, y conforme fue evolucionando el Universo necesariamente tendrían que haber estado en acción las leyes para la evolución de un sistema físico que rigen en la Mecánica Cuántica. Siendo así, no suena tan disparatada la idea de intentar encontrar una explicación a todo lo que hoy vemos tomando como base lo que se ha comprobado que funciona para predecir correctamente desde la Tabla Periódica de los Elementos hasta el electromagnetismo de las partículas sub-atómicas. Esto es lo que nos lleva a una área de estudio contemporánea conocida como la Cosmología Cuántica.
Puesto que en la Mecánica Cuántica basada en las “ondas de materia” el punto de partida tradicional ha sido la ecuación de onda de Schrödinger, describiéndose el comportamiento de una partícula sub-atómica en base a su función de onda ψ (la gran mayoría de los científicos han dejado ya de tratar de averiguar qué es exactamente lo que está “ondulando”, aceptando la interpretación de Copenhague que impone límites a lo que podemos saber acerca de lo que está ocurriendo en el mundo sub-atómico, y aceptando a ψ como un mero artificio matemático útil que nos sirve para obtener fórmulas, explicaciones y resultados que concuerdan con las evidencias experimentales recabadas), no nos debe asombrar el que uno de los primeros intentos de extender a la Mecánica Cuántica hacia el Universo entero haya consistido en la búsqueda de una función de onda para el Universo. Esto ocurrió con la publicación en 1967 de lo que hoy conocemos como la ecuación Wheeler-De Witt, previamente llamada ecuación Einstein-Schrodinger. La ecuación Wheeler-De Witt es lo que obtenemos cuando llevamos a cabo lo que se conoce como Mecánica Hamiltoniana en el espacio-tiempo de la Relatividad General. El Hamiltoniano en sí que corresponde a esta ecuación termina convirtiéndose en una expresión que debe ser igual a cero, conocida como la constricción de Hamilton. Fue hasta el año 1983 cuando se publicó en el Physical Review una solución a la ecuación Wheeler-De Witt en un trabajo titulado “Wave function of the universe”, elaborada por James Hartle y Stephen Hawking, solución hoy conocida como el estado Hartle-Hawking, la cual tenia como intención original ser una propuesta para la función de onda del Universo. Estos primeros intentos sentaron las bases para llevar a la Cosmología Relativista clásica hacia un nuevo terreno al haberse agotado las posibilidades ofrecidas por la Relatividad General actuando por sí sola sin ninguna ayuda de parte de la Mecánica Cuántica.
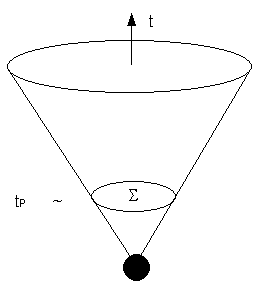
Ya hemos visto cómo la Relatividad General nos describe al campo gravitatorio como deformaciones del espacio-tiempo, concretamente, como una modificación de la métrica, y cómo al que una partícula el campo gravitatorio también puede evolucionar desde una configuración hasta otra, como en el caso de una estrella que explota en supernova, en donde el campo gravitatorio está evolucionando. El espacio de configuraciones de la Relatividad General es el espacio de todas las métricas posibles. A este espacio se lo denomina superespacio. En vez de considerar todas las métricas posibles que son muchas, podemos centrarnos sólo en unas pocas dependiendo del problema que queramos resolver, y hemos visto cómo en cosmología es usual centrarse en las métricas que corresponden con espacios homogeneos e isótropos, es decir, métricas en las que el espacio dentro del espacio-tiempo tiene características iguales en todos los puntos. Estos espacios pueden evolucionar con el tiempo, por ejemplo expandiéndose de acuerdo con la ley de Hubble. Al espacio de configuraciones de estas métricas se lo denomina minisuperespacio. Esto es lo que ha tenido que decirnos la teoría “clásica” basada estrictamente en las ecuaciones de campo de la Relatividad General. En la Mecánica Cuántica el espacio de configuraciones adquiere un papel algo diferente. La partícula ya no se mueve a lo largo de una trayectoria rectilínea, sino que para cada instante de tiempo existe una distribución de probabilidad en el espacio que nos dice dónde encontrar a la partícula con cierta probabilidad. A este distribución de probabilidad se la conoce con el nombre de función de onda. Si encontramos a la partícula en un tiempo determinado en un lugar, luego, en otro tiempo posterior, podemos encontrarla en otro lugar que no corresponde con el que estaría si hubiese seguido una trayectoria clásica. Incluso, la Mecánica Cuántica predice situaciones en las que una partícula que se encuentra frente a una barrera potencial (por ejemplo una fuerza repulsiva que actúa sobre ella, una pared, etc.) puede traspasarla pese a que clásicamente chocaría contra dicha barrera sin poder pasar. Esto es conocido como el efecto túnel:
En la Cosmología Cuántica Canónica, la situación es similar y el efecto túnel adquiere un papel importante. Para entenderlo, se trabaja inicialmente sobre un modelo simplificado en donde aparece este fenómeno de tunelaje, conocido como el espacio-tiempo de de-Sitter. El modelo de de-Sitter resulta cuando se considera un espacio completamente vacío pero con una constante cosmológica. Este modelo es homogeneo e isótropo no solo en el espacio, sino también en el tiempo. Se trata de un modelo en el cual cualquier punto del espacio-tiempo es igual a todos los demás. En otras soluciones cosmológicas con singularidad inicial sólo los puntos de una sección espacial son todos iguales, mientras que los puntos en secciones espaciales diferentes no tienen por qué ser iguales, es decir, no tienen por qué tener características iguales de densidad, curvatura, etc. En el modelo de-Sitter, sin embargo, todos los puntos son iguales. Esto significa que el modelo no presenta una singularidad inicial. Este modelo es de especial interés porque describe una expansión exponencialmente acelerada, tal y como se asume que se dió en lo que se conoce como el periodo inflacionario del Universo, y proporciona, por lo tanto, un modelo descriptivo de esa fase. En la teoría clásica de cosmología el Universo o bien fue de-Sitter siempre, y fue por lo tanto infinito en el pasado (sin singularidad inicial, cosa que no concuerda con nuestra idea actual de universo y mucho menos con las evidencias experimentales recabadas) o bien fue de otro tipo, pero entonces tuvo una singularidad inicial en un tiempo t = 0. Lo que no puede ocurrir en la teoría clásica es que un Universo empiece con una singularidad inicial y luego se convierta en un Universo de-Sitter. Lo sorprendente es que la Cosmología Cuántica Canónica en el minisuperespacio hace posible un modelo del Universo que tiene una singularidad inicial en t = 0, pero que se comporta como de-Sitter un instante después en un tiempo t mayor que 0. El mecanismo involucrado es precisamente el efecto mecánico-cuántico de túnel. La situación aquí es básicamente análoga a la de la partícula que se encuentra frente a un potencial, aunque aquí la noción de potencial es la de un potencial efectivo (una correspondencia matemática) con el que se encuentra el universo en un tiempo t = 0 para “tunelar” hacia el modelo de-Sitter. Esta evolución temporal es una legítima solución a las ecuaciones de la Cosmología Cuántica Canónica.
Para determinar la solución de forma única hay que imponer condiciones iniciales, como es usual en los problemas de la física. Existen dos propuestas se pueden considerar como las más importantes: la propuesta de Hartle y Hawking de la cual ya se ha dado un anticipo arriba, y la propuesta de Vilenkin. De ambas propuestas resultan dos soluciones para la función de onda del Universo que se conocen respectivamente con los nombres de función de onda de Hartle-Hawking y función de onda de Vilekin. Hemos visto que en la Mecánica Cuántica una partícula libre ya no se mueve a lo largo de una trayectoria rectilínea, sino que para cada instante de tiempo la función de onda nos dice dónde encontrar a la partícula con cierta probabilidad. Pues bien, esta idea se puede reformular diciendo que la partícula toma realmente todos los caminos posibles a la vez, cada uno de ellos con cierta probabilidad. Este metodología es lo que se conoce como la formulación de la Mecánica Cuántica basada en la integral de caminos de Feynman:
Bajo este esquema, en la Mecánica Cuántica tradicional calculamos la función de onda para una partícula que comenzó en un estado inicial φ0 y que ha llegado al estado φ integrando sobre todos los caminos posibles que conectan ambos estados:
aen donde S[ρ] es la acción para la trayectoria. Igual que en la Mecánica Cuántica, la Cosmología Cuántica Canónica se puede reformular en términos de la integral de caminos. Ésta formulación permite calcular probabilidades de la transición entre dos configuraciones espaciales determinadas, sumando las probabilidades sobre todas las geometrías del espacio-tiempo intermedias posibles. En la Cosmología Cuántica, un “estado” es una “rebanada” (slice) σ tri-dimensional de un espacio-tiempo cuatri-dimensional, y la función de onda de una partícula es reemplazada por la “función de onda del Universo” φ(σ) que es la amplitud de la probabilidad de que el Universo contenga a σ. La integral dada arriba para una partícula es una integral oscilante que por lo mismo es incapaz de convergir, y es por ello que dentro de la Cosmología Cuántica las integrales de caminos son formuladas sobre un trasfondo de cuatro dimensiones en donde la dimensión temporal es asociada con el número imaginario i = √-1, la cual es a veces referida como un tiempo imaginario precisamente porque involucra el uso de números imaginarios, lo cual permite aplicar el procedimiento matemático conocido como continuación analítica que puede ser utilizado para convertir los resultados expresados en cuatro dimensiones a resultados expresados en tres dimensiones espaciales y una dimensión temporal, en este caso continuando analíticamente el parámetro del tiempo hacia valores imaginarios: t → iτ. Esta transformación cambia la firma de la métrica de (- + + +) a (+ + + +), de modo tal que los caminos resultantes se llevan a cabo sobre un espacio Euclideano en lugar de llevarse a cabo sobre un espacio Lorentziano. Al mismo tiempo, la acción se vuelve imaginaria, lo que nos permite escribir S -> i SE en donde SE es la acción Euclideana.
Antes de proseguir, y para el beneficio de aquellos que no han estado expuestos al concepto de la continuación analítica o que si lo vieron lo han olvidado, aquí se hará un breve resumen de dicho concepto tal y como se enseña en los cursos introductorios de la variable “compleja”. Definimos primero un número complejo como aquél que está formado por la suma dos números, un número real a y un número imaginario b:
a + ib = a + b√-1
Los números imaginarios se pueden representar en un plano bi-dimensional conocido como el diagrama de Argand usando la escala horizontal para representar la parte real y la escala vertical para representar la parte imaginaria, como podemos verlo en el siguiente diagrama en donde se ha representado el número complejo 1+2i:
PROBLEMA: Representar en un diagrama de Argand los siguientes números complejos:
2 + 2i
5 + 3i
3 - 2i
-4
2i
-2 - i
-2 + 4i
-5 + 3i
-4 - 4i
5 + 3i
3 - 2i
-4
2i
-2 - i
-2 + 4i
-5 + 3i
-4 - 4i
La representación de los números complejos sobre el diagrama de Argand es la siguiente:
La variable compleja no es más que una generalización del concepto del número complejo y que por lo mismo no tiene nada de complejo:
z = x + iy
En el diagrama de Argand, la variable compleja se puede representar de la siguiente manera:
Una vez definida la variable compleja, podemos usarla para definir una función de variable compleja como la siguiente:
f(z) = 3 z² - 4 z + 5
Asentados los conceptos anteriores, estamos en condiciones de ver la idea que está detrás del procedimiento de continuación analítica.
Tal y como se discute en el famoso libro de Euclides titulado Los Elementos, una serie de números que va aumentando geométricamente como la siguiente:
Sn = 1 + x + x² + x3 + ... + xn
puede ser expresada también de la siguiente manera:
1 + xSn = 1 + x + x² + x3 + ... + xn + xn+1
1 + xSn = Sn + xn+1
1 + xSn = Sn + xn+1
Despejando para x obtenemos lo siguiente:
Ahora bien, si la magnitud de x es menor que la unidad, la cantidad xn+1 se va volviendo cero (xn+1 → 0) conforme x va aumentando, de modo tal que tenemos así la suma de la siguiente serie infinita:
Fue precisamente utilizando la suma de una serie como esta la forma en la cual Arquímedes evaluó el área encerrada entre una parábola y una línea recta. Posiblemente este sea el primer ejemplo de una función que está asociada a la suma de una cantidad infinita de términos. A modo de ejemplo, si hacemos x igual a 1/2, la anterior ecuación nos dá:
Existe, desde luego, una diferencia significativa entre la ecuación original y la ecuación simplificada, porque la ecuación original es válida para cualquier valor de x mientras que la ecuación simplificada no lo es. Por ejemplo, si hacemos x = 2 en la ecuación simplificada, obtenemos lo siguiente:
- 1 = 1 + 2 + 4 + 8 + ...
lo cual no es una igualdad aritmética válida porque el lado derecho no converge hacia ningún valor, mucho menos a una cantidad negativa como -1. Esto nos demuestra que una correspondencia entre una función y una serie infinita como la ecuación simplificada de arriba sólo se sostendrá dentro de cierto rango limitado de la variable. Generalmente hablando, una función analítica f(z) definida en términos de una variable compleja z puede ser expandida mediante una serie de potencias en torno a cualquier valor complejo de la variable z recurriendo a una expansión de series de Taylor, lo cual puede ser escrito como:
pero la serie convergirá en la función sólo sobre una región circular del plano complejo centrada en el punto z0 y extendiéndose hacia el polo más cercano de la función (definimos al polo como un punto en el cual la función se nos hace infinitamente grande en virtud de un término que aparece en un denominador que al tener un valor de cero nos dispara el valor de la fracción hasta el infinito). La función f(z) = 1/(1-z) discutida previamente (con la pequeña variante de que hemos convertido a la variable real x en una variable compleja z) tiene un polo en z = 1, de modo tal que el “disco de convergencia” de la serie de potencias en torno al origen (z = 0) tendrá un radio de 1. Esto está representado en el siguiente diagrama de Argand:
La función analítica f(z) = 1/(1-z) puede ser expandida en una serie de potencias en torno a cualquier otro punto en donde la función y sus derivadas sean “bien comportadas”. Las derivadas de f(z) son:
y así sucesivamente. Injertando estos términos en la expresión para la serie de Taylor, obtenemos:
De este modo, la expansión en serie de potencias llevada a cabo con respecto al punto z = 2 viene siendo:
f(2 + z) = -1 + z - z² + z3 - z4 + ...
Cada serie de potencias obtenida de esta manera sigue siendo convergente solo dentro de la región circular del plano de Argand centrada en z0 y extendiéndose hacia el polo más cercano de la función. En el ejemplo que hemos estado viendo, puesto que la función f(z) = 1/(1-z) tiene un polo en z = 1, la serie de potencias con z0 = 2 es convergente únicamente en la región sombreada de la siguiente figura:
Hasta aquí hemos estado hablando únicamente acerca de la función particular f(z) = 1/(1-z) y simplemente hemos demostrado cómo esta función analítica conocida es igual a cierta serie de potencias dentro de ciertas regiones del plano complejo. Sin embargo, en algunas circunstancias nos puede ser dada una serie de potencias que no tiene una forma explícitamente cerrada para la función analítica que representa (en su región de convergencia). En tales casos frecuentemente podemos determinar los valores para la función analítica subyacente para argumentos que están fuera de la región de convergencia de la serie de potencias dada precisamente mediante la técnica de continuación analítica. Para ilustrar esto, supóngase que se nos da la siguiente serie de potencias:
f(z) = = 1 + z + z² + z3 + z4 + ...
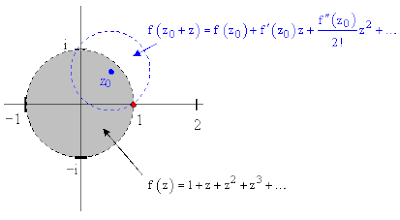
y supóngase que no conocemos la expresión en forma cerrada para la función analítica representada por esta serie. Como se observó arriba, la serie converge para valores de z con magnitudes menores que 1. De cualquier manera, mediante el proceso de continuación analítica podemos determinar el valor de esta función en cualquier valor complejo de z siempre y cuando la función en sí sea bien comportada en dicho punto. Para ello, considérese nuevamente la siguiente región de convergencia para la serie de potencias dada:
Puesto que la serie de potencias conocida es igual a la función dentro de su radio de convergencia, podemos evaluar f(z) y sus derivadas en cualquier punto en dicha región. Podemos, por lo tanto, escoger un punto como el punto z0 mostrado en azul en la figura de arriba, y determinar la expresión en serie de potencias para f(z0+ z) que será convergente dentro de la región circular centrada en z0 y extendiéndose hacia el polo más cercano. De este modo, podemos evaluar la función para valores que queden fuera de la región de convergencia de la serie de potencias original.
Una vez que hemos determinado la serie de potencias para f(z0+ z), podemos repetir el procedimiento seleccionando un punto z1 que esté dentro de la región de convergencia y determinando la serie de potencias para f(z1 + z), que será convergente en una región circular centrada en z1 y extendiéndose al polo más cercano (que viene siendo z = 1 en este ejemplo). Esto está ilustrado en la siguiente figura:
Continuando de esta manera, podemos extender analíticamente la función sobre todo el plano complejo excepto en donde la función sea singular, esto es, en los polos de la función.
En general, dada una serie de potencias de la forma:
f(z) = a0 + a1(z - α) + a2(z - α)² + a3(z - α)3 + ...
podemos expresar a la misma función como una serie de potencias centrada en otro número complejo cercano b tal como:
f(z) = b0 + b1(z - β) + b2(z - β)² + b3(z - β)3 + ...
Para que estas dos series de potencias sean iguales para valores arbitrarios de z, tenemos que igualar los coeficientes de las potencias de z, de modo que tenemos que tener lo siguiente:
a0 - αa1 + α²a2 - α3a3 + ... = b0 - βb1 + β²b2 - β3b3 + ...
a1 - 2αa2 + 3α²a3 - 4α3a4 + ... = b1 - 2βb2 + 3β²b3 - 4β3b4 + ...
a2 - 3α3 + 6α²a4 - 10α3a5 + ... = b2 - 3βb3 + 6β²b4 - 10β3b5 + ...
a1 - 2αa2 + 3α²a3 - 4α3a4 + ... = b1 - 2βb2 + 3β²b3 - 4β3b4 + ...
a2 - 3α3 + 6α²a4 - 10α3a5 + ... = b2 - 3βb3 + 6β²b4 - 10β3b5 + ...
Esto puede ser representado mediante matrices de la manera siguiente:
Multiplicamos ahora ambos miembros de esta ecuación matricial por la matriz de coeficientes del lado derecho obteniendo lo siguiente:
en donde ε = b - a. Esto, desde luego, es equivalente a la aplicación de la expansión en serie de Taylor. Esto parecería excluír cualquier extensión del dominio de la serie de potencias original. Por ejemplo, supóngase que la función original haya sido la serie de potencias para 1/(1 – z) en torno al punto a = 0, de modo tal que los coeficientes a0, a1, … de la serie de potencias fueran todos iguales a 1. De acuerdo con la ecuación matricial anterior, el coeficiente b0 para la serie de potencias sería simplemente:
b0 = 1 + β + β² + β3 + ...
que desde luego converge sólo sobre la misma región que corresponde a la serie de potencias original. Tampoco sería de ayuda el romper la transformación de la serie en pasos pequeños, porque las composiciones de la matriz de coeficientes están dadas por:
Siendo así, el efecto neto de subdividir a ε en n segmentos de tamaño ε/n y aplicando la transformación individual n veces evidentemente es lo mismo que llevar a cabo la transformación en un solo paso. A partir de esto podríamos concluír que es imposible continuar analíticamente la serie de potencias más allá de cualquier punto tal como 3i/2 que tenga una magnitud mayor que 1. Sin embargo, es posible llevar a cabo la continuación analítica de la serie geométrica en virtud de lo que llamamos convergencia condicional. Esto puede ser mejor explicado mediante un ejemplo. Empecemos con la siguiente serie de potencias:
f(z) = 1 + z + z² + z3 + z4 + ...
centrada en el origen. Ciertamente podemos expresar esto como una serie de potencias centrada en el número complejo ε = 3i/4 porque la serie de potencias f(z) y todas sus derivadas son convergentes en dicho punto (que está situado dentro del círculo unitario de convergencia). Por la penúltima ecuación matricial anterior haciendo a0 = a1 = a2 = … = 1, los coeficientes de:
f(z) = b0 + b1(z - ε) + b2(z - ε)² + b3(z - ε)3 + ...
son (aquí usamos el hecho de que i² = -1, i3 = - i, i4 = 1, i5 = i, y así sucesivamente):
Se puede demostrar que los valores absolutos de estos coeficientes son bn = (4/5)n+1. Ahora bien, si tomamos estos como los valores an y aplicamos de nuevo la misma transformación, desplazando a la serie de potencias por otro margen ε = 3i/4, de modo tal que la serie resultante esté ahora centrada en 3i/2, encontraremos que el coeficiente b0 dado por la penúltima ecuación matricial anterior es:
en completo acuerdo con la expresión analítica para la función. Esta serie claramente converge, porque cada término tiene una magnitud geométricamente decreciente. En forma similar podemos calcular los coeficientes de orden mayor para la serie de potencias centrada en el punto 3i/2, el cual está fuera del radio de convergencia de la serie geométrica original centrada en el origen. ¿Pero cómo puede ser esto, podrían preguntarse algunos? Esencialmente hemos multiplicado el vector columna unitario por el vector de coeficiente dos veces, lo cual sabemos que produce el resultado divergente:
Para examinar esto en mayor detalle, llevaremos a cabo la expansión de las cantidades que aparecen en los paréntesis cuadrados de arriba para b0, lo cual nos dá:
Cada renglón individual es convergente, y más aún los renglones convergen hacia valores geométricamente decrecientes, de modo tal que las sumas de los renglones son también convergentes. Sin embargo, si sumamos los valores individuales en las diagonales, obtenemos:
Podemos ver que los términos para b0 son divergentes si los sumamos diagonalmente, pero son convergentes si los sumamos por renglones. En pocas palabras, la serie es condicionalmente convergente, lo cual significa que la suma de la serie depende del orden en el cual sumemos los términos. Lo mismo aplica a las series para los otros coeficientes.
Puesto que los términos de una serie convergente condicionalmente pueden ser reacomodados para darnos cualquier valor que queramos, uno puede preguntarse si la continuación analítica, que está basada tan fundamentalmente en la convergencia condicional, nos puede producir un resultado único. La respuesta es afirmativa, pero sólo porque estipulemos cuidadosamente el procedimiento para transformar los coeficientes de las series de potencias de tal manera que las sumas sean evaluadas mediante renglones y no de otra manera. Este procedimiento está justificado principalmente por el hecho de que nos produce resultados que están de acuerdo con las funciones analíticas explícitas en aquellos casos en los que tales funciones nos son conocidas. Esta es pues la idea general detrás del procedimiento matemático conocido como la continuación analítica.
Regresamos ahora tras la disgresión a la discusión de la integral de caminos que había quedado arriba en puntos suspensivos.
La integral de caminos es amortiguada por un exponencial de decaimiento (con exponente negativo) y convergirá si SE está acotado abajo. En la Cosmología Cuántica, la transformación implica que debemos integrar sobre hojas (manifolds) que tengan una firma Euclideana en lugar de espacios-tiempo Lorentzianos. De este modo, calculamos la función de onda mediante:
en donde M es un 4-espacio Euclideano (al haberse llevado a cabo la transformación indicada hacia un tiempo imaginario) que contiene una rebanada tri-dimensional σ.
Las observaciones astronómicas nos indican que el Universo es grande y suave en una escala global, y por lo tanto el paso natural consiste en estimar la integral para 3-superficies σ que son grandes y suaves. Aunque el llevar a cabo esta integración esté más allá de nuestras capacidades, es posible hacer una estimación de la misma como el exponencial de una “acción efectiva” γ[M]. Podemos pensar de esta “acción efectiva” como si se tratase de una acción con todas las fluctuaciones cuánticas integradas fuera de la misma:
No parece ser muy útil el intentar definir una función (γ) en términos de una integral de caminos sobre una función (SE) que desconocemos. Sin embargo, gracias a la Relatividad General conocemos una expresión aproximada de γ para los espacios grandes. Los términos principales son simplemente aquellos que corresponden a la acción (Euclideana) para la Relatividad General:
en donde g es el determinante de la métrica gµv y R es el escalar de Ricci (R = gµv Rµv). Esta expresión puede ser considerada toscamente como una expansión en series de potencias en el tamaño inverso del espacio, para hojas grandes (a escalas cosmológicas) el campo de la gravedad es el campo dominante y podemos despreciar los términos que representan otros campos. Puesto que esta última ecuación es simplemente la acción para la Relatividad General, su punto estacionario es la solución a las ecuaciones de campo de Einstein que incluyan a la constante cosmológica; en el espacio Euclideano esto es una 4-esfera. Para tales espacios , R = 4λ y:
∫d4x √g = 24 π²/λ²
Insertando esto en la ecuación anterior para la integral de acción nos produce γ = -3π/Gλ. Puesto que la integral de caminos para Ψ(Σ) es igual al exponencial de -γ/h, tenemos:
Si consideramos a λ como un parámetro independiente, esta expresión alcanza un pico infinitamente grande para λ = 0, con lo cual el problema de fijar a la constante cosmológica a un valor cercano a cero parecería resuelto. La explicación que podemos dar a esto es que los Universos en los cuales λ = 0 son los que predominan en la integral de caminos, haciendo preponderantemente probable que la constante cosmológica se desvanezca. Sin embargo, la constante cosmológica no se puede suponer como un parámetro libre. De cualquier modo, la aplicación de la integral de caminos nos abre aquí un nuevo horizonte de investigaciones posibles.
El éxito de las integrales de caminos para describir en el ámbito de la Mecánica Cuántica a la física no-gravitatoria es lo que condujo a los intentos de describir a la gravedad de la Relatividad General mediante integrales de recorrido. La formulación de la gravedad cuántica mediante integrales de camino no está libre de problemas, como tampoco está claro cómo se relaciona con intentos más modernos para construír una teoría de la gravedad cuántica como la teoría de las supercuerdas, mejor conocida últimamente como la teoría-M. Sin embargo, la integral de caminos puede ser utilizada para calcular correctamente cantidades que pueden ser calculadas independientemente de otras maneras, como las temperaturas y las entropías de los agujeros negros.
La propuesta de Vilenkin consiste en tomar como condición inicial una métrica espacial inexistente. Tal estado no tiene correspondencia física alguna en la teoría clásica de la Relatividad General, y fue denominado “nada” por Vilenkin. Este es posiblemente el orígen del mito popular de un Universo creado de la nada. La pregunta sobre el orígen de esta transición se reduce a la misma categoría que la pregunta sobre la razón de que el decaimiento de un átomo ocurra en un instante de tiempo y no en otro o a la pregunta sobre si la partícula cuántica pasará el potencial por medio del efecto túnel o no. Es todo una cuestión de probabilidades, de naturaleza aleatoria en el marco de la física cuántica. Vilenkin ha demostrado que tal probabilidad de transición es máxima para universos con secciones espaciales cerradas en los cuales Ω0 es mayor que la unidad, o sea con una superficie tipo esférica (o elipsoidal) en donde la geometría no-Euclideana hace que los ángulos de un triangulo sumen más de 180°:
En lo que respecta a la propuesta de Hartle-Hawking, esta consiste en tomar como condición inicial el conjunto todas las geometrías Euclideanas compactas posibles, como por ejemplo una 4-esfera (geometrías sin dimensión temporal). Intuitivamente consiste en acoplar el espacio-tiempo en expansión a todas las formas posibles de cerrarlo o redondearlo suavemente, sin picos o singularidades, en su inicio. En palabras del mismo Stephen Hawking: las condiciones de contorno del universo consisten en que el Universo no tiene condiciones de contorno:
La teoría desarrollada en 1983 por Stephen Hawking y James Hartle para una “Función de onda del Universo”, también conocida como la “Teoría de la Propuesta sin Límites“ (No Boundary Proposal Theory) se puede parafrasear del siguiente modo: la condición límite del Universo es que no tenga límite. Sólo si el Universo se halla en ese estado carente de límite, las leyes de la ciencia pueden determinar por sí mismas las probabilidades de cada historia posible, y en este caso las leyes ya conocidas determinan cómo debe comportarse el Universo. Si el Universo se halla en cualquier otro estado, la clase de espacios curvos en la suma de historias incluirá espacios con singularidades. Para determinar las probabilidades de tales historias que incluyan una singularidad sería necesario invocar algún principio diferente a las leyes conocidas de la ciencia, y este principio sería ajeno a nuestro Universo, no podría ser deducido desde el seno de éste. Por otro lado, si el Universo se halla en un estado sin límite, se podría en principio determinar completamente cómo debe comportarse, hasta la frontera marcada por el mismo principio de indeterminación. La propuesta sin límite formula predicciones definitivas sobre el modo en que debe comportarse el Universo. Si estas predicciones no coinciden con las observaciones, cabe llegar a la conclusión de que el Universo no se halla en un estado sin límite. La propuesta sin límite se vuelve así una teoría que puede ser rebatida o desmentida por las observaciones experimentales y reemplazada por otra teoría. Si las predicciones de la teoría Hartle-Hawking no coinciden con las observaciones, entonces se tiene que considerar la existencia de singularidades en la clase de historias posibles. Y sería todo lo que se puede conocer. No se podrían calcular las probabilidades de las historias singulares, ni se podría predecir cómo debe comportarse el Universo. Para Hawking y Hartle esa imposibilidad de predicción no importaría mucho de ocurrir sólo en el principio del Universo, que al fin y al cabo el principio ocurrió hace diez o veinte mil millones de años. Pero sostienen que si la posibilidad de predicción se quebró en los intensos campos gravitatorios del Big Bang, también podría venirse abajo en cualquier parte, hasta en una estrella. Según Hawking y Hartle, si las leyes de la física pudieron quebrarse al principio del Universo, ¿por qué no podrían quebrarse en cualquier parte? En la Mecánica Cuántica, de naturaleza eminentemente probabilística, hay un principio básico: todo lo que no está prohibido puede suceder y sucederá. De este modo, si la clase de historias posibles incluye espacios con singularidades, éstas podrían ocurrir en cualquier parte y no sólo en el principio. Ello significaría que no habría capacidad de predecir nada. De igual modo, el hecho de que no se puedan predecir acontecimientos constituiría una prueba experimental en contra de las singularidades y a favor de la propuesta sin límite.
En las predicciones de la “Teoría de la Propuesta sin Límites” todas las historias posibles del Universo son finitas en magnitud, cualquier cantidad que se utilice como medida del tiempo tendrá un valor máximo y otro mínimo, de modo tal que cada historia estará acotada (bounded).
Así el Universo contará con un principio y un final. El comienzo en tiempo real será la singularidad del Big Bang. Pero en tiempo imaginario ( √-1) el comienzo no será una singularidad. En otras palabras, las leyes de la física se cumplen en todas partes, incluyendo el inicio del Universo. En consecuencia, el acontecimiento que se opte por denominar “comienzo del Universo en tiempo imaginario” será un punto ordinario del espacio-tiempo, muy semejante a cualquier otro. Las leyes de la ciencia regirían en el principio al igual que en cualquier otro momento posterior.
Habiendo eliminado la singularidad inicial en sus consideraciones, Hawking y Hartle partieron en su trabajo asumiendo tomar la integral de caminos solamente sobre métricas no singulares. En el caso de la integral de caminos ordinaria, se sabe que la medida de la misma está concentrada sobre trayectorias no diferenciables. Pero éstas constituyen la terminación, en alguna topología adecuada, del conjunto de integrales de caminos aparejadas con una acción bien definida. De manera similar, se esperaría que la integral de caminos para la gravedad cuántica se tomase sobre la terminación del espacio de métricas parejas. Lo que la integral de caminos no puede incluír son métricas con singularidades cuya acción no está definida.
Como ya se mencionó arriba, por razones prácticas la integral de caminos se formula sobre el soporte de las cuatro dimensiones del espacio-tiempo puestas en igualdad de condiciones, lo cual implica que en vez de hablar acerca de algo como la métrica Lorentziana pura:
- x1² + x2² + x3² + x4²
en donde la primera coordenada es la coordenada del tiempo, estaríamos hablando de algo Euclideano como:
x1² + x2² + x3² + x4²
al poner a x1 = ict con la ayuda de los números imaginarios. Esto nos permite tomar derivadas con respecto a cualquiera de las cuatro coordenadas estando todas en igualdad de condiciones (en inglés se acostumbra llamarle a ésto on an equal footing). Y el procedimiento matemático conocido como continuación analítica nos permite transformar los resultados obtenidos sobre condiciones tetradimensionales en términos de números de tres dimensiones espaciales y una de tiempo. Por ello, a veces se le denomina a la dimensión espacial convertida como de “tiempo imaginario”, porque implica el empleo de cifras imaginarias pero definidas matemáticamente.
Ahora bien, Hawking y Hartle han considerado el uso de la integral de caminos para intentar describir la gravedad cuántica tomando en consideración métricas Euclideanas que carecen de singularidades, con dos alternativas posibles: una métrica Euclideana plana fuera de un conjunto compacto, o una métrica en variedades que son compactas y sin frontera. La primera clase de métricas asintóticamente Euclideanas es sin lugar a dudas adecuada para cálculos de dispersión. Se puede apreciar en la siguiente figura:
que con esta clase de métricas se puede estimar el envío de partículas hacia adentro desde el infinito y observar qué es lo que puede salir hacia el infinito. Todas las mediciones se realizan en el infinito, donde se tiene una métrica de fondo plano, en la cual se pueden interpretar de la manera usual pequeñas fluctuaciones en los campos como partículas. Lo que ocurre en la región de interacción ubicada en el centro se soslaya, esto debido a que se desarrolla una integral de caminos sobre todas las historias posibles para la región de interacción, es decir, sobre todas las métricas asintóticamente Euclideanas.
Pero los estudios cosmológicos habitualmente se realizan con mediciones de regiones finitas. Se procede así, dada la calidad que los humanos tenemos como observadores desde la Tierra. La ubicación de nuestro planeta es en el interior del Universo, lo cual implica tener una posición de observación endógena que no nos permite mirar hacia adentro desde el exterior del Universo con una vista panorámica super-cósmica. Para ver cuál es la diferencia, supongamos primero que la integral de caminos para la cosmología debe tomarse sobre todas las métricas asintóticamente Euclideanas. Esto conlleva a dos contribuciones a las probabilidades para mediciones en una región finita. La primera provendría de métricas Euclideanas conectadas asintóticamente. La segunda provendría de métricas desconectadas que consistieran de un espacio-tiempo compacto que contenga la región de mediciones y una métrica separada asintóticamente:
No se excluyen de la integral de caminos las métricas desconectadas, puesto que a éstas se les puede aproximar mediante métricas conectadas, donde los distintos componentes están unidos por tubos delgados o agujeros de gusano (wormhole) de una acción insignificante. En cuanto a las regiones del espacio-tiempo compactas y desconectadas, estas no afectarían los cálculos de dispersión, ya que no están conectadas con el infinito, lugar en donde se realizan todas las mediciones. Sin embargo, sí afectarán a las mediciones en la cosmología realizadas en una región finita. En efecto, las contribuciones de tales métricas desconectadas predominarán sobre las contribuciones de las métricas Euclideanas conectadas asintóticamente. Aún así, si se supusiese que la integral de caminos para la cosmología pasa sobre todas las métricas asintóticamente Euclideanas, el efecto sería casi el mismo que si ésa pasara sobre todas las métricas compactas. Por lo tanto, parece más naturla hacer que la integral de caminos para la cosmología pase sobre todas las métricas compactas sin frontera, como lo proponen Hawking y Hartle en su teoría de cosmología cuántica. También sugieren ambos que la integral de caminos para la gravedad cuántica debería pasar sobre todas las métricas Euclideanas compactas. Esto se puede traducir como el que el cosmos no tenga ninguna condición fronteriza, lo cual puede ser sostenible dadas las condiciones expansivas, isotrópicas, homogéneas, de las pequeñas perturbaciones que son observadas en el Universo. Por otra parte, se puede considerar que tanto el espectro y las estadísticas de esas perturbaciones han sido observables en las fluctuaciones en la radiación cósmica de fondo. Los resultados obtenidos hasta ahora concuerdan con las predicciones de la proposición de la inexistencia de fronteras. Ello podría constituír a futuro una auténtica prueba de la proposición y de todo el programa Euclideano de gravedad cuántica en cuanto el momento en que las observaciones de las microondas de la radiación cósmica de fondo se extiendan a escalas angulares más pequeñas. Sin embargo, asalta un hecho. Recordemos que la integral de caminos implica la suma de una geometría tetradimensional con una inicial y otra final tridimensionales. La proposición de Hawking y Hartle consiste en abolir las geometrías tridimensionales y sólo incluír una tetradimensional que al final se empareja con las geometrías tridimensionales. El uso aquí de la integral de caminos sólo entrega la probabilidad de un Universo con ciertas probabilidades (el límite de las geometrías tridimensionales) pero creado de la nada o a partir de un algo exótico que en Mecánica Cuántica se le conoce como un instantón. El instantón puede ser utilizado para calcular la probabilidad de transición mecánico cuántica de una partícula a través de una barrera de potencial mediante el efecto tunel señalado arriba, y uno de los ejemplos más sencillos de un sistema con un efecto instanton es el de una partícula situada en uno potencial de dos pozos. En contraste con una partícula clásica cuya energía no es mayor que la energía de la barrera de potencial y por lo tanto es incapaz de atravesar la barrera, existe una probabilidad de que pueda cruzar dicha barrera “por debajo” mediante el efecto túnel, y una forma de calcular esta probabilidad es mediante la aproximación WKB (Wentzel-Kramers-Brillouin) que requiere que el valor de h/2π sea pequeño. La ecuación de Schrödinger para la partícula es:
Si el potencial V(x) se mantiene constante, la solución de esta ecuación vendría siendo una onda plana:
en donde:
Esto nos dice que si la energía de la partícula es menor que la energía potencial, uno obtiene una función que decae exponencialmente. La amplitud asociada de tunelaje es proporcional a:
La integral de caminos nos permite obtener el mismo resultado dándole la interpretación del instanton. Bajo este formalismo, la probabilidad de transición es expresada de la manera siguiente (en el paso intermedio se utiliza la notación de paréntesis angulados bra-ket de Dirac):
Llevando a cabo el procedimiento de rotación Wick que es esencialmente el procedimiento de continuación analítica haciendo la transformación de un marco Lorentziano a uno Euclideano mediante un tiempo imaginario (t → iτ), obtenemos la siguiente representación:
en donde la acción Euclideana SE para la integral de caminos es:
Para el potencial, esto tiene el efecto de darle un giro de 180 grados parándolo de cabeza, haciendo que exhiba dos crestas de energía máxima en lugar de dos pozos. De este modo, a los resultados obtenidos mediante la bien-definida integral de caminos Euclideana se les puede dar una rotación Wick a la inversa para lograr los mismos resultados físicos que serían obtenidos mediante un tratamiento adecuado de la integral de caminos Lorentziana potencialmente divergente. De este modo, el cálculo de la probabilidad de transición para que una partícula pueda tunelar a través de una región clásicamente prohibida (V(x)) mediante una integral de caminos Lorentziana equivale a calcular la probabilidad de transición para tunelar a través de una región clásicamente permitida (con potencial V(X)) mediante una integral de caminos Euclideana (figurativamente hablando, dentro de la perspectiva Euclideana, esta transición corresponde a una partícula rodando de la cima de un potencial de dos pozos parado de cabeza hacia la otra cima del potencial). Esta solución clásica de las ecuaciones Euclideanas del movimiento es justo el ejemplo de un instantón.
En la práctica, el cálculo de las probabilidades dentro de la Cosmología Cuántica utilizando la integral de caminos completa es extremadamente laborioso, y se vuelve necesario utilizar cierto tipo de aproximación conocida como aproximación semi-clásica porque su validez está situada entre la validez de la física clásica y la validez de la Mecánica Cuántica. En esta aproximación semi-clásica uno argumenta que la mayor parte de las cuatro geometrías dimensionales que ocurren en la integral de caminos darán contribuciones muy pequeñas a la integral de caminos y por lo tanto pueden ser ignoradas. De este modo, la integral de caminos puede ser calculada considerando unas cuantas geometrías que son las que dan una contribución particularmente grande a la misma. Estas contribuciones son las que obtenemos precisamente mediante los instantones.
Hay varios tipos de instantones que pueden ser considerados como candidatos para suministrar las condiciones iniciales en el Universo real. El mismo Hawking junto con Ian Moss intentaron describir el inicio del cosmos sobre el supuesto de un Universo cerrado, de geometría tridimensional, y con una eterna inflación. Si el Universo es abierto o cerrado es, por ahora, una interrogante sin una respuesta categórica. En el caso de un Universo plano, la geometría espacial a gran escala es semejante a la del espacio tridimensional de nuestro entorno. Por el contrario, la superficie de las secciones espaciales de un Universo real cerrado se asemejaría a tridimensionales esferas finitas de gran radio. Una geometría abierta se parecería a un hiperboloide infinito. Por lo tanto, para que el Universo sea finito, debe de ser un Universo cerrado. Esto, por ahora, no es lo que estamos viendo. Hay importantes evidencias observacionales que están apuntando hacia una cosmología abierta e infinita para el Universo. Esto dá lugar a una pregunta: ¿existen en ese tipo de espacios cósmicos instantones que puedan describir la creación de universos abiertos? Un posible instanton podría ser la propuesta que hicieron en el año 1987 los físicos Sidney Coleman y Franck De Luccia, quienes propusieron que la materia que detonó el inicio del Universo se encontraba en un estado conocido como “falso vacío” (false vacuum), el cual en términos clásicos es un estado excitado y estable y en Mecánica Cuántica es un estado inestable. Según la Mecánica Cuántica, la materia que se encuentra alojada en un falso vacío puede transferirse a un estado de verdadero vacío. La evolución de un Universo a partir de un instanton Coleman-De Luccia suele ser representada pictográficamente de la siguiente manera:
De acuerdo a Coleman y De Luccia, la transferencia cuántica de la materia en el Universo primigenio procedió vía la formación de núcleos de burbujas alojadas en un falso vacío cuya materia en descomposición se transcurrió hacia el vacío verdadero. En esta proposición, sorprendentemente se puede llegar a consignar que el interior de cada burbuja corresponde a un Universo abierto e infinito en el cual se puede dar la inflación cósmica. Este modelo corresponde a un Universo abierto que cosmológicamente se le conoce como instanton Coleman-De Luccia.
Una propuesta alterna al instanton Coleman-De Luccia fue la presentada por Stephen Hawking y Neil Turok, los cuales propusieron una clase de instanton que da lugar a un Universo abierto, semejante al propuesto por Coleman y De Luccia, pero sin el requisito de un falso vacío y de un estado de excitación para la materia inicial. Esta propuesta suele ser representada pictográficamente de la siguiente manera:
La desventaja de la propuesta hecha por Hawking y Turok es el hecho de que sus instantones tienen singularidades en aquellos lugares en donde la curvatura del Universo se hace infinita, singularidades en donde dejan de funcionar las leyes de la física.
Hay situaciones en las cuales tenemos dos teorías diferentes que pueden explicar lo mismo y predecir el mismo comportamiento de un sistema físico, siendo ambas correctas. Tal es el caso con la Mecánica Hamiltoniana y la Mecánica Lagrangiana. Pero hay otras situaciones en las cuales tenemos dos teorías esencialmente incompatibles en las cuales sólo una de ellas puede ser cierta, o quizá ninguna de las dos. Tal es el caso de la teoría de los instantones de Coleman-De Luccia y los instantones Hawking-Turok. Las diferencias entre ambas teorías son de una naturaleza tal que necesariamente una de ellas tiene que ser una teoría falsa. Pero también es posible que ambas teorías estén erradas, máxime que ambas fueron formuladas en ausencia de una teoría de la gravedad cuántica que, de existir, sea la verdadera teoría, la teoría de la cual se puedan derivar como casos especiales la Relatividad General para explicar los fenómenos del macrocosmos y la Mecánica Cuántica para explicar los fenómenos del microcosmos.
Hablando en términos generales, la Cosmología Cuántica puede ser considerada como una ciencia apenas en ciernes en la cual se han dado los primeros pasos, y muchos trabajos y esfuerzos seguramente tendrán que ser descartados en el camino al darnos cuenta de que alguno de sus postulados o conclusiones estaba esencialmente errado. Sólo el futuro y los posibles avances tecnológicos que pueda tener en el futuro la humanidad podrán decidir cuál de todas las teorías para explicar el origen del Universo es la Cosmología Cuántica correcta, si es que hay una que pueda ser formulada por seres humanos.