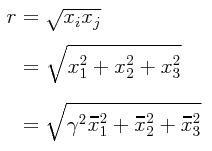Aunque este tema correponde más bien a la Teoría Especial de la Relatividad que a la Relatividad General, se ha puesto aquí siguiendo no sólo la metodología pedagógica que indica que los temas deben ser puestos en orden ascendente de dificultad sino tomando en cuenta el hecho de que el tratamiento del tema requiere de un conocimiento previo del análisis tensorial que no se acostumbra dar en un curso introductorio de la Teoría Especial de la Relatividad pero que es mandatorio antes de entrar de lleno en el tema de la Relatividad General. Este tema requiere de cierta familiaridad con las nociones básicas del electromagnetismo.
El tensor de Faraday F tiene otras aplicaciones además de las que ya hemos visto previamente. Una de ellas consiste en utilizarlo para definir dentro del ámbito de la electrodinámica clásica la densidad de fuerza de Lorentz o 4-fuerza electromagnética de Minkowski f β de la siguiente manera:
Esta definición se basa en la definición del siguiente 4-vector (contravariante) densidad de corriente J:
J = (Jα) = (cρ, J) = (cρ, Jx, Jy, Jz)
Puesto que es la expresión covariante del tensor J la que es utilizada en la definición de la densidad de fuerza de Lorentz, necesitamos bajar el índice con la ayuda del tensor métrico g que corresponde a la métrica de la Teoría Especial de la Relatividad:
(Jα) = (gαμJμ) = (cρ, - Jx, - Jy, - Jz) = (cρ, - J)
PROBLEMA: Demostrar que la densidad de la fuerza Lorentz es igual a un 4-vector con los siguientes componentes temporal y espacial:
Para β = 1 (componente temporal) la definición de la fuerza de Lorentz nos proporciona lo siguiente:
Puesto que F11 (puesto en rojo) es igual a cero, ello nos deja únicamente tres términos cuya substitución nos resulta en lo siguiente:
Para β = 2 (primer componente espacial) la definición de la fuerza de Lorentz nos proporciona lo siguiente:
Substituyendo valores y haciendo uso de la definición del producto cruz de dos vectores, tenemos entonces:
Procediendo de idéntica manera, obtenemos las otras dos componentes espaciales de f β que resultan ser:
Juntando los cuatro resultados obtenidos obtenemos así la expresión que deseábamos demostrar para la 4-densidad de fuerza de Lorentz.
Hablando en términos generales, las fuerzas dinámicas, las fuerzas en movimiento, no tienen cabida dentro de la Teoría de la Relatividad, y esto se aplica no solo a la atracción de la gravedad que es generada no como resultado de una fuerza de atracción de un cuerpo sobre otro sino como resultado del campo con el cual un cuerpo genera en torno suyo una curvatura en el espacio-tiempo; se aplica también a los fenómenos eléctricos y magnéticos. Quizá la ley más básica que podamos encontrar en la electroestática es la ley de Coulomb, pre-relativista, que nos dice en similitud con la ley de gravitación universal de Newton: “dos cuerpos cargados eléctricamente se atraen en proporción directa del producto de sus cargas y en razón inversa del cuadrado de la distancia que los separa”. Esta ley, expresada matemáticamente en unidades del sistema MKS (metro-kilogramo-segundo) tiene la siguiente forma:
El problema esencial con la ley de Coulomb, al igual que el problema con la ley de la gravitación universal de Newton, es que están basadas en el concepto de la “acción a distancia”, el cual supone que entre dos cuerpos que están separados una distancia que (teóricamente) podría ser medida en miles de millones de kilómetros existe una fuerza invisible que los conecta instantáneamente. En principio, si uno de los cuerpos es alejado del otro, la fuerza entre ambos cambia instantáneamente, sin que el límite natural impuesto por la velocidad de la luz presente obstáculo alguno para la “acción a distancia” instantánea. En la ley de Coulomb no aparece la velocidad de la luz, e inclusive ni siquiera aparece el tiempo como factor limitante a la variación de la fuerza de atracción o repulsión electroestática. Esto significa que si ponemos a una carga eléctrica en movimiento sus efectos sobre todas las demás cargas eléctricas del Universo será transmitido instantáneamente, lo cual por sí solo despierta sospechas y dudas.
Las limitaciones impuestas por la ley de Coulomb para el análisis de las cargas eléctricas en movimiento pueden ser superadas con la ayuda de las leyes del electromagnetismo de Maxwell, las cuales son relativísticamente correctas. Esto requiere el abandono definitivo del concepto Coulombiano de la “fuerza eléctrica de atracción o repulsión entre dos cargas eléctricas” substituyéndolo por el concepto del campo generado por dichas cargas. A continuación tenemos dos cargas, una carga positiva de dos unidades (q = +2) y una carga negativa de una unidad (1 = -1), mostrándose los campos eléctricos generados en torno a cada carga y la forma en la que interactúan tratándose de cargas eléctricas de signos opuestos:
En la misma figura se han trazado dos trayectorias, tanto la de una carga positiva que sale disparada (repelida) por la carga eléctrica positiva y que es atraída por la carga eléctrica negativa (trayectoria de color rojo), así como la de una carga negativa que sale disparada (repelida) por la carga eléctrica negativa y que es atraída por la carga eléctrica positiva (trayectoria de color azul). En la siguiente figura tenemos una partícula que sale disparada y repelida con tal fuerza y en tal dirección por la carga positiva que no alcanzará a encaminarse hacia la carga negativa, pudiéndose ver que a lo largo de su trayectoria su vector velocidad (flechita de color verde) no necesariamente será perpendicular a las líneas del campo:
A continuación tenemos dos simulaciones de “fotografías instantáneas” con varias cargas eléctricas de signos diversos cercanas unas a las otras, en las cuales podemos ver la manera en la cual interactúan entre sí los campos de dichas cargas:
Del análisis de las cargas eléctricas puntuales (suponiendo toda la carga eléctrica concentrada en un punto) en movimiento, con la ayuda de las ecuaciones de Maxwell se pueden obtener no sin poco esfuerzo los potenciales Liénard-Wiechert que describen el efecto electromagnético clásico de una carga eléctrica en movimiento en términos de un campo potencial vectorial A y un potencial escalar V. Es importante señalar que los potenciales Liénard-Wiechert preceden a la Teoría de la Relatividad, lo cual explica las dificultades empleadas en obtener clásicamente dichos potenciales a partir de las leyes de Maxwell sin el beneficio de la filosofía relativista.
Para obtener el campo eléctrico E producido por una carga en movimiento, podemos recurrir al procedimiento pre-relativista partiendo de los potenciales Liénard-Wiechert. O podemos utilizar en nuestra ventaja los resultados obtenidos con la ayuda de la Teoría de la Relatividad a través del tensor de Faraday. Ya vimos en una entrada previa que cuando sometemos al tensor de Faraday F a una transformación de Lorentz, los tres componentes del campo eléctrico original E = (E1,E2,E3) y del campo magnético original B = (B1,B1,B3) están relacionados con los componentes de los campos ya transformados E = (E1,E2,E3) y B = (B1,B2,B3) mediante las siguientes relaciones:
E1 = E1___E2 = γ(E2 - βB3)___E3 = γ(E3 + βB2)
B1 = B1___B2 = γ(B2 + βE3)___B3 = γ(B3 - βE2)
B1 = B1___B2 = γ(B2 + βE3)___B3 = γ(B3 - βE2)
De conformidad con la filosofía relativista, en vez de considerar la fuerza eléctrica descrita por ley de Coulomb consideraremos el campo eléctrico E generado por una carga puntual en reposo a una distancia r de dicha carga, definido de la siguiente manera (r es el vector radial, de magnitud variable r):
Estamos interesados en obtener el campo eléctrico generado por esta carga tal y como sería visto por un observador situado en un sistema de referencia S’ en movimiento relativo con respecto al sistema de referencia S dentro del cual la carga eléctrica está en reposo, un sistema que se mueve a una velocidad uniforme V a lo largo del eje-x1 de S. Por conveniencia, consideraremos el campo electrico medido por el observador en S’ cuando los orígenes de ambos marcos de referencia coinciden, y designaremos a este instante t = t’ = 0.
Puesto que una carga eléctrica en reposo no genera campo magnético alguno, B = 0 en el sistema de referencia S, o sea que todas las componentes de B deben ser iguales a cero. Entonces las ecuaciones de transformación de S a S’ nos dicen que debemos tener lo siguiente:
E1 = E1___E2 = γ(E2 - βB3) = γE2___E3 = γ(E3 + βB2) = γE3
En el momento t = t’ = 0, las coordenadas son por transformación inversa de Lorentz:x1 = γx1___x2 = x2___x3 = x3
La distancia radial r del punto de origen en donde está centrada la carga eléctrica al punto de observación (o medición) está dada entonces por la siguiente relación:
De este modo, las componentes del campo eléctrico generadas por la carga eléctrica en movimiento (al estar en el sistema de referencia S’) serán:
o bien, juntando las tres componentes en un solo vector E:
En el sistema de referencia S’ la proyección del vector posición r de la carga en movimiento sobre el eje-x1 será:
x1 = r cos θ
Y del mismo modo:
r² = (x1)² + (x2)² + (x3)²
Entonces:
(x2)² + (x3)² = r² sen² θ
Por lo tanto:
(γx1)² + (x2)² + (x3)² = γ² r² cos² θ + r² sen² θ
(γx1)² + (x2)² + (x3)² = r² [γ² cos² θ + sen² θ]
(γx1)² + (x2)² + (x3)² = r² [cos² θ/(1 - β²) + sen² θ]
(γx1)² + (x2)² + (x3)² = r² [cos² θ + sen² θ - β² sen² θ]/(1 - β²)
(γx1)² + (x2)² + (x3)² = γ² r² [1 - β² sen² θ]
(γx1)² + (x2)² + (x3)² = r² [γ² cos² θ + sen² θ]
(γx1)² + (x2)² + (x3)² = r² [cos² θ/(1 - β²) + sen² θ]
(γx1)² + (x2)² + (x3)² = r² [cos² θ + sen² θ - β² sen² θ]/(1 - β²)
(γx1)² + (x2)² + (x3)² = γ² r² [1 - β² sen² θ]
Con esto, el vector del campo eléctrico de la carga en movimiento resulta ser:
en donde r es un vector radial unitario apuntando radialmente hacia afuera (o hacia adentro) de la carga puntual. Esto lo podemos escribir también de la siguiente manera:
Este es el mismo resultado, pre-relativista, obtenido laboriosamente a partir de los potenciales definidos en partes primero por Alfred-Marie Liénard en 1898 e independientemente por Emil Wiechert en 1900.
Otro resultado que podemos obtener desde la óptica relativista con lo que ya hemos visto es la ley de Biot-Savart que nos proporciona la inducción magnética B producida por un alambre infinitamente largo que transporta una corriente eléctrica:
Clásicamente, para obtener la ley que nos proporciona la magnitud de B a cierta distancia (perpendicular) al hilo conductor, primero subdividimos el hilo en segmentos infinitesimales de longitud:
y llevando a cabo una integración sobre la contribución infinitesimal dB al campo producida por cada elemento infinitesimal de corriente:
B = ∫dB
obtenemos la siguiente expresión:
Para obtener este mismo resultado por la vía de la relatividad, suponemos primero un hilo cargado eléctricamente acomodado a lo largo del eje-x1 de S, de modo tal que la distribución de cargas eléctricas sobre el hilo estará en reposo para un observador situado justo a un lado del hilo en el sistema de referencia S. Pero si ponemos al hilo de cargas en movimiento longitudinal con respecto a nosotros (o bien si nos desplazamos paralelamente al eje a velocidad constante) poniéndonos así en un sistema de referencia S’, entonces para nosotros el hilo tendrá el equivalente real de una corriente eléctrica. Si hay una densidad uniforme de carga lineal ρ a lo largo del hilo en S, entonces en cualquier elemento infinitesimal de longitud dx1 habrá una carga eléctrica ρdx1. De acuerdo con la ley de la conservación de la carga eléctrica, hay una cantidad igual de carga contenida en el intervalo dx1 en un sistema de referencia S que esté en movimiento relativo con respecto a S, con lo cual:
ρ dx1 = ρ dx1
Puesto que en el sistema de referencia S no hay campo magnético alguno al estar las cargas en reposo, si tomamos las relaciones dadas arriba:
B1 = B1___B2 = γ(B2 + βE3)___B3 = γ(B3 - βE2)
tenemos entonces:
B1 = B1___B2 = γβE3___B3 = - γβE2
Por lo tanto, el campo magnético dB debido a un elemento de carga móvil ρdx1 en S’ será:
Con las relaciones obtenidas por la vía del tensor de Faraday tenemos entonces:
Usando lo que hemos visto con anterioridad para el caso de una carga eléctrica individual en movimiento, llegamos a lo siguiente:
o bien:
En forma similar a como ocurre en la derivación clásica (pre-relativista) de la ley de Biot-Savart, obtenemos el campo total B integrando esta última expresión sobre la longitud total (infinita) de la distribución de cargas:
B = ∫dB
Llevando a cabo la integración por los procedimientos usuales del cálculo:
En el sistema de referencia S’, la magnitud de la corriente es:
I = ρβc
mientras que la distancia (perpendicular) desde la línea de cargas móviles (el eje x1) hasta un punto a una distancia r0 es:
Combinando lo que hemos obtenido, tenemos entonces la expresión final para B, que es:
B = 2I/cr0
Esta es precisamente la ley Biot-Savart.
Las predicciones hechas por estas leyes, formuladas antes del arribo de la Teoría de la Relatividad, son relativísticamente exactas, y no requieren de modificación alguna que tome en cuenta la velocidad de las cargas, sobre todo para velocidades cercanas a la velocidad de la luz.
Lo que hemos visto ha establecido una conexión entre el electromagnetismo de Maxwell y la Teoría Especial de la Relatividad. Pero no hemos establecido ninguna conexión entre el electromagnetismo y la Relatividad General. Esto lo podemos hacer en cierta forma a través del tensor energía-tensión como lo veremos a continuación.
El tensor energía-tensión T de las ecuaciones de campo de la Relatividad General es extraordinario en el sentido de que incluye todas las energías posibles habidas y por haber: la energía equivalente de una masa, la energía térmica, la energía de rotación, la energía de movimiento lineal, la energía de enlace entre dos átomos, la energía de enlace nuclear; y desde luego, la energía electromagnética. Y si la energía que estamos considerando es energía electromagnética pura, el tensor que empleamos para estos casos es el tensor electromagnético energía-tensión o tensor electromagnético energía-momentum, el cual puede ser definido de la siguiente manera:
Una ligera variante de la fórmula se obtiene llevando a cabo la subida del índice μ como lo indica la contracción de Fμλ con el tensor gαμ, aunque esto nos resulta en la pérdida de la simetría que exhiben los dos términos dentro del paréntesis:
Esta definición está basada en el tensor de Faraday F que ya vimos previamente, y en el tensor métrico conjugado g-1 = (gμν) para el espacio-tiempo Lorentziano definido aquí como ya lo hemos visto previamente:
g11 = 1___g22 = g33 = g44 = - 1
gij = 0___para i ≠ j
gij = 0___para i ≠ j
PROBLEMA: Obtener los componentes del tensor electromagnético energía-tensión T a partir de la definición dada anteriormente.
Empezaremos con el componente T11, para lo cual hacemos las substituciones α = β = 1 en la definición del tensor energía-tensión T para el campo electromagnético:
Puesto que la métrica es diagonal, en el primer término dentro de los paréntesis el único valor de μ para el cual g1μ no será cero es μ = 1. Por otro lado, en el segundo término tenemos la doble contracción FαβFαβ del tensor de Faraday, la cual ya vimos previamente que nos produce la expresión 2(B² - E²). Expandiendo la sumatoria que nos resulta en el primer término de acuerdo con la convención de sumación para índices repetidos, después de haber puesto g11 = 1, tenemos entonces:
A continuación, substituímos cada uno de los elementos tomándolos tanto del tensor de Faraday en su forma contravariante Fαβ como del tensor de Faraday en su forma covariante Fαβ, obteniendo con esto (se recuerda aquí nuevamente que los sub-índices numéricos dados a las tres componentes espaciales tanto del campo elétrico E como del campo magnético B no tienen relación directa con los índices numéricos empleados para identificar a las componentes del tensor electromagnético energía-tensión T, al igual que como ocurre en el caso del tensor de Faraday F):
Simplificando con el hecho de que E·E = E² = Ex² + Ey² + Ez² = E1² + E2² + E3²:
Finalmente llegamos a lo siguiente:
Como se ha destacado con la simbolización en color azul, el componente T11 resulta ser una expresión muy importante que encontramos en los cursos introductorios de la electrodinámica clásica mucho antes de que se tenga conocimiento alguno de lo que es un tensor. Se trata de la densidad de energía del campo electromagnético, la energía del campo electromagnético por unidad de volumen. Esta cantidad puede considerarse como una especie de energía potencial. La cantidad ∫ε dv (una integral volumétrica) es considerada usualmente como la energía del campo electromagnético. El concepto de una energía almacenada en un campo en lugar de residir dentro de una partícula es un concepto básico del campo electromagnético, y se corresponde. El componente T11 se corresponde con lo que ya habíamos visto previamente cuando identificamos el componente T11 en el ámbito de la Relatividad General como la densidad de masa-energía ρ.
A continuación, llevaremos a cabo la evaluación del componente T12 repitiendo los pasos que acabamos de efectuar, haciendo α = 1 y β = 2 en la definición del tensor electromagnético energía-tensión:
Puesto que g12 es igual a cero, se ha destacado de color rojo indicándose así con ello que se llevará a cabo la eliminación del segundo término, dejándonos únicamente con:
Llevamos a cabo la expansión de la sumatoria de acuerdo con la convención de sumación, destacando de antemano los componentes del tensor de Faraday que son iguales a cero:
Substituyendo los valores de cada componente de los tensores de Faraday covariante y contravariante que se requieren en este caso, tenemos lo siguiente:
En la tercera línea se ha efectuado una conversión de los índices numéricos a las coordenadas espaciales Cartesianas para que sea más claro lo que se va a llevar a cabo. La forma del término entre los paréntesis es la misma que la de un producto cruz, cuyos componentes en coordenadas rectangulares referidas a un triplete de vectores unitarios de base i, j y k, tiene la definición usual que se le dá al producto cruz mediante el determinante de la siguiente matriz:
En base a esto, podemos ver que la componente producida por el producto cruz corresponderá al vector ExB que apunta a lo largo de la coordenada espacial x2 = x, o sea:
Procediendo de modo similar, obtenemos las otras dos componentes que corresponden a los elementos espaciales del tensor T colocados a lo largo del primer renglón en su representación matricial, los cuales apuntan a lo largo de las coordenadas espaciales x3 = y y x4 = z respectivamente:
De igual manera, se puede verificar que las tres componentes que corresponden a los elementos espaciales del tensor T colocadas a lo largo de la primera columna son las siguientes:
Para obtener esto último, no es necesario llevar a cabo las evaluaciones detalladas a partir de la definición, porque el tensor electromagnético energía-tensión de la electrodinámica T, al igual que el tensor energía-tensión T de la Relatividad General, es simétrico.
A esto último podemos darle una interpretación física inmediata apelando a la definición del vector de Poynting S, el cual en unidades Gaussianas está dado por la relación:
El vector de Poynting nos expresa el flujo de energía electromagnética a través del espacio libre, y nos proporciona la cantidad de energía electromagnética que está pasando a través de una superficie por unidad de área por unidad de tiempo.
Habiendo determinado las componentes que corresponden al primer renglón y a la primera columna de la matriz que representa al tensor electromagnético energía-tensión, si borramos el el primer renglón y la primera columna de la matriz nos queda una sub-matriz. Esta sub-matriz, con un signo negativo antepuesto, es mejor conocida como el tensor de tensión de Maxwell (Maxwell stress tensor), la cual podemos representar como [TM]. A continuación procederemos a determimar el elemento T23 que corresponde a esta sub-matriz de acuerdo a la definición del tensor completo T dada arriba.
Expandiendo la sumatoria de acuerdo a la convención de sumación:
A continuación, substituímos los componentes del tensor de Faraday covariante y contravariante en esta expresión, pero para evitar una posible confusión de los sub-índices numéricos empleados en la designación de los componentes de E y B con los índices del tensor emplearemos la notación correspondiente a las coordenadas rectangulares Cartesianas:
Procediendo de modo semejante, obtenemos lo siguiente:
Ahora evaluaremos el componente T22 que corresponde a una de las entradas diagonales del tensor tensión de Maxwell:
En el primer término, la expansión de la sumatoria sobre μ sólo es efectiva para μ = 2 en virtud de que para cualquier otro valor g2μ es igual a cero. Sacándolo fuera del paréntesis y substituyéndolo por su valor g22 = -1 tenemos entonces:
Obsérvese con atención que no hemos puesto μ = 2 en el segundo término, en virtud de que los índices no son índices libres sino índices monigote al llevar a cabo la doble sumatoria sobre ambos índices como lo requiere la convención de sumación.
El segundo término nos debe resultar familiar, ya que en un problema anterior se demostró que la expresión FαβFαβ es igual a 2(B² - E²). Substituyendo este resultado y llevando a cabo la sumación en el primer término tenemos entonces:
Substituímos ahora los componentes de los tensores de Faraday covariante y contravariante empleando en los sub-índices de los componentes (espaciales) de los campos E y B la notación usual de coordenadas rectangulares Cartesianas para obtener así:
Puesto que:
B² = Bx² + By² + Bz²
Bx² - B² = - Bz² - By²
Bx² - B² = - Bz² - By²
tenemos entonces:
lo cual podemos simplificar llegando a la siguiente relación:
Procediendo de igual forma, encontramos que los componentes T33 y T44 son los siguientes:
Tenemos ya pues los elementos que forman parte de la sub-matriz 3x3 que constituye el tensor tensión de Maxwell.
No cuesta mucho trabajo verificar que los resultados que acabamos de obtener se pueden obtener también mediante la siguiente fórmula:
en la cual i = 1, 2, 3 y j = 1, 2, 3. Los índices numéricos en esta última fórmula no son los índices del tensor energía-tensión del campo electromagnético, son los índices que corresponden e identifican a los elementos de la representación matricial del tensor tensión de Maxwell.
La selección de componentes a ser utilizados dependerá de cada situación en particular, como lo demuestra el siguiente ejemplo.
PROBLEMA: Construír la representación matricial del tensor tensión de Maxwell para el caso en el cual tenemos un campo eléctrico estático.
En este caso, el campo magnético B = 0 y los elementos de la matriz se reducen a los siguientes:
Los resultados que hemos obtenido para el tensor energía-tensión del campo electromagnético se pueden resumir de la siguiente manera:
De este modo, si tomamos los elementos principales comunes del tensor electromagnético energía-tensión T agrupándolos de acuerdo con el significado común que se les puede dar, tenemos los siguientes cuatro sub-grupos:
En forma similar a como ocurre con el tensor energía-tensión T de la Relatividad General, el elemento Tμν del tensor electromagnético energía-tensión se puede interpretar como el flujo de la μ-componente del 4-momentum P = (Pμ) del campo electromagnético a través del hiperplano xν = constante, y representa la contribución del electromagnetismo a la fuente del campo gravitacional en la Relatividad General.
Podemos representar los sub-bloques de los que consta el tensor electromagnético energía-tensión usando la definición de la densidad del momentum del campo electromagnético g dada en función del vector de Poynting (no se confunda con el símbolo utilizado para representar al tensor métrico):
Con esto, la representación en sub-bloques del tensor T = (Tαβ) es:
Mediante un poco de gimnasia de índices podemos obtener las siguientes representaciones equivalentes del tensor electromagnético energía-tensión:
PROBLEMA: Demostrar que el tensor energía-tensión del campo electromagnético tiene una traza de cero.
La traza del tensor T la obtenemos sumando los elementos de la diagonal principal de su representación matricial (aquí usaremos la convención de sumación con los índices repetidos):
tr {T} = Tμμ
tr {T} = T11 + T22 + T33 + T44
tr {T} = T11 + T22 + T33 + T44
Ya vimos arriba que el componente T11 es ε, la densidad de energía del campo electromagnético, con lo cual:
tr {T} = ε + Tkk
en donde hemos representado (recurriendo nuevamente a la convención de sumación empleando índices repetidos) como Tkk a la suma de los componentes espaciales diagonales del tensor T. Puesto que tenemos que llevar a cabo la suma de T22 + T33 + T44, los agruparemos aquí nuevamente en preparación para la adición de los mismos:
Tenemos entonces:
Haciendo uso del hecho de que:
E² = Ex² + Ey² + Ez²
B² = Bx² + By² + Bz²
B² = Bx² + By² + Bz²
podemos sumar las “columnas” para obtener entonces:
lo cual se reduce finalmente a:
y dado que:
concluímos entonces que:
tr {T} = 0
Con el tensor energía-tensión del campo electromagnético T en nuestras manos, si queremos saber cómo un campo electromagnético puede producir una curvatura en el espacio-tiempo todo lo que tenemos que hacer es substituírlo en las ecuaciones de campo de la Relatividad General. Si el tensor energía-tensión T en cierta región del espacio-tiempo tiene como únicas componentes las que corresponden al campo producido por un campo electromagnético en el espacio libre siendo por lo tanto el tensor electromagnético energía-tensión, entonces las ecuaciones de campo de Einstein son conocidas como las ecuaciones Einstein-Maxwell se pueden escribir en notación de componentes de la siguiente manera (la adición de la la permeabilidad magnética μ0 se ha efectuado aquí con el propósito de que la expresión sea dimensionalmente correcta en el sistema internacional de unidades SI):
Si la constante cosmológica del Universo es puesta igual a cero (Λ = 0) como terminó haciéndolo Einstein, las ecuaciones Einstein-Maxwell se reducen a:
En principio, de acuerdo con esto último y aunque los efectos son insignificativamente minúsculos, el campo electromagnético tiene la capacidad para provocar una curvatura en el espacio-tiempo. Puesto que un fotón de luz es esencialmente un corpúsculo de energía electromagnética, el torrente de fotones con los cuales el Sol está bañando constantemente a la Tierra permitiendo que la vida florezca en nuestro planeta tiene la capacidad para producir en conjunto una pequeñísima curvatura en el espacio-tiempo. En pocas palabras, la luz puede provocar los efectos típicos de una atracción gravitatoria. Esta es una conclusión sorprendente, no prevista por la ley de la gravitación universal de Newton, tomando en cuenta que ni en los tiempos de Newton ni en los tiempos modernos de hoy se considera que el fotón pueda tener masa alguna. A un fotón se le puede asignar una “masa” en función de su energía E = hf y en base a la equivalencia relativista E = mc², pero carece de masa en reposo. Esto significa que, ni más ni menos, algo que carece de masa puede ejercer una atracción gravitatoria a causa de la curvatura que provoca en el espacio-tiempo.