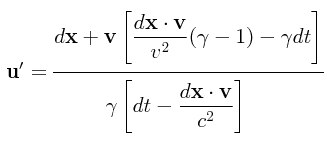La pregunta que nos hacemos ahora es: ¿a qué velocidad verá moverse la pelota un observador situado fuera del tren a un lado de las vías de ferrocarril?
Si pensáramos de acuerdo a la cinemática clásica, diríamos: A la velocidad Vpelota a la que es lanzada la pelota dentro del vagón del tren hay que sumarle la velocidad Vtren a la cual se está desplazando el ferrocarril en el mismo sentido para obtener la velocidad total Vtotal con la cual verá moverse la pelota un observador externo situado a un lado de las vías del ferrocarril, o sea:
Vtotal = Vtren + Vpelota
Pero en la mecánica relativista, este modo de pensar es incorrecto, porque en el ejemplo que se ha puesto arriba una velocidad de la pelota de 200 mil kilómetros por segundo sumada a una velocidad del tren de 200 mil kilómetros por segundo nos daría una velocidad de la pelota de 400 mil kilómetros por segundo para un observador externo, lo cual excede a la velocidad de la luz por 100 mil kilómetros por segundo, violando el principio de que no hay nada que pueda moverse a una velocidad mayor que la velocidad de la luz.
Obviamente, la suma clásica de velocidades tiene que ser modificada. El viajero dentro del tren verá la pelota lanzada por él moviéndose a una velocidad de 200 mil kilómetros por segundo, pero el observador externo no la verá moverse a 400 mil kilómetros por segundo sino a una velocidad menor, ciertamente menor que la velocidad de la luz.
Se puede demostrar que, dentro de la Teoría de la Relatividad, si la velocidad de la pelota dentro del vagón de ferrocarril (en el marco de referencia S') es designada como u' y la velocidad del ferrocarril es designada como v, entonces la velocidad u de la pelota tal y como la verá un observador situado a un lado de las vías será:
Esta relación es conocida también como ley de adición (composición) de velocidades. Pongamos algunos valores numéricos en ésta fórmula. Puesto que la pelota es arrojada dentro del vagón a una velocidad de 200 mil kilómetros por segundo, siendo las dos terceras partes de la velocidad de la luz, podemos escribir u' = 2c/3. Del mismo modo, puesto que el ferrocarril se está desplazando también a una velocidad v de 200 mil kilómetros por segundo, podemos escribir v = 2c/3. Entonces la velocidad de la pelota, vista por un observador externo, será:
u = (2c/3 + 2c/3)/{1 + (2c/3)(2c/3)/c²}
u = (4c/3)/{1 + 4/9}
u = (4c/3)/(13/9)
u = (36/39) c
u = 0.923 c
u = 2,769 kilómetros por segundo
u = (4c/3)/{1 + 4/9}
u = (4c/3)/(13/9)
u = (36/39) c
u = 0.923 c
u = 2,769 kilómetros por segundo
Ahora que tenemos una fórmula para obtener la suma de velocidades en un esquema relativista, podemos recurrir directamente a dicha fórmula para resolver algunos problemas.
PROBLEMA: ¿Cuál será la velocidad de un rayo luminoso lanzado desde una linterna dentro de una nave espacial en la misma dirección en la cual se mueve la nave, para un observador externo que ve a la nave trasladarse a una velocidad u', de acuerdo con la formula relativista para la suma de velocidades?
Poniendo u' = c en la fórmula de arriba, obtenemos:
u' = (u + v)/(1 + vu'/c²)
u' = (c + v)/(1 + vc/c²)
u' = (c + v)/{(c + v)/c)
u' = c
u' = (c + v)/(1 + vc/c²)
u' = (c + v)/{(c + v)/c)
u' = c
El observador externo mide para el rayo de luz la misma velocidad c que la que mide el observador que va dentro de la nave, en concordancia con el segundo postulado de la Teoría Espacial de la Relatividad.
Aunque no es una convención universalmente aceptada, en una buena cantidad de textos se acostumbra simbolizar como u a la velocidad de un cuerpo que se está moviendo dentro de cierto marco de referencia S frente a un observador en reposo situado dentro del mismo marco de referencia:
mientras que la otra forma de simbolizar al movimiento de dicho cuerpo consiste en considerarlo en estado de reposo dentro de un marco de referencia S’ que a su vez está en movimiento relativo frente a otro observador situado en el marco de referencia S, en cuyo caso la velocidad del cuerpo entre ambos marcos es simbolizada como V:
De este modo, en una convención se utiliza un solo marco de referencia S, mientras que en la otra convención se utilizan dos marcos de referencia S y S’. Algunas veces, las velocidades u y V serán iguales, o sea u = V, lo cual describe exactamente la misma situación en ambos casos. En la convención en la cual utilizamos el símbolo V para representar a un cuerpo en reposo dentro de un marco de referencia que se está moviendo con respecto a otro a una velocidad V, ésta convención equivale a anclar el sistema de referencia S’ al cuerpo mismo. En el caso en el que tengamos a un cuerpo moviéndose dentro de un marco de referencia S’ a una velocidad u, el cual a su vez está moviéndose a una velocidad V con respecto a otro marco de referencia S de un observador en reposo, la velocidad del cuerpo medida por el observador en reposo será igual a la suma relativista de velocidades u y V. Cuando no hay confusión al respecto, podemos designar a la velocidad u como V1 y a la velocidad V del marco de referencia como V2 para simplificar así a la suma relativista de velocidades de una manera más general.
PROBLEMA: Un observador en Tierra ve a dos naves espaciales aproximarse en sentido contrario la una a la otra. ¿A qué velocidad debe ir viajando cada nave, suponiendo que ambas tienen velocidades iguales pero en sentido contrario, para que produzcan una suma relativista de velocidades resultante en una velocidad igual a 0.9c?
Llamando V a la velocidad de cada nave con respecto al observador en Tierra, de acuerdo con la fórmula relativista para adición de velocidades tendríamos lo siguiente para lograr una suma relativista de velocidades igual a 0.9 c:
(0.9 c)(1 + V²/c²) = 2V
(0.9)V²/c² - 2V + (0.9/c) = 0
0.9V² - 2Vc² + 0.9 c = 0
(0.9)V²/c² - 2V + (0.9/c) = 0
0.9V² - 2Vc² + 0.9 c = 0
Resolviendo la ecuación cuadrática, encontramos que la velocidad de cada nave espacial debe ser igual a:
V = 0.627 c
PROBLEMA: Tomando la siguiente representación de la fórmula para la adición relativista de velocidades:
demostrar la simetría e integridad de la fórmula despejando a V1 poniéndola en función de V2 y V3 , comprobando que se mantiene el formato correcto para la composición de velocidades.
c²V3 + V1V2V3 = c²V1 + c²V2
c²V1 - V1V2V3 = c²V3 - c²V2
c²V1(1 - V2V3 /c²) = c²(V3 - V2)
V1 = (- V2 + V3)/(1 - V2V3 /c²)
c²V1 - V1V2V3 = c²V3 - c²V2
c²V1(1 - V2V3 /c²) = c²(V3 - V2)
V1 = (- V2 + V3)/(1 - V2V3 /c²)
Este es el mismo formato de la fórmula original, con la substitución:
( V1, V2, V3) → ( V3, - V2, V1)
La fórmula dada para la suma relativista de velocidades es útil para el caso en el cual la persona que viaja en el vagón del tren lanza la pelota en la misma dirección en la cual se está moviendo el tren (el eje de las equis, x). ¿Pero qué relaciones deberán ser aplicadas para el caso en el cual la pelota no es lanzada en la misma dirección en la cual se está moviendo el tren sino en una dirección diferente que involucra las otras dos coordenadas (el eje de las y y el eje de las z)? En tal caso, resulta conveniente derivar unas expresiones de uso general, y para ello podemos recurrir a las ecuaciones de transformación de Lorentz:
____x = γ(x’ + Vt’)
____y = y’
____z = z’
____t = γ(t’ + Vx’/c²)
Por definición, la velocidad instantánea u de un objeto está definida como el cambio infinitesimal en el espacio recorrido ds entre el intervalo infinitesimal de tiempo dt requerido para recorrerlo:
u = ds/dt
En tres coordenadas (x,y,z), las componentes respectivas de la velocidad serán:
ux = dx/dt
uy = dy/dt
uz = dz/dt
uy = dy/dt
uz = dz/dt
Tomando infinitesimales (diferenciales) en cada una de las relaciones de transformación de Lorentz, obtenemos lo siguiente:
dx = γ(dx’ + Vdt’)
dy = dy’
dz =dz’
dt = γ(dt’ + Vdx’/c²)
dy = dy’
dz =dz’
dt = γ(dt’ + Vdx’/c²)
Esto nos lleva directamente a las siguientes relaciones:
PROBLEMA: ¿Cuál es la velocidad de un pulso de luz arrojado en la dirección del eje de las equis de acuerdo con las transformaciones relativistas de velocidad?
En este caso se tiene
u’x = c , u’y = 0 , u’z = 0
Entonces:
ux = {c + V} / {1 + (V/c²)(c)} = c
así como uy = 0 y uz = 0. La luz que se mueve con una velocidad c en el marco de referencia S’ también se mueve con una velocidad c en el marco de referencia S, como lo requiere el segundo postulado de la Teoría Especial de la Relatividad.
PROBLEMA: ¿Cuál es la velocidad de un pulso de luz arrojado dentro del marco de referencia S’ en la dirección del eje-y’ cuando el marco de referencia se está moviendo en dirección del eje-x’ ante un observador externo situado en el marco de referencia S?
En este caso se tiene
u’x = 0 , u’y = c , u’z = 0
Entonces:
ux = {0 + V} / {1 + (V/c²)(0)} = V
uy = {c} / {γ(1 + V(c)/c²) = c/γ
uz = 0
uy = {c} / {γ(1 + V(c)/c²) = c/γ
uz = 0
En este caso, el pulso de luz se desplaza formando un ángulo con respecto al eje de las yes. Este es precisamente el caso que vimos desde un principio cuando un pasajero viajando dentro de un vagón de ferrocarril en su marco de referencia S’ lanzaba un rayo de luz hacia el techo del ferrocarril mientras que un observador externo en su marco de referencia S veía al rayo de luz moverse no verticalmente sino siguiendo una línea recta a lo largo de una pendiente.
Al tenerse ux = V y uy = c/γ, se concluye que en el marco de referencia S la luz viaja a un ángulo α con respecto al eje-y, o sea:
tan α = ux / uy
tan α = γV/c
α = tan -1 (γV/c)
tan α = γV/c
α = tan -1 (γV/c)
Este es justo el ángulo al cual se tendría que inclinar un telescopio para poder mirar una estrella que como resultado de su movimiento orbital alrededor del Sol se está moviendo a una velocidad aparente V encima de nosotros, de lo contrario la estrella no podrá verse. Este fenómeno es conocido como la aberración de la luz de las estrellas distantes:
El fenómeno de la aberración de la luz puede considerarse mejor con el siguiente diagrama que muestra a la Tierra en su movimiento de traslación alrededor del Sol a una velocidad aproximada de 30 mil millas por segundo:
en donde VSE es la velocidad de la estrella con respecto a la Tierra (acercándose), VLS es la velocidad de la luz con respecto a la estrella que suponemos es igual a c, y VLE es la velocidad de la luz con respecto a la Tierra que nos llega de la estrella. Nuestro sentido común nos lleva a creer que la velocidad de la luz con respecto a la Tierra VLE debe ser mayor que la velocidad de la luz con respecto a la misma estrella VLS; esperamos que la velocidad de la luz con respecto a la Tierra deba ser igual a la hipotenusa del triángulo y por lo tanto mayor que c. Pero las observaciones experimentales indican que la velocidad de la luz con respecto a la Tierra también es c, en concordancia con el segundo postulado de la Teoría Especial de la Relatividad.
PROBLEMA: ¿Cuáles son las transformaciones inversas de velocidad para pasar del marco de referencia S al marco de referencia S’ ?
La resolución de este problema requiere simplemente despejar u’x, u’y y u’z de las relaciones para la transformación relativista de velocidades que ya obtuvimos previamente. Esto nos conduce a las siguientes relaciones:
Existen otras maneras de derivar la ley de adición de velocidades, como lo veremos a continuación:
PROBLEMA: Demostrar que dos transformaciones sucesivas de Lorentz en la misma dirección son equivalentes a una transformación sencilla de Lorentz que se lleva a cabo con una velocidad:
Para un marco de referencia desplazándose en la dirección del eje-x a una velocidad V1, las transformaciones de Lorentz para pasar de un sistema S a un sistema S’ se pueden escribir de la manera siguiente:
____x’ = γ1(x + V1t)
____y’ = y
____z’ = z
____t’ = γ1(t + V1x/c²)
Por otro lado, para un marco de referencia desplazándose en la misma dirección a una velocidad V2, las transformaciones de Lorentz para pasar de un sistema S’ a un sistema S’’ se pueden escribir de la manera siguiente:
____x’’ = γ2(x’ + V2t’)
____y’’ = y’
____z’’ = z’
____t’’ = γ2(t’ + V2x’/c²)
Enfocaremos nuestra atención sobre la parte espacial en la coordenada-x de la transformación repetida. Introduciendo los valores de x’ y t’ en la expresión para x’’, tenemos:
x’’ = γ2(x’ + V2t’) = γ2 [γ1(x + V1t) + V2 γ1(t + V1x/c²)]
x’’ = γ1γ2 [x + V1t + V2 (t + V1x/c²)]
x’’ = γ1γ2 [x + V1V2x/c² + V1t + V2t]
x’’ = γ1γ2 [(1 + V1V2/c²) x + (V1 + V2) t]
Sacando fuera de los paréntesis cuadrados el término (1 + V1V2/c²) tenemos:
Llevaremos a cabo una simplificación del factor que tenemos fuera de los paréntesis cuadrados sin olvidar que:
definiéndolo todo dentro de un factor gamma compuesto:
Este factor gamma compuesto siempre será mayor que la unidad, puesto que el numerador 1 + V1V2/c² es mayor que 1 y puesto que para β1 y β2 diferentes de cero el numerador del gamma compuesto será menor que la unidad, garantizando un gamma compuesto mayor que la unidad en todos los casos.
Con esto, la componente espacial a lo largo del eje-x de la transformación repetida de Lorentz resulta ser:
Obsérvese que esta expresión, haciendo V1 = 0 ó V2 = 0, se reduce a la transformación de Lorentz sencilla para la componente espacial.
Definiendo:
entonces la transformación repetida de Lorentz se reduce a:
x’’ = γ(x + Vt)
Vemos que dos transformaciones sucesivas de Lorentz en la misma dirección son equivalentes a una transformación sencilla de Lorentz que se lleva a cabo con una velocidad que es la resultante de la adición relativista de las velocidades V1 y V2 correspondientes a cada transformación original.
Puesto que no hay movimiento relativo alguno aquí entre los ejes-y y eje-z de los sistemas de coordenadas, dichas coordenadas permanecen inalteradas al pasar de un sistema de referencia a otro.
Falta comprobar si la conclusión que obtuvimos sigue siendo válida para la parte temporal de las transformaciones repetidas. Introduciendo los valores de x’ y t’ en la expresión para t’’, tenemos:
t’’ = γ2(t’ + V2x’/c²) = γ2[γ1(t + V1x/c²) + V2γ1(x + V1t)/c²]
t’’ = γ1γ2[t + V1x/c² + V2(x + V1t)/c²]
t’’ = γ1γ2[t + V1x/c² + V2x/c² + V1V2 t/c²]
t’’ = γ1γ2[(1 + V1V2 /c²) t + (V1 + V2) x/c²]
t’’ = γ1γ2 (1 + V1V2 /c²) [t + {(V1 + V2)/(1 + V1V2 /c²)} x/c²]
t’’ = γ1γ2 (1 + V1V2 /c²) [t + {(V1 + V2)/(1 + V1V2 /c²)} x/c²]
t’’ = γ1γ2[t + V1x/c² + V2(x + V1t)/c²]
t’’ = γ1γ2[t + V1x/c² + V2x/c² + V1V2 t/c²]
t’’ = γ1γ2[(1 + V1V2 /c²) t + (V1 + V2) x/c²]
t’’ = γ1γ2 (1 + V1V2 /c²) [t + {(V1 + V2)/(1 + V1V2 /c²)} x/c²]
t’’ = γ1γ2 (1 + V1V2 /c²) [t + {(V1 + V2)/(1 + V1V2 /c²)} x/c²]
Recurriendo nuevamente a las definiciones dadas arriba:
t’’ = γ [t + Vx/c²]
Vemos que también para la parte temporal dos transformaciones sucesivas de Lorentz en la misma dirección son equivalentes a una transformación sencilla de Lorentz que se lleva a cabo con una velocidad que es la resultante de la adición relativista de las velocidades V1 y V2 correspondientes a cada transformación original. Esto concluye lo que queríamos demostrar dándonos de paso otra manera para obtener la ley de adición de velocidades.
Por simplicidad, hasta aquí hemos considerado en las transformaciones de velocidad marcos de referencia que se están moviendo el uno con respecto al otro a una velocidad V al otro a lo largo del eje común de abcisas, el eje-x, sin movimiento relativo alguno con respecto a los ejes eje-y y eje-z. Entendiblemente, la derivación de las transformaciones de velocidad cuando la velocidad entre ambos marcos de referencia ocurre con una velocidad relativa entre ambos marcos con componentes en los tres ejes coordenados Cartesianos será algo más elaborado. Sin embargo, la derivación de la ley generalizada de composición de velocidades se puede simplificar como lo veremos en el siguiente problema si recurrimos a notación vectorial con la velocidad V simbolizada como un vector V (con letra negrita) con componentes relativos en cada uno de los tres ejes Cartesianos:
V = (Vx, Vy, Vz)
Usaremos además la notación vectorial del producto punto ó producto escalar entre dos vectores:
u · V = (ux, uy, uz) · (Vx, Vy, Vz) = uxVx + uyVy + uzVz
Manejando cantidades vectoriales, estamos mejor preparados para llevar a cabo en forma compacta la derivación del resultado general que estamos buscando.
PROBLEMA: Partiendo de la base de que la transformación generalizada de Lorentz entre dos sistemas de coordenadas S y S’ está dada vectorialmente por las siguientes dos relaciones para los componentes espaciales y para el componente temporal:
demostrar que la ley generalizada para la composición de velocidades está dada por la siguiente fórmula vectorial:
En este problema, debe quedar claro que el vector x en la transformación generalizada de Lorentz se refiere a las tres componentes espaciales de dicha transformación antes de llevarse a cabo la transformación:
x = (x, y, z)
del mismo modo que el vector x’ se refiere a las tres componentes espaciales después de haberse llevado a cabo la transformación:
x’ = (x’, y’, z’)
Al igual que como lo hicimos arriba, tomamos infinitesimales en cada una de las relaciones de la transformación generalizada de Lorentz, obteniendo lo siguiente:
Vectorialmente, la velocidad generalizada u’ en el marco de referencia S’ está dada por la siguiente definición:
Entonces, vectorialmente, dividiendo los diferenciales para ambas expresiones tenemos lo siguiente:
Teniendo en cuenta que en el marco de referencia S:
entonces tras unas cuantas manipulaciones algebraicas todo lo anterior se nos reduce a:
Expandiendo γ = √1 - V²/c² = √1 - β², obtenemos la expresión final dada arriba para la ley generalizada de composición de velocidades.
Además de haber obtenido las transformaciones relativistas de velocidad para un objeto lanzado a una velocidad constante u’ dentro de un marco de referencia S’, podemos obtener también las transformaciones relativistas de las aceleraciones en el marco de referencia S de un objeto que se está acelerando dentro del marco de referencia S’. Todo lo que tenemos que hacer es tomar la derivada con respecto al tiempo de la velocidad, que es la definición matemática de la aceleración:
a = ds/dt
En un sistema Cartesiano de tres coordenadas rectangulares, tenemos tres componentes de la aceleración (a’x , a’y , a’z) para un cuerpo dentro del marco de referencia S’ que corresponden a unas aceleraciones (ax , ay , az) en el marco de referencia S. Por lo tanto:
Es importante tener presente que el marco de referencia S se sigue moviendo siempre a una velocidad constante V. Dicho marco de referencia en ningún momento se está acelerando, porque si empezara a acelerarse entonces la Teoría Especial de la Relatividad ya no sería aplicable. Para el estudio de marcos de referencia acelerados es necesario recurrir a la Teoría General de la Relatividad.