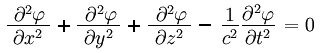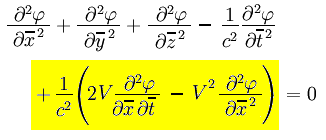Con esta convención, si el objeto ubicado en el punto P empezaba a desplazarse a lo largo de uno de los ejes, digamos el eje y, a una velocidad constante V, digamos de unos 4 metros por segundo, su posición nueva medida a partir de un tiempo t = 0 se podía obtener fácilmente simplemente sumando la cantidad Vt al valor original en dicha coordenada. De este modo, al haber transcurrido un tiempo de t = 3 segundos, el objeto se habría desplazado una distancia de Vt = 12 metros, y sus nuevas coordenadas serían:
x’ = 2 metros (permanece igual)
y’ = y + Vt = 3 metros + (4 metros/segundo) (3 segundos) = 15 metros
z’ = 5 metros (permanece igual)
y’ = y + Vt = 3 metros + (4 metros/segundo) (3 segundos) = 15 metros
z’ = 5 metros (permanece igual)
(Obsérvese cómo se cancelan las dimensiones de las unidades, puestas en color verde, para siempre dar en la respuesta final las unidades correctas. Añadir todas las unidades desde un principio en la solución de cualquier problema matemático, cancelándolas según se requiera, es una buena forma de darse cuenta de que no se están cometiendo errores; llevando la contabilidad correcta de las dimensiones. Si en la respuesta final de un problema un estudiante obtiene metros/segundo cuando esperaba obtener kilogramos por metro cúbico ello le indicará que hubo un error, el cual puede ser corregido de inmediato con sólo ver en dónde fue en donde las unidades se salieron fuera de control.)
De este modo, considerando a dos observadores distintos moviéndose uno con respecto al otro a una velocidad constante V, con un observador O en reposo en su propio sistema de coordenadas rectangulares (x,y,z) al que indistintamente llamaremos también marco de referencia S y otro observador O’ en movimiento junto con su propio sistema de coordenadas rectangulares (x’,y’,z’) al que llamaremos S’, para pasar de un sistema de coordenadas al otro simplemente echábamos mano de las transformaciones de Galileo deducidas como se hizo en el ejemplo de arriba recurriendo a la lógica elemental. Si el movimiento relativo se lleva a cabo a lo largo de un eje común entre ambos, digamos el eje-x, y si suponemos que el marco de referencia S’ es el que se está moviendo de izquierda a derecha:
entonces es fácil ver que las transformaciones de Galileo para pasar las coordenadas de un punto fijo situado en el marco de referencia S’ a las coordenadas que le corresponden en el marco de referencia S deben ser:
x = x’ + Vt’
y = y’
z = z’
y = y’
z = z’
Aunque nos parezca superfluo, por completitud introduciremos el tiempo universal t como un cuarto componente en el conjunto ordenado de componentes de cada sistema de coordenadas. Así, para el observador O un punto cualquiera en su sistema de coordenadas estará especificado como (x,y,z,t), y para el observador O’ otro punto cualquiera en su sistema de coordenadas estará especificado como (x’,y’,z’,t’), y el conjunto completo de transformaciones de Galileo para llevar a cabo la conversión de un punto cualquiera en S’ a las coordenadas que le corresponden en S serán:
x = x’ + Vt’
y = y’
z = z’
t = t’
y = y’
z = z’
t = t’
Hemos supuesto que ambos observadores están provistos de metros y relojes de forma tal que pueden medir las coordenadas de los eventos o acontecimientos que les toque presenciar. Hemos supuesto también que ambos ajustan sus relojes de modo tal que cuando pasen el uno frente al otro en x = x’ = 0 la lectura en sus relojes será t = t’ = 0. El uso de las transformaciones de Galileo quedará más claro con la resolución de los siguientes problemas.
PROBLEMA: Las coordenadas de un punto fijo en el marco de referencia móvil S’ son (x’,y’,z’,t’) = (4,7,2,0). ¿Cuáles serán las coordenadas del mismo punto evaluadas en el marco de referencia estacionario S para un tiempo t = 3 segundos y para un tiempo t = 5 segundos si la velocidad relativa entre ambos marcos de referencia es igual a V = 4 metros/segundo?
Para un tiempo de t’ = 3 segundos, las coordenadas en S se obtienen como:
x = x’ + Vt’ = 4 metros + (4 metros/segundo)(3 segundos) = 16 metros
y = y’ = 7 metros
z= z’ = 2 metros
t = t’ = 3 segundos
y = y’ = 7 metros
z= z’ = 2 metros
t = t’ = 3 segundos
Las coordenadas en S serán entonces (x,y,z,t) = (16,7,2,3).
Para un tiempo de t’ = 5 segundos, las coordenadas en S se obtienen como:
x = x’ + Vt’ = 4 metros + (4 metros/segundo)(5 segundos) = 24 metros
y = y’ = 7 metros
z = z’ = 2 metros
t = t’ = 5 segundos
y = y’ = 7 metros
z = z’ = 2 metros
t = t’ = 5 segundos
Las coordenadas en S serán entonces (x,y,z,t) = (16,7,2,3).
Obviamente, conforme avanza el tiempo, la posición del punto fijo en S’ se va desplazando más y más hacia la derecha. Las coordenadas en el eje-y y en el eje-z se mantienen iguales puesto que no hay movimiento alguno fuera del que se lleva a cabo a lo largo del eje de las equis.
Hemos considerado en la resolución del problema anterior que el marco de referencia S’ es el que se está moviendo de izquierda a derecha (en el sentido positivo del eje-x) a velocidad V, pero la resolución del problema hubiera sido exactamente la misma si hubiéramos considerado al observador O’ fijo y al marco de referencia S moviéndose de derecha a izquierda en el sentido del eje-y:
Para pasar del marco de referencia S al marco de referencia S’, las transformaciones de Galileo serán:
x’ = x - Vt
y’ = y
z’ = z
t’ = t
y’ = y
z’ = z
t’ = t
Obsérvese el cambio de signo que se tuvo que hacer, ya que esta es una transformación inversa a la anterior.
PROBLEMA: Las coordenadas de un punto fijo en el marco de referencia móvil S son (x,y,z,t) = (3,1,8,0). ¿Cuáles serán las coordenadas del mismo punto evaluadas en el marco de referencia estacionario S’ para un tiempo t = 5 segundos y para un tiempo t = 10 segundos si la velocidad relativa entre ambos marcos de referencia es igual a V = 2 metros/segundo?
El punto fijo se encuentra ahora en el marco de referencia S. Para un tiempo de t = 5 segundos, las coordenadas en S se obtienen como:
x’ = x - Vt = 3 metros - (2 metros/segundo)(5 segundos) = -7 metros
y’ = y = 1 metro
z’ = z = 8 metros
t’ = t’ = 5 segundos
y’ = y = 1 metro
z’ = z = 8 metros
t’ = t’ = 5 segundos
Las coordenadas en S serán entonces (x,y,z,t) = (-7,1,8,5).
Para un tiempo de t = 10 segundos, las coordenadas en S se obtienen como:
x’ = x - Vt = 3 metros - (2 metros/segundo)(10 segundos) = -17 metros
y’ = y = 1 metro
z’ = z = 8 metros
t’ = t = 10 segundos
y’ = y = 1 metro
z’ = z = 8 metros
t’ = t = 10 segundos
Las coordenadas en S serán entonces (x,y,z,t) = (-17,1,8,10).
Obviamente, conforme avanza el tiempo, la posición del punto fijo en S se va desplazando más y más hacia la izquierda, en el sentido negativo del eje-x.
PROBLEMA: Un pasajero de un tren que se mueve a 20 metros/segundo para frente a un hombre que se encuentra en la plataforma de la estación en un tiempo que para ambos es t = t’ = 0. Diez segundos después de que el tren lo pasa, el hombre de la plataforma encuentra que un pájaro que vuela a lo largo de la vía y en la misma dirección del tren está a 500 metros de distancia. ¿Cuáles son las coordenadas del pájaro determinadas por el pasajero?
Las coordenadas asignadas al pájaro por el hombre en la plataforma de la estación son
(x, y, z , t) = (500 metros, 0, 0, 10 segundos)
Pasando del sistema de referencia S al sistema de referencia S’ y de acuerdo con las transformaciones de Galileo, la distancia x del pájaro al pasajero, medida por éste es:
x’ = x - Vt = 500 metros - (20 metros/segundo) (10 segundos)
x’ = 300 metros
Entonces las coordenadas del pájaro determinadas por el pasajero son:
(x’, y’, z’ , t’ ) = (300 metros, 0, 0, 10 segundos)
Al pasar del marco de referencia S al marco de referencia S’, las transformaciones de velocidad, según Galileo, basadas en incrementos Δ de las coordenadas, serán:
Δx’ = Δx - Δ(Vt) = Δx - VΔt
Δx’/Δt = Δx/Δt - VΔt/Δt___(dividiendo entre Δt)
Δx’/Δt’ = Δx/Δt - V___(Δt = Δt’)
u’x = ux - V
Δx’/Δt = Δx/Δt - VΔt/Δt___(dividiendo entre Δt)
Δx’/Δt’ = Δx/Δt - V___(Δt = Δt’)
u’x = ux - V
Y del mismo modo:
Δy’/Δt = Δy/Δt
Δy’/Δt’ = Δy/Δt
u’y = uy
Δy’/Δt’ = Δy/Δt
u’y = uy
Δz’/Δt = Δz/Δt
Δz’/Δt’ = Δz/Δt
u’z = uz
Δz’/Δt’ = Δz/Δt
u’z = uz
Por otra parte, al pasar del marco de referencia S al marco de referencia S’, las transformaciones de aceleración, según Galileo, basadas en incrementos Δ de las velocidades con respecto a incrementos iguales de tiempo, serán (la velocidad relativa V entre ambos marcos de referencia permanece constante y no cambia con respecto al tiempo transcurrido):
Δu’x/Δt = Δux/Δt - ΔV/Δt
Δu’x/Δt’ = Δux/Δt
a’x = ax
Δu’x/Δt’ = Δux/Δt
a’x = ax
a’y = ay
a’z = az
a’z = az
El hecho de que la aceleración de un cuerpo medida clásicamente tanto por un observador estacionario como por un observador móvil sea la misma implica que las leyes de Newton basadas en la fórmula fuerza igual a masa por aceleración (F = ma) permanecerán las mismas en todos los marcos de referencia al pasar de un marco de referencia a otro, y por lo tanto los experimentos basados en las leyes de la mecánica clásica basadas a su vez en los conceptos del espacio absoluto y el tiempo absoluto no nos sirven para detectar el movimiento absoluto, confirmando lo que ya habíamos visto al principio de esta obra. El movimiento absoluto no se puede detectar a través de experimentos mecánicos. Pero se suponía que se podía detectar a través de experimentos ópticos usando rayos de luz. Para eso estaba el éter, para darnos un marco de referencia universal e inmóvil con respecto al cual era posible concebir el movimiento absoluto. De este modo, la velocidad de la luz, predicha teóricamente mediante las fórmulas del electromagnetismo de James Clerk Maxwell, parecía zanjar de una vez por todas la cuestión sobre el asunto del movimiento absoluto.
PROBLEMA: Considérese una masa M atada a un resorte que se mueve sobre una superficie horizontal sin rozamiento, y la cual cuando el resorte no está estirado ni comprimido se encuentra a una distancia x0 de la pared a la que está anclado el otro extremo del resorte. Clásicamente, la fuerza de tensión F ejercida por el resorte sobre la masa M cuando es estirado a una distancia x de la pared está dada por la relación que nos dice que dicha fuerza es directamente proporcional a la distancia x-x0:
F = -k(x-x0)
Esta fuerza cuando está desbalanceada produce una aceleración sobre la masa M que está dada por la ley de Newton F = Ma (fuerza igual a masa por aceleración). Demostrar que esta fórmula es invariante bajo las transformaciones de Galileo.
Considerando el movimiento de la masa M a lo largo del eje-x, la ecuación del movimiento de la masa determinada por un observador en reposo con respecto a la superficie es:
F = Ma
-k(x - x0) = Max
-k(x - x0) = Max
Usando las transformaciones de Galileo para determinar la ecuación del movimiento encontrada por un segundo observador moviéndose a una velocidad V con respecto al primero:
x = x’ + Vt’
x0 = x’0 + Vt’
ax = a’x
x0 = x’0 + Vt’
ax = a’x
obtenemos la siguiente ecuación del movimiento para el segundo observador:
-k(x’- x’0) = Ma’x
Puesto que la ecuación del movimiento para el segundo observador tiene la misma forma que la ecuación del movimiento para el primer observador, la ecuación del movimiento es invariante bajo las transformaciones de Galileo. Esto confirma que no se puede detectar el movimiento absoluto haciendo experimentos mecánicos con resortes.
En general, se dice que hay invariancia en una ecuación cuando esta presenta la misma forma al ser determinada por dos observadores distintos moviéndose el uno con respecto al otro. En la teoría clásica se supone que las medidas de espacio y tiempo obtenidas por dos observadores están relacionadas por las transformaciones de Galileo.
PROBLEMA: Suponiendo que los sistemas de referencia S y S’ además de estarse moviendo a una velocidad relativa Vx el uno con respecto al otro en el sentido de los ejes x-x’ se están moviendo también a una velocidad relativa Vy el uno con respecto al otro en el sentido de los ejes y-y’ y a una velocidad relativa Vz el uno con respecto al otro en el sentido de los ejes z-z’, ¿cuáles serán las transformaciones de las coordenadas? ¿Cuáles serán las transformaciones de velocidad? ¿Cuáles serán las transformaciones de aceleración?
Puesto que el movimiento relativo Vx es independiente de los movimientos relativos Vy y Vz del mismo modo que el movimiento relativo Vy es independiente del movimiento relativo Vz, la extensión natural de las transformaciones de Galileo hacia un espacio de tres dimensiones serán:
x = x’ + Vx t’
y = y’ + Vy t’
z = z’ + Vz t’
t = t’
y = y’ + Vy t’
z = z’ + Vz t’
t = t’
Diferenciando con respecto al tiempo las transformaciones anteriores obtenemos las transformaciones de velocidad:
ux = u’x + Vx
uy = u’y + Vy
uz = u’z + Vz
uy = u’y + Vy
uz = u’z + Vz
Diferenciando con respecto al tiempo las transformaciones de velocidad obtenemos las transformaciones de aceleración:
ax = a’x
ay = a’y
az = a’z
ay = a’y
az = a’z
PROBLEMA: Suponiendo que las coordenadas de un punto P’ en S’ son (x’, y’, z’) = (7, 4, 9) en un tiempo t = t’ = 0, y que (V’x, V’y, V’z) = (3, 5, -2), ¿cuáles serán las coordenadas de dicho punto en un tiempo t’ = 6?
Las coordenadas en el sistema de referencia S de tres dimensiones serán de acuerdo con los resultados anteriores:
x = x’ + Vx t’ = 7 + (3) (6) = 25
y = y’ + Vy t’ = 4 + (5) (6) = 34
z = z’ + Vz t’ = 9 + (-2) (6) = -3
y = y’ + Vy t’ = 4 + (5) (6) = 34
z = z’ + Vz t’ = 9 + (-2) (6) = -3
Las coordenadas del punto P en el sistema de referencia S serán entonces:
(x, y, z, t) = (25, 34, -3, 6)
La mecánica clásica, construída sobre las columnas del espacio absoluto y el movimiento absoluto, invariante bajo las transformaciones de Galileo, daba lugar a que las ecuaciones de Newton permanecieran iguales al pasar de un sistema de referencia a otro. Era un entorno cómodo, consistente, con el que todos estaban contentos. El único “pero” que se le podía poner a este esquema era que al intentar extender los conceptos de la mecánica clásica al estudio de los fenómenos propios del electromagnetismo (del cual no se sabía casi nada en los tiempos de Galileo y Newton) empezaban a surgir inconsistencias y asimetrías que no se habían visto en el estudio de la mecánica Newtoniana. Si se suponía que era posible medir el movimiento absoluto de todos los objetos del universo con respecto a un simple rayo de luz, el asunto matemático de repente se había vuelto extraordinariamente complejo. Uno de los primeros en darse cuenta de las complejidades matemáticas que se habían venido encima con la suposición del movimiento absoluto basado en el concepto del éter fue un físico alemán de nombre Albert Einstein. Suponiendo el movimiento absoluto como válido, las mismas fórmulas del electromagnetismo de Maxwell tenían que ser revisadas y modificadas para tomar en cuenta los diferentes resultados experimentales que podrían esperar obtener diferentes observadores en movimiento relativo el uno con respecto al otro y por lo tanto en movimientos diferentes con respecto a un rayo de luz. La revisión requería introducir asimetrías en las fórmulas de Maxwell para dar cabida en ellas a observadores privilegiados cuyo estado de reposo absoluto se encontrase en concordancia exacta con la dirección y la velocidad teórica de un rayo de luz. Estas asimetrías no existían en las fórmulas de Maxwell, puesto que dichas fórmulas no situaban a ningún observador en un plano preferencial con respecto al otro, las fórmulas tal y como estaban dadas por Maxwell eran igualmente válidas para todos los observadores sin cambio alguno. Pero con la velocidad de la luz fijada como una vara de medición absoluta con respecto al éter, las fórmulas de Maxwell habían dejado de ser universales, habían dejado de ser simétricas. Uno de los ejemplos más claros de ello lo es la ecuación de onda electromagnética, obtenida de las ecuaciones de Maxwell de la teoría electromagnética y representada en su forma más compacta por la siguiente fórmula:
Esta fórmula en la que el operador Laplaciano (∇) actuando sobre la onda electromagnética φ representa de manera concisa lo siguiente:
se puede expresar en forma más explícita como:
No es difícil demostrar que al aplicar las transformaciones de Galileo a la fórmula anterior, la ecuación toma el siguiente aspecto (se ha utilizado la sobre-línea encima de cada variable en lugar de la comilla para simplificar la notación):
Claramente, esta fórmula es más compleja que la fórmula original. La única manera en la cual ésta fórmula puede simplificarse es haciendo la velocidad V = 0, lo cual significa regresar a la fórmula original válida para un observador que está en reposo con respecto al éter. El observador que está en reposo con respecto al éter siempre tendrá la fórmula más sencilla de todas; es un observador privilegiado. Todos los demás obtendrán fórmulas diferentes. Y esto cubre apenas las asimetrías con las que nos topamos al manipular la ecuación de onda electromagnética. Cualquier otra situación en la que estén involucradas fórmulas en las que basamos experimentos llevados a cabo con rayos de luz (o con ondas electromagnéticas de teléfonos celulares, radio y televisión) adquirirán asimetrías al pasar de un marco de referencia a otro.
Por más que intentó restaurar con parches las ecuaciones de Maxwell que anteriormente mostraban una simetría perfecta, Albert Einstein lo único que encontró en cada nuevo intento fueron más asimetrías y más asimetrías. Simple y sencillamente no había forma alguna de restaurar las ecuaciones de Maxwell a su condición original como ecuaciones independientes del movimiento del observador. Esto llevó a Einstein a cuestionar las mismas bases de lo que entendemos por movimiento absoluto. En su esencia básica, todo movimiento, medido experimentalmente como una velocidad, definida como la distancia recorrida entre el tiempo empleado en recorrer dicha distancia:
presupone necesariamente que tanto la distancia como el tiempo son parámetros físicos absolutos, invariables.
Pero, ¿realmente podemos considerar la distancia entre dos objetos como algo invariable, absoluto? La lógica nos dice que sí, que dos personas que estén paradas la una frente a la otra medirán la misma longitud de un metro. ¿Y dos personas que se están moviendo la una con respecto a la otra, también medirán la misma longitud de un metro para la vara? El fundador mismo de la mecánica clásica, Isaac Newton, nos había afirmado que sí, y esto se había tomado casi como un dogma indiscutible por muchas décadas en reconocimiento al enorme calibre intelectual de Newton, algo que no era fácil de poner en entredicho en base a lo que nos sugiere nuestra propia intuición. Pero Newton fue más allá al afirmar que eso que nosotros llamamos tiempo también es algo absoluto, universal, en el sentido de que dos personas con relojes diferentes en sus manos y en reposo la una frente a la otra medirán el mismo lapso del tiempo que les marcan los relojes que si se ponen en movimiento la una frente a la otra inclusive hasta alcanzar velocidades extraordinariamente altas. Para Newton, la marcha del tiempo era algo universal, invariable, y si la marcha del tiempo era medida con relojes iguales sincronizados con elevada precisión el uno con respecto al otro, ambos deberían obtener los mismos lapsos de tiempo. Esto, el concepto del tiempo absoluto, aunque un poco menos obvio que el concepto de la longitud absoluta, también era tan obvio a nuestra intuición que simple y sencillamente no había razones para cuestionarlo. Pero el problema de aferrarnos a los conceptos de la longitud absoluta y del tiempo absoluto con su consecuencia directa que es el movimiento absoluto se traducía directamente en la destrucción de la simetría universal mostrada por las ecuaciones básicas del electromagnetismo de Maxwell. Podemos, si así lo deseamos, aferrarnos a los conceptos de la longitud absoluta y del tiempo absoluto, y toparnos con las mismas ecuaciones asimétricas para la teoría del electromagnetismo que Einstein trató de remendar inútilmente.
O podemos, aunque nos cueste mucho trabajo hacerlo, y aunque vaya en contra de nuestro más elemental sentido común, prescindir por completo de los conceptos de la longitud absoluta y del espacio absoluto, y con ello del movimiento absoluto.
Esto, desde luego, nos lleva nuevamente a la misma situación en la cual nos encontrábamos desde la perspectiva de la mecánica Newtoniana, de que no es posible determinar quién es el que se está moviendo, definido el movimiento como algo contra lo que se pudiera decir que nos estamos moviendo. Pero tiene una consecuencia matemática extraordinariamente apetecible: todas las asimetrías que habían surgido en las ecuaciones de Maxwell desaparecen casi como por arte de magia, las ecuaciones básicas de la teoría del electromagnetismo retoman su caráter sencillo y universal. Pero para que esto ocurra, es necesario también que uno de los descubrimientos más sorprendentes de Maxwell, la constancia de la velocidad de la luz considerada como una onda electromagnética, permanezca invariable para distintos observadores aunque estén en movimiento relativo el uno con respecto al otro. En pocas palabras, dos o más observadores que se estén moviendo en direcciones diferentes ambos medirán para un mismo rayo de luz la misma velocidad, siendo esta precisamente la velocidad predicha por las ecuaciones de Maxwell. Convencido de que esta era la única salida posible para el enredo, Albert Einstein formuló los dos principios básicos sobre los cuales descansa la Teoría Especial de la Relatividad, conocida también como Teoría Restringida de la Relatividad o simplemente Teoría Restringida por estar limitada a fenómenos físicos en los cuales no hay aceleraciones entre dos observadores distintos sino únicamente movimientos relativos entre el uno y el otro llevándose a cabo a velocidad constante:
(I) El movimiento absoluto no puede ser detectado, porque tal cosa no existe.
(II) La velocidad de la luz es la misma para distintos observadores.
El primer postulado nos confirma que el movimiento absoluto no sólo no puede ser detectado por medios mecánicos, lo cual ya se sabía desde los tiempos de Newton y Galileo, tampoco puede ser detectado por medios ópticos que involucren a la misma luz así como experimentos de índole eléctrica y magnética, y de hecho no puede ser detectado por medio alguno, no puede ser determinado por ningún tipo de experimento de índole alguna que a alguien se le pueda ocurrir ahora o en el futuro.
Y el segundo postulado es irónico porque a la vez que descarta la existencia de la longitud absoluta y del tiempo absoluto, sube a un pedestal privilegiado a un nuevo absoluto de la física, la velocidad de la luz, la cual será la misma e invariable en cualquier parte del universo para cualquier observador.
Estos dos postulados sobre los cuales descansa la Teoría Especial de la Relatividad, tan sencillos como parecen, tienen repercusiones amplias y profundas, siendo causantes de una de las revoluciones intelectuales más profundas e importantes del siglo XX.
Uno de los primeros triunfos inmediatos de la nueva teoría fue que la ecuación de onda electromagnética permanecía invariante al pasar de un sistema de referencia S a otro sistema de referencia S’ o viceversa; o sea que si la ecuación original en el sistema S era:
entonces en el sistema S’ la fórmula obtenida era:
¡Simetría total, por fin!
Obviamente, las transformaciones requeridas para llevar a cabo la conversión de un marco de referencia a otro no podían estar basadas en las transformaciones de Galileo. Se requería un nuevo tipo de transformaciones incorporando los principios de los dos postulados de la Teoría Especial de la Relatividad. Esto se verá posteriormente con mayor detalle.
De este modo, al llevar a cabo experimentos de óptica con rayos de luz, desaparecía la posibilidad de poder detectar el movimiento absoluto con respecto al éter, y con ello desaparecía la necesidad de creer en la existencia del éter, al mismo tiempo que desaparecía el concepto del observador privilegiado. Pero había que pagar un costo por todo esto. De pronto las transformaciones de Galileo perdieron su carácter universal y sólo eran aproximadamente válidas a bajas velocidades (en comparación con la velocidad de la luz). La cinemática clásica tuvo que ser revisada a fondo y puesta al día. Y la dinámica basada en las leyes de Newton era insostenible en caso de no ser modificada adaptándola a los nuevos conceptos.
En su trabajo original, publicado en 1905 en el tomo 17 de la publicación científica Annalen der Physik, cuya página frontal tenemos a continuación:
y en cuyo interior tenemos el trabajo “Zur Elektrodynamik bewegter Korper” (Sobre la electrodinámica de los cuerpos en movimiento) cuya introducción es:
podemos leer lo siguiente:
“Es conocido que la electrodinámica de (James Clerk) Maxwell -como usualmente se entiende en el tiempo presente- cuando se aplica a los cuerpos en movimiento, conduce a asimetrías que no parecen ser inherentes en los fenómenos. Tómese, por ejemplo, la acción electrodinámica recíproca de un imán y un conductor. El fenómeno observable aquí depende únicamente del movimiento relativo del conductor y el imán, mientras que el punto de vista acostumbrado hace una distinción aguda entre los dos casos en los cuales el uno o el otro de estos cuerpos está en movimiento...
“Ejemplos de este tipo, junto con los intentos infructuosos para descubrir cualquier movimiento de la tierra relativo al “medio de luz” (aquí Einstein está haciendo una clara referencia al éter que supuestamente servía como medio de transporte para la luz) sugieren que los fenómenos de la electrodinámica, así como los de la mecánica, no poseen propiedades que correspondan a la idea del reposo absoluto (si el reposo absoluto no puede ser detectado, tampoco el movimiento absoluto). Estos sugieren que, como ya se ha demostrado al primer orden para cantidades pequeñas, las mismas leyes de electrodinámica y óptica serán válidas para todos los marcos de referencia para los cuales las ecuaciones de la mecánica son sostenidos como válidos. Elevaremos esta conjetura (que será llamada de aquí en delante el “Principio de Relatividad”) a la categoría de un postulado, introduciendo también otro postulado, que es irreconciliable sólo en apariencia con el anterior, que la luz es propagada siempre en el espacio vacío con una velocidad definida c que es independiente del estado de movimiento del cuerpo emisor. Estos dos postulados son suficientes para la realización de una teoría simple y consistente de la electrodinámica de cuerpos en movimiento basada en la teoría de Maxwell para cuerpos estacionarios.”
Para beneficio e interés de los lectores, se ha reproducido íntegramente al final de esta obra la traducción inglesa del trabajo original con el cual Einstein dió a conocer al mundo desde Alemania la Teoría Especial de la Relatividad, puesto en el Apéndice I bajo el título “El papel original de Einstein de 1905”.
Bastan pues tan solo dos postulados sencillos, enunciados en unos cuantos renglones, para construír todo nuestro castillo de conocimientos sobre el tema de la Teoría Especial de la Relatividad (Einstein no utilizó el adjetivo “Especial” en su primer trabajo sobre el tema, esto lo incluiría posteriormente). Aquí tal vez podría preguntarse alguien, ¿y por qué razón Einstein hizo referencia posterior a esta teoría como la Teoría Especial de la Relatividad? ¿Acaso estaba concebida para formar parte de un esquema más amplio? ¿Acaso la Teoría Especial de la Relatividad iba a formar parte de una teoría de mayor cobertura, una Teoría General de la Relatividad? ¿Qué es entonces lo que está ausente de la Teoría Especial de la Relatividad?
En efecto, cuando Einstein concibió la Teoría de la Relatividad en su primer formato, supo desde un principio que esta teoría tendría que formar parte necesariamente de un esquema más amplio, sabía que la Teoría de la Relatividad que había formulado no abarcaba algo que había quedado pendiente y que por lo tanto tendría que ser considerada como una Teoría Especial de la Relatividad.
Para saber qué es lo que había quedado ausente, trasladémonos de nuevo al vagón de ferrocarril herméticamente sellado en el que nuestro viajero se encontraba viajando y en el cual trataba de concebir infructuosamente alguna forma experimental con la cual pudiera saber si se estaba moviendo o no. En base a la Teoría Especial de la Relatividad, no existe experimento alguno que le pueda decir al viajero si se está moviendo o no, porque el movimiento absoluto no existe, siempre fue una quimera a la cual fuimos llevados por la forma tan simplificada en la cual opera nuestro sentido común:
Sin embargo, si el tren se acelera o decelera, por muy blindado que esté el tren por dentro el viajero sabe de inmediato que el tren ha cambiado de velocidad por las fuerzas que experimenta de súbito en el interior. Si lleva un reloj de bolsillo consigo colgando de una cadena y el reloj está suelto, la ligera elevación del reloj le indicará claramente que el vagón está experimentando un cambio de velocidad, un cambio susceptible de ser medido experimentalmente con instrumentos de medición:
Esto parecería darle al ocupante del vagón de ferrocarril la condición de ser un observador privilegiado con respecto a todos los demás observadores externos al tren que lo ven pasar rápidamente sobre las vías del ferrocarril, porque mientras los observadores externos se pueden considerar en estado de reposo el viajero en el vagón blindado se puede dar cuenta de cuándo el vagón está cambiando de velocidad. De lo que no puede darse cuenta es si el vagón se está moviendo a una velocidad constante cuando se está moviendo a una velocidad constante, pero indudablemente que sí se puede dar cuenta de cuándo el vagón ha variado la velocidad de su marcha. Esto parece restaurar cierto status de observador privilegiado al viajero que va dentro del vagón. Pero este es un asunto que involucra aceleraciones, cambios de velocidad, no velocidades constantes. Einstein dejó este asunto pendiente por algún tiempo mientras formulaba esa teoría más general que tomara en cuenta el caso de los cambios de velocidad, esa teoría que llegaría a ser conocida como la Teoría General de la Relatividad de la cual la Teoría Especial de la Relatividad es, perdonando la redundancia, un caso especial.